| В условиях нового экономического уклада в основу принятия хозяйственных решений ложится рыночная информация, а обоснованность решений проверяется также рынком в ходе реализации товаров и услуг. Таким образом, начальным пунктом всего цикла предпринимательской деятельности становится изучение потребительского спроса. Рассмотрим некоторые вопросы математического моделирования спроса в маркетинге.
Уровень потребления можно выразить целевой функцией потребления U = U (Y), где вектор переменных Y ≥ 0 включает разнообразные виды товаров и услуг. Свойства этой функции удобно изучать, используя геометрическую интерпретацию уравнения U (Y) = С, где С – параметр уровня целевой функции потребления (в качестве С может выступать, например, доход).
В пространстве потребительских благ уравнению U (Y) = С соответствует поверхность равноценных, или безразличных, наборов благ, которая называется поверхностью безразличия. В частности, если взять две группы товаров, например продукты питания (у1) и непродовольственные товары и услуги (у2), то уровни целевой функции потребления можно изобразить на плоскости в виде кривых безразличия, соответствующих различным значениям величины С. Вид таких кривых представлен на рис. 25.5, где С1 < С2 < С3. Термин «кривые безразличия» часто используется вне зависимости от размерности пространства потребительских благ и от количества групп товаров и услуг.
При моделировании поведения потребителей исходят из того, что при имеющемся доходе и установленных ценах потребители стремятся максимизировать уровень удовлетворения своих потребностей. Пусть в пространстве п видов товаров спрос потребителей выражается вектором Y = (у1, у2, ..., уп), а цены представлены вектором Р = (р1, p2, ..., рn). При величине дохода Z потребители могут выбирать только такие комбинации товаров, которые удовлетворяют бюджетному ограничению 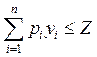 . Тогда простейшая модель поведения потребителей в векторной форме будет иметь вид: . Тогда простейшая модель поведения потребителей в векторной форме будет иметь вид:

Геометрическая интерпретация модели (25.63) для двух агрегированных групп товаров представлена на рис. 25.5. Линия АВ для Z = C1 соответствует бюджетному ограничению и называется бюджетной линией. Выбор потребителей при данном уровне дохода ограничен треугольником А0В. Набор товаров M1, соответствующий точке касания прямой АВ наиболее отдаленной кривой безразличия, является оптимальным решением.
Задача (25.63) в общем случае является задачей нелинейного программирования, с которой связана так называемая функция Лагранжа:
L(Y,λ) = U(Y) + λ(Z – P · Y),
где множитель Лагранжа λ является оптимальной оценкой дохода. Если обозначить частные производные функции U (Y) через Ui: 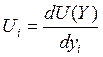 , то эти производные можно интерпретировать как предельные полезности соответствующих потребительских благ, т.е. они характеризуют прирост целевой функции потребления при увеличении использования i-го товара на некоторую условную «малую единицу». , то эти производные можно интерпретировать как предельные полезности соответствующих потребительских благ, т.е. они характеризуют прирост целевой функции потребления при увеличении использования i-го товара на некоторую условную «малую единицу».
Из теории математического программирования известно, что необходимыми условиями того, что вектор Y0 будет оптимальным решением задачи (25.63), являются условия Куна – Таккера:
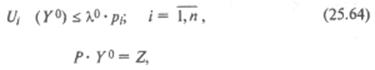
при этом Ui (Y0) = λ0 · рi, если уi0 > 0, т.е. товар приобретается, и Ui (Y0) < λ0 · pi, если уi0 >0, т.е. товар не приобретается.
Из условий оптимальности (25.64) следует, что потребители должны выбирать товары таким образом, чтобы отношение предельной полезности к цене товара было одинаковым для всех приобретаемых товаров:
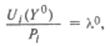
если
Другими словами, в оптимальном наборе предельные полезности выбираемых товаров должны быть пропорциональны ценам.
Функциями покупательского спроса (функциями спроса) называются функции, отражающие зависимость объема спроса на отдельные товары и услуги от влияющих на него факторов. Рассмотрим их построение в зависимости от двух факторов: дохода и цен. Будем в модели (25.63) цены и доход рассматривать как меняющиеся параметры. Тогда решением оптимизационной задачи (25.63) станет векторная функция Y0 = Y0(P, Z), компонентами которой являются на определенный товар от цен и дохода: yi0fi(P,Z).
Рассмотрим частный случай, когда вектор цен остается неизменным, а изменяется только доход. Для двух групп товаров этот случай представлен на рис. 25.5. Если по оси абсцисс отложить количество единиц товара у1, которое можно приобрести на имеющийся доход Z (точка В), а по оси ординат – количество товара y2 той же стоимости (точка А), то прямая линия АВ, называемая бюджетной линией, показывает любую комбинацию количеств этих двух товаров, которую можно купить за сумму денег Z. При увеличении дохода бюджетные линии перемещаются параллельно самим себе, удаляясь от начала координат. Вместе с ними перемещаются соответствующие кривые безразличия.
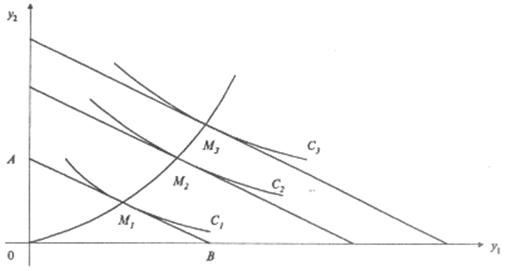
Рис. 25.5. Модель поведения потребителей в графическом виде
Точками оптимума потребительского спроса для соответствующих размеров дохода будут в данном случае точки M1, M2, M3. При нулевом доходе спрос на оба товара будет нулевым. Кривая, соединяющая точки 0, М1, M2, M3, является графическим отображением векторной функции спроса от дохода при заданном векторе цен.
Рассмотрим процесс аналитического построения функций спроса от дохода на основе модели (25.63) на условном примере. Пусть для двух товаров целевая функция потребления имеет вид 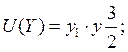 вектор цен Р = (3; 6); величина дохода равна Z. вектор цен Р = (3; 6); величина дохода равна Z.
Так как в данном случае 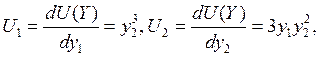 D = Z, то необходимые условия оптимума дают следующую систему уравнений (λ – множитель Лагранжа): D = Z, то необходимые условия оптимума дают следующую систему уравнений (λ – множитель Лагранжа):
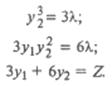
После подстановки первого уравнения во второе получим 3y1y22. Выразив из третьего уравнения 3у1, и подставив в последнее равенство, будем иметь (Z – 6y2)y22 = 2y23, откуда можно получить, что y2 = 1/8Z. Подставив этот результат в третье уравнение, получим у1 = 1/12Z. Таким образом, для данного примера функций спроса на товары у1 и у2 от дохода Z имеют вид:
Y1 = 1/12Z; у2 = 1/8Z
Однофакторные функции спроса от дохода широко применяются при анализе покупательского спроса. Соответствующие этим функциям кривые у1 = f1 (Z) называются кривыми Энгеля (по имени изучавшего их немецкого экономиста). Формы этих кривых для различных товаров могут быть различны. Если спрос на данный товар возрастает примерно пропорционально доходу, то функция будет линейной, как в рассмотренном выше примере. Такой характер имеет спрос на одежду, фрукты и т.д. Кривая Энгеля для этого случая представлена на рис. 25.6 А.
Если по мере роста доходов спрос на данную группу товаров возрастает все более высокими темпами, то кривая Энгеля выпукла (рис. 25.6 Б). Так изменяется спрос на предметы роскоши.
Если рост значений спроса по мере его насыщения отстает от роста дохода, начиная с определенного момента, то кривая Энгеля имеет вид вогнутой кривой (рис. 25.6 В). Например, таков характер спроса на товары первой необходимости.
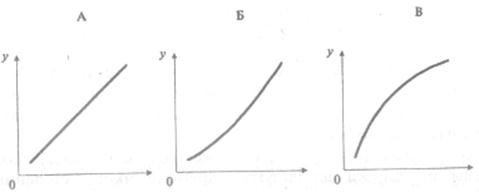
Рис. 25.6. Изменение спроса на товар по мере роста доходов
Тот же принцип разграничения групп товаров по типам функций спроса от дохода использовал шведский экономист Л. Торнквист, который предложил специальные виды функций спроса (функции Торнквиста) для трех групп товаров: первой необходимости, второй необходимости, предметов роскоши (рис. 25.7).
Функция Торнквиста для товаров первой необходимости имеет вид:
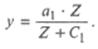
Она отражает тот факт, что рост спроса на эти первоочередные товары с ростом дохода постепенно замедляется и имеет предел а1 (кривая спроса асимптотически приближается к прямой линии у = a1); график функции на рис. 25.7 является вогнутой кривой (I).
Функция спроса по Торнквисту на товары второй необходимости выражается формулой:
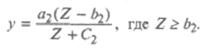
Функция также имеет предел а2 но более высокого уровня, при этом спрос на данную группу товаров появляется лишь после того, как доход достигнет величины b2, график функции на рис. 25.7 – вогнутая кривая (II).
Наконец, функция Торнквиста для предметов роскоши имеет вид:
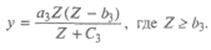
Функция не имеет предела. Спрос на эти товары возникает только после того, как доход превысит величину b3, и далее быстро возрастает, так что график функции на рис. 25.7 является выпуклой кривой (III).
Кроме указанных функций в аналитических моделях покупательского спроса используются другие функции: степенные, S-образные и т.д.
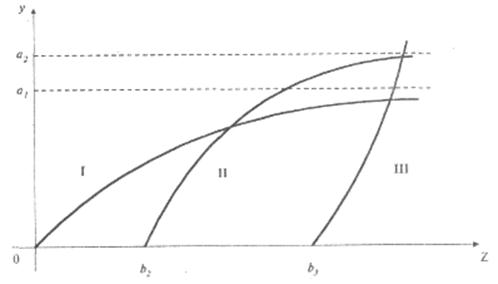
Рис. 25.7. Графики функций Торнквиста
Важную роль в анализе изменения спроса при небольших изменениях дохода играют коэффициенты эластичности. Коэффициент эластичности спроса от дохода показывает относительное изменение спроса при изменении дохода (при прочих неизменяющихся факторах). Он вычисляется по формуле:

где Еiz – коэффициент эластичности для i-го товара (группы товаров) по доходу Z;
yi – спрос на этот товар, являюющийся функцией дохода;
уi = fi (Z). Например, если спрос на товар описывается функцией Торнквиста для товаров первой необходимости, то формула (25.65) дает следующее выражение для коэффициента эластичности спроса от дохода:
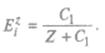
Во многих экономико-математических моделях эластичность функций относят к проценту прироста независимой переменной. Таким образом, коэффициент эластичности спроса от дохода показывает, на сколько процентов изменится спрос на товар при изменении дохода на 1%.
Коэффициенты эластичности спроса от дохода различны для разных товаров, они могут быть и отрицательны, когда с ростом доходов потребление уменьшается. Принято выделять четыре группы товаров в зависимости от коэффициента эластичности спроса на них от дохода: малоценные товары (ЕiZ < 0); товары с малой эластичностью (0 < ЕiZ < 1); товары со средней эластичностью (ЕiZ близки к единице); товары с высокой эластичностью (ЕiZ > 1).
К малоценным товарам, т.е. товарам с отрицательной эластичностью спроса от дохода, относятся такие, как хлеб, низкосортные товары. Судя по результатам обследований, коэффициенты эластичности для основных продуктов питания находятся в интервале от 0,4 до 0,8, для одежды, тканей, обуви – в интервале от 1,1 до 1,3 и т.д. По мере увеличения дохода спрос перемещается с товаров первой и второй групп на товары третьей и четвертой групп, при этом потребление товаров первой группы по абсолютным размерам сокращается.
Перейдем к анализу функций покупательского спроса от цен на товары. Из модели поведения потребителей (25.63) следует, что спрос на каждый товар в общем случае зависит от цен на все товары (вектора Р), однако построить функцию общего вида, выраженную как yi = φi(Р), очень сложно. Поэтому в практических исследованиях ограничиваются построением и анализом функций спроса для отдельных товаров в зависимости от изменения цен на этот же товар или группу взаимозаменяемых товаров: уi = φi (Р).
Для большинства товаров действует зависимость: чем выше цена, тем ниже спрос, и наоборот. Здесь также возможны различные типы зависимости и, следовательно, разные формы кривых. В практических задачах маркетинга важно различать действительное увеличение спроса, когда сама кривая сдвигается вверх и вправо (происходит переход с кривой I на кривую II на рис. 25.6), и увеличение объема приобретаемых товаров в результате снижения цен при неизменной сумме затрат (переход от точки А к точке Б по одной и той же кривой I на рис. 25.8).
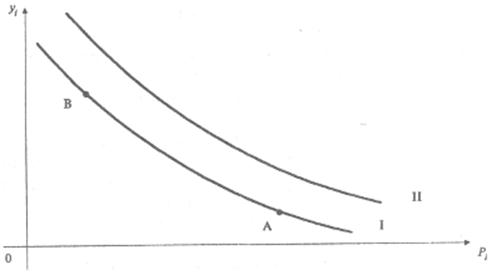
Рис. 25.8. Зависимость спроса на товары от уровня цен
Как уже отмечалось, в общем случае спрос на отдельный товар при прочих равных условиях зависит от уровня цен всех товаров. Относительное изменение объема спроса при изменении цены данного товара или цен других, связанных с ним товаров, характеризует коэффициент эластичности спроса от цен, который удобно трактовать как величину изменения спроса в процентах при изменении цены на 1%.
Для спроса yi, на i-й товар относительно его собственной цены р коэффициент эластичности исчисляется по формуле:

Значения коэффициентов эластичности спроса от цен практически всегда отрицательны. Однако по абсолютным значениям этих коэффициентов товары могут существенно отличаться друг от друга. Их можно разделить на три группы:
товары с неэластичным спросом в отношении цены (Еpii больше – 1);
товары со средней эластичностью спроса от цены (Еpii близко к – 1);
товары с высокой эластичностью спроса (Epii меньше – 1).
В товарах эластичного спроса повышение цены на 1% приводит к снижению спроса более чем на 1%, и наоборот, такое же понижение цены приводит к росту покупок больше чем на 1%. Если повышение цены на 1% влечет за собой такое же понижение спроса менее чем на 1%, то говорят, что это товар неэластичного спроса.
Рассмотрим, как влияет на спрос на какой-либо товар изменение цен на другие товары. Коэффициент, показывающий, на сколько процентов изменится спрос на данный товар при изменении на 1% цены на другой товар при условии, что другие цены и доходы покупателей остаются прежними, называется перекрестным коэффициентом эластичности. Для спроса уi на i-й товар относительно цены pj на j-й товар (i ≠ j) перекрестный коэффициент эластичности рассчитывается по формуле:
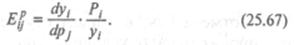
По знаку перекрестных коэффициентов эластичности товары можно разделить на взаимозаменяемые и взаимодополняемые. Если Epij > 0, это означает, что i-й товар заменяет в потреблении товар j, т.е. на товар i спрос переключается при увеличении цены на товар j. Примером взаимозаменяемых товаров могут служить многие продукты питания.
Если Epij < 0, это служит признаком того что i-и товар в процессе потребления дополняет товар j, т.е. увеличение цены на товар j приводит к уменьшению спроса на товар i. В качестве примера можно привести такие вазаимодополняемые товары, как автомобили и бензин.
В качестве иллюстрации в табл. 25.6 приведены значения прямых и перекрестных коэффициентов эластичности потребления от цен для некоторой категории семей. На основании этих данных по значениям прямых коэффициентов эластичности (по диагонали таблицы) можно сделать вывод: продукты питания в целом являются малоэластичными по отношению к цене; одежда, ткани и обувь имеют среднюю эластичность; две последние группы товаров являются товарами с высокой эластичностью спроса по отношению к цене.
Таблица 25.6
Прямые и перекрестные коэффициенты эластичности
|
Группы товаров |
Продукты питания |
Одежда, ткани, обувь |
Мебель, хозтовары |
Культтовары |
|
Продукты питания Одежда, ткани, обувь Мебель, хозтовары Культтовары |
-0,7296
-0,1991
-0,2458
-0,2494 |
0,0012
-1,000
0,0024
0,0024 |
0,0043
0,0071
-1,2368
0,0089 |
0,0045
0,0074
0,0092
-1,2542 |
На основании недиагональных элементов этой таблицы все промышленные товары (вторая, третья и четвертая группы) являются взаимозаменяемыми товарами. Положительность перекрестных коэффициентов эластичности по строке «Продукты питания» означает, что повышение цен на промышленные товары увеличивает спрос на продукты питания (уменьшение спроса на промышленные товары освободит средства для продуктов питания). Отрицательность перекрестных коэффициентов эластичности по столбцу (графе) «Продукты питания» означает, что при росте цен на продукты питания спрос на промышленные товары сокращается, поскольку это повышение уменьшает количество денежных средств, которые потребители выделяют на приобретение других товаров.
Моделирование и прогнозирование покупательского спроса. Очевидно, что спрос во многом определяет стратегию и тактику организации производства и сбыта товаров и услуг, поэтому учет спроса и обоснованное прогнозирование его на краткосрочную и долгосрочную перспективу являются важнейшими задачами службы маркетинга в различных организациях и фирмах.
Состав и уровень спроса на тот или иной товар зависит от многих факторов – как экономических, так и естественных. К экономическим факторам относятся уровень производства (предложения) товаров и услуг (обозначим этот фактор в общем виде П), уровень денежных доходов отдельных групп населения (D), уровень и соотношение цен (Р). К естественным факторам относятся демографический состав населения, в первую очередь размер и состав семьи (S), а также привычки и традиции, уровень культуры, природно-климатические условия и т.д.
Экономические факторы очень мобильны, особенно распределение населения по уровню денежных доходов, естественные же меняются сравнительно медленно и в течение небольшого периода (от года до пяти лет) не оказывают заметного влияния на спрос. Исключение составляет демографический состав населения. Поэтому в текущих и перспективных прогнозах спроса все естественные факторы, кроме демографических, целесообразно учитывать обобщенно, введя фактор времени (t).
Таким образом, в общем виде спрос определяется в виде функции перечисленных выше факторов:
y = f(П,D,P,S, t). (25.68)
Поскольку наибольшее влияние на спрос оказывает фактор дохода (есть даже выражение: «Спрос всегда платежеспособен»), многие расчеты спроса и потребления осуществляются в виде функции от душевого денежного дохода: у = f(D).
Наиболее простой подход к прогнозированию спроса на небольшой период времени связан с использованием так называемых структурных моделей спроса. При построении этих моделей исходят из того, что для каждой экономической группы населения по статистическим бюджетным данным может быть рассчитана присущая ей экономическая структура потребления. Однако предполагается, что на изучаемом отрезке времени заметные изменения претерпевает лишь доход, а цены, размер семьи и прочие факторы принимаются неизменными.
Изменение дохода, например его рост, можно рассматривать как перемещение определенного количества семей из низших доходных групп в высшие. Другими словами, изменяются частоты в различных интервалах дохода: они уменьшаются в нижних и увеличиваются в верхних интервалах. При этом семьи, которые попадают в новый интервал, будут иметь ту же структуру потребления и спроса, какая сложилась у семей с таким же доходом к настоящему времени.
Таким образом, структурные модели рассматривают спрос как функцию только распределения потребителей по уровню дохода. Имея данные о соответствующих структурах спроса, рассчитанных по данным статистики бюджетов, и о частотах распределения потребителей по уровню дохода, можно рассчитать общую структуру спроса. Если обозначить структуру спроса в группе семей со средним доходом Di через ω(Di), а частоты семей с доходом Di через r (Di), то общая структура спроса R может быть рассчитана по формуле:
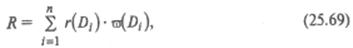
где п – количество интервалов доходов семей.
Структурные модели спроса являются одним из основных видов экономико-математических моделей планирования и прогнозирования спроса и потребления. В частности, широко распространены так называемые компаративные (т.е. сравнительные) структурные модели, в которых сопоставляются структуры спроса исследуемого объекта и некоторого аналогового объекта. Аналогом обычно считается регион или группа населения с оптимальными потребительскими характеристиками.
Наряду со структурными моделями в планировании и прогнозировании спроса используются конструктивные модели спроса. В основе их лежат уравнения бюджета населения, т.е. такие уравнения, которые выражают очевидное равенство общего денежного расхода (другими словами, объема потребления) и суммы произведений количества каждого потребленного товара на его цену. Если Z – объем потребления, т – количество разных видов благ, qi – размер потребления i-го блага, pi – цена i-го блага, то конструктивная модель спроса может быть записана следующим образом:

Вышеописанные модели, называемые также моделями бюджетов потребителей, играют важную роль в планировании потребления. К ним относятся всем известный прожиточный минимум, рациональные бюджеты, основанные на научных нормах потребления, прежде всего продуктов питания, перспективные бюджеты (например, так называемый бюджет достатка) и другие.
В практике планирования и прогнозирования спроса достаточно часто применяются аналитические модели спроса и потребления, которые строятся в виде уравнений, характеризующих зависимость потребления товаров и услуг от тех или иных факторов. Другими словами, в аналитических моделях функциональная зависимость (25.68) принимает вполне определенный вид. Такие модели могут быть однофакторными и многофакторными. Рассмотрим аналитические модели спроса на примере линейных корреляционно-регрессионных статических моделей, используя конкретные данные обследования семей.
В табл. 25.7 представлены статистические данные о расходах на питание, душевом доходе и размере семьи для девяти групп семей.
Таблица 25.7
Статистические данные о расходах на семью
|
№ группы |
Расход на питание (у) |
Душевой доход (x1) |
Размер семей (х2) |
|
1 |
433 |
628 |
1,5 |
|
2 |
616 |
1577 |
2,1 |
|
3 |
900 |
2659 |
2,7 |
|
4 |
1113 |
3701 |
3,2 |
|
5 |
1305 |
4796 |
3,4 |
|
6 |
1488 |
5926 |
3,6 |
|
7 |
1645 |
7281 |
3,7 |
|
8 |
1914 |
9350 |
4,0 |
|
9 |
2411 |
18807 |
3,7 |
Рассмотрим сначала однофакторную линейную модель зависимости расходов на питание (у) от величины душевого дохода семей (х1). Она выражается линейной функцией следующего вида:

Параметры a0 и а1 можно найти, решив систему нормальных уравнений, которая, в свою очередь, формируется с применением метода наименьших квадратов. Система нормальных уравнений для рассматриваемого случая имеет вид:
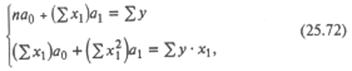
где суммирование проводится по всем n группам. Используя данные табл. 25.7, получим систему уравнений:
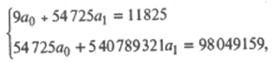
решением которой являются значения a0 = 549,68 и а1 = 0,1257.
Таким образом, модель имеет вид;

Уравнение (25.73) называется уравнением регрессии, коэффициент а1 называется коэффициентом регрессии. Направление связи между у и х1 определяет знак коэффициента регрессии а1 (в нашем случае данная связь является прямой). Теснота этой связи определяется коэффициентом корреляции:

где Sy есть средняя квадратическая ошибка выборки у в табл. 25.7. Она находится по формуле:
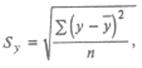
где 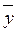 – средняя арифметическая значений у, а – средняя арифметическая значений у, а 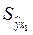 – средняя квадратическая ошибка нашего уравнения (25.73). Последняя определяется следующим образом: – средняя квадратическая ошибка нашего уравнения (25.73). Последняя определяется следующим образом:
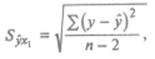
где 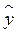 есть соответствующее значение, вычисленное по модели (25.73). В этих формулах, как и ранее, суммирование ведется по всем группам. есть соответствующее значение, вычисленное по модели (25.73). В этих формулах, как и ранее, суммирование ведется по всем группам.
Чем ближе значение коэффициента корреляции к единице, тем теснее корреляционная связь. В нашем примере Sy2 = 454 070, 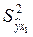 = 63 846, следовательно: = 63 846, следовательно:

Полученное значение 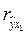 свидетельствует, что связь между расходами на питание и душевым доходом очень тесная. Величина свидетельствует, что связь между расходами на питание и душевым доходом очень тесная. Величина 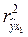 называется коэффициентам детерминации и показывают долю изменения (вариации) результативного признака под действием факторного признака. В нашем случае называется коэффициентам детерминации и показывают долю изменения (вариации) результативного признака под действием факторного признака. В нашем случае 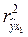 = 0,859; это означает, что фактором душевого дохода можно объяснить почти 86% изменения расходов на питание. = 0,859; это означает, что фактором душевого дохода можно объяснить почти 86% изменения расходов на питание.
Рассмотрим теперь двухфакторную линейную модель зависимости расходов на питание (у) от величины душевого дохода семей (х1) и размера семей (х2). Множественный (многофакторный) корреляционно-регрессивный анализ решает три задачи: определяет форму связи результативного признака с факторными, выявляет тесноту этой связи и устанавливает влияние отдельных факторов. В нашем случае эта модель имеет вид:

Параметры модели a0, а1 и а2 находятся путем решения системы нормальных уравнений:
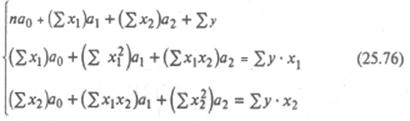
Используя данные табл. 25.7, получим систему нормальных уравнений в таком виде:
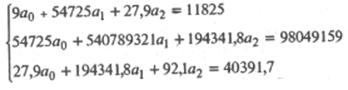
Решая эту систему (например, методом Гаусса), получим: a0 = 18,63; а1 = 0,0985; a2 = 224,6, так что модель (25.75) имеет вид:
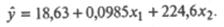
Для определения тесноты связи предварительно вычисляются парные коэффициенты корреляции 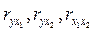 . Например: . Например:

где черта над символами означает среднюю арифметическую, a Sy и Sx1 – средние квадратические ошибки соответствующих выборок из табл. 27.7. Их можно вычислить следующим образом:
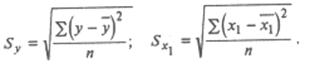
Аналогичный вид имеют формулы для 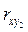 и и 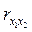 . .
После этого вычисляется коэффициент множественной корреляции:
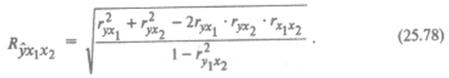
Данный коэффициент колеблется в пределах от 0 до 1; чем ближе он к единице, тем в большей степени учтены факторы, влияющие на результативный признак.
В нашем примере расчеты дают следующие значения коэффициента множественной корреляции: 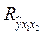 = 0,983, что выше значения коэффициента корреляции в случае однофакторной модели. Таким образом, связь расходов на питание с факторами душевого дохода и размера семей является очень высокой. = 0,983, что выше значения коэффициента корреляции в случае однофакторной модели. Таким образом, связь расходов на питание с факторами душевого дохода и размера семей является очень высокой.
Величина 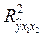 называется совокупным коэффициентом детерминации и показывает долю вариации результативного признака под воздействием изучаемых факторных признаков. В нашем примере называется совокупным коэффициентом детерминации и показывает долю вариации результативного признака под воздействием изучаемых факторных признаков. В нашем примере 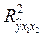 = 0,966; это означает, что совместное влияние = 0,966; это означает, что совместное влияние 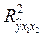 = 0,966; это означает, что совместное влияние душевого дохода и размера семей объясняет почти 97% изменения расходов на питание. = 0,966; это означает, что совместное влияние душевого дохода и размера семей объясняет почти 97% изменения расходов на питание.
Задача анализа тесноты связи между результативным и одним из факторных признаков при неизменных значениях других факторов решается в многофакторных моделях при помощи частных коэффициентов корреляции. Так, частный коэффициент корреляции между результативным признаком у и факторным признаком х1 при неизменном значении факторного признака х1 рассчитывается по формуле:
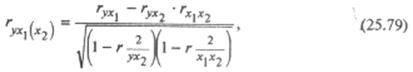
где используются парные коэффициенты корреляции, рассчитываемые по формулам, аналогичным (25.77). Аналогичная формула имеет место для частного коэффициента корреляции 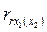 между результативным признаком у и факторным признаком x2 при неизменном значении факторного признака х1. между результативным признаком у и факторным признаком x2 при неизменном значении факторного признака х1.
Для рассматриваемого примера частные коэффициенты корреляции расходов на питание от душевого дохода и размера семей составляют:
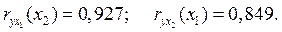
Это означает, что теснота связи между расходами на питание и одним из исследуемых факторов при неизменном значении другого весьма велика.
Если частные коэффициенты корреляции возвести в квадрат, то получим частные коэффициенты детерминации, показывающие долю вариации результативного признака под действием одного из факторов при неизменном значении другого фактора. В нашей задаче 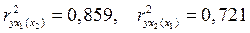 , следовательно, влиянием душевого дохода при неизменном размере семьи объясняется почти 86% изменения расходов на питание, а изменение размера семьи при неизменном душевом доходе объясняет более 72% изменения расходов на питание. , следовательно, влиянием душевого дохода при неизменном размере семьи объясняется почти 86% изменения расходов на питание, а изменение размера семьи при неизменном душевом доходе объясняет более 72% изменения расходов на питание.
Влияние отдельных факторов в многофакторных моделях может быть охарактеризовано с помощью частных коэффициентов эластичности, которые в случае линейной двухфакторной модели (25.75) считываются по формулам:
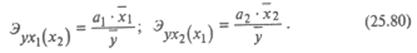
Черта над символом, как и ранее, означает среднюю арифметическую величину. Частные коэффициенты эластичности показывают, на сколько процентов изменится результативный признак, если значение одного из факторных признаков изменится на 1%, а значение другого факторного признака останется неизменным.
В рассматриваемом примере а1 = 0,0985; а2 = 224,6; 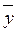 = 1313,9; = 1313,9; 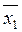 = 6080,6; = 6080,6; 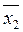 = 3,1, следовательно, по формулам (25.80) получим: = 3,1, следовательно, по формулам (25.80) получим:
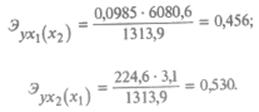
Это означает, что при увеличении душевого дохода на 1% и неизменном размере семьи расходы на питание увеличатся на 0,456%, а увеличение (условное) на 1% размера семьи при неизменяем душевом доходе приведет к возрастанию расходов на питание на 0,530 %.
Вопросы для повторения
1. Перечислите важнейшие методы экономико-математического моделирования и сферы их оптимального применения в маркетинге.
2. Каков характер применения балансовых моделей в маркетинге?
3. Раскройте сущность модели межотраслевого баланса.
4. Опишите назначение и структуру оптимизационных моделей. Какие задачи маркетинга можно решать с их помощью?
5. Какие важнейшие методы и модели управления товарными запасами используются в маркетинге?
6. Перечислите основные системы регулирования товарных запасов и дайте их краткие характеристики.
7. Дайте определение понятия целевой функции потребления и кривых безразличия.
8. В чем суть построения функций спроса от дохода?
9. Назовите особенности построения структурных и конструктивных моделей спроса.
10. Опишите построение аналитических моделей спроса и потребления на основе корреляционно-регрессивного анализа. | 