| Главная » Учебно-методические материалы » СТАТИСТИКА » Общая теория статистики: учебник. Под ред. Елисеевой И.И. |
| 23.01.2012, 19:33 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Само слово индекс (index) означает показатель. Обычно этот термин используется для некоей обобщающей характеристики изменений. Например, уже знакомый вам индекс Доу Джонса, индекс деловой активности, индекс объема промышленного производства и т. д. Гораздо реже термин «индекс» используется как обобщенный показатель состояния, например, известный индекс интеллектуального развития IQ. В этой главе мы рассмотрим индексы прежде всего как показатели изменений. Очевидно, что сфера использования таких показателей безгранична: спортсмены стремятся улучшить свои достижения, предприниматель желает увеличить прибыль и т.д. Во всех этих случаях необходимо выразить изменения количественно. Как изменились цены, уровень жизни, покупательная сила денег и пр.? Ответы на все эти вопросы позволяют дать индексы. 10.1. Понятие индексаВ предыдущей главе вы познакомились с показателями, которые измеряют абсолютные и относительные изменения: темпы роста, прироста, абсолютный прирост, цепные и базисные показатели, показатели средних изменений за период. В чем же специфика индексов? Принципиальных отличий три. Во-первых индексы позволяют измерить изменение сложных явлений. Например, нужно определить, как изменились за год расходы жителей Москвы на городской транспорт. Для ответа на этот вопрос вы должны иметь численность пассажиров, перевезенных за год каждым видом городского транспорта, рассчитать среднемесячную численность пассажиров или взять точные данные из отчетов по месяцам, умножить численность на тариф перевозки (и число месяцев его действия - в случае использования среднемесячной численности) и полученные величины просуммировать. То же нужно сделать по данным за прошлый год. Затем сопоставить сумму расходов за последний год с суммой за прошлый год. То есть это не просто сравнение двух чисел, как при расчете темпов динамики или приростов, а получение и сравнение некоторых агрегированных величин. Во-вторых, индексы позволяют проанализировать изменение -выявить роль отдельных факторов. Например, можно определить, как изменилась сумма выручки городского транспорта за счет изменения численности пассажиров и тарифов, наконец, за счет соотношения в объеме перевозок разными видами транспорта. В-третьих, индексы являются показателями сравнений не только с прошлым периодом (сравнение во времени), но и с другой территорией (сравнение в пространстве), а также с нормативами. Например, интересно знать, не только как изменилось среднедушевое потребление мяса в России в данном году по сравнению с прошлым годом (или с каким-либо другим периодом), но и сравнить показатели среднедушевого потребления мяса в России и развитых странах Запада, Востока, а также провести сравнение с нормативной величиной, отвечающей нормам рационального питания. Очевидно, что каждое направление сравнения вносит что-то новое. Так, удой молока на одну корову в хозяйствах Российской Федерации в 1990 г. составил 2781 кг, а в 1989 - 2773 кг. Индекс равен 100,3% (+0,3) ≠ [2781 : 2773 = 1,0029·100%]. Повышение - 8 кг на одну корову, такое сравнение вроде внушает хотя и умеренный, но оптимизм. Если же сравнить с удоем в других странах, то те же данные выглядят так: в Великобритании в 1990 г. этот показатель был равен 5213 кг/корову, Польше - 3234, Швеции - 6213 кг/корову. Соответствующие индексы составили 53,3; 86; 44,8%. Существует несколько определений индекса. Приведем одно из них, может быть самое краткое. Индекс - это показатель сравнения двух состояний одного и того же явления (простого или сложного, состоящего из соизмеримых или несоизмеримых элементов). Каждый индекс включает два вида данных: оцениваемые данные, которые принято называть отчетными и обозначать значком «1», и данные, которые используются в качестве базы сравнения -базисные, обозначаемые знаком «О». Индекс, который строится как сравнение обобщенных величин, называется сводным или общим, и обозначается i. Если же сравниваются необобщенные величины, то индекс называется индивидуальным и обозначается i. Как правило, подстрочно дается значок, который указывает, для оценки какой величины построен индекс. Например, Iq1/10 или iq1/10 , т. е. сводный и индивидуальный индексы для величины q. . Сравнения во времени могут охватывать короткий период: выработка за этот день и за вчерашний день, цены в сентябре по сравнению с августом и т. д. Но сравнение может проводиться и с отдаленным периодом: современные данные с довоенным 1940 г. или с 1986 г. - годом начала перестройки, когда экономика еще не была затронута структурными изменениями и т. д. Выбор базисного периода всегда аргументирован той задачей, для которой строится индекс. Обычно руководствуются двумя правилами: либо база сравнения представляет стабильный уровень, либо экстремальное значение - высшее достижение или низший уровень (в случае падения экономических показателей). Конечно, сравнение с отдаленным периодом вносит дополнительные трудности, что уже отмечалось в предыдущей главе. Некоторые специфические для построения индексов проблемы будут затронуты ниже. 10.2. Индекс как показатель центральной тенденции (индекс средний из индивидуальных)Вы можете услышать, что уровень потребительских цен понизился или повысился. Речь в этом случае идет об индексе цен на потребительские товары. Общее изменение образуется под влиянием изменений цен на отдельные товары. Таким образом, мы имеем ряд отношений: Эти отношения есть не что иное, как индивидуальные индексы, и сводный индекс представляет собой средний из них: где j - номер товара. Так как средняя есть показатель центра распределения, то и сводный индекс можно назвать показателем центральной тенденции. Проблема состоит в том, как получить этот сводный индекс. Впервые она возникла при попытке оценить совокупное изменение цен либо в виде отношения сумм цен: либо как среднее из изменений цен на отдельные товары: В том и другом варианте представлены невзвешенные средние. Первый вариант исходит из того, что цена рассчитывается за единицу товара, например за 1кг, и сумма цен может рассматриваться как набор слагаемых с равными весами. Однако, этот вариант не отвечает задаче осреднения показателей изменений цен на отдельные товары. Второй 'вариант настораживает тем, что согласно общему правилу средняя из относительных величин должна вычисляться как средняя взвешенная. Действительно, если говорить конкретно об измерении динамики цен на все продовольственные или непродовольственные товары, то ясно, что если цены на ювелирные изделия из золота удвоятся, а цены на хлеб останутся неизменными, это не значит, что в целом цены выросли на 50% ((2+ 1)/2 = 1,5). Приведенный пример показывает, что индекс цен для каждого товара должен сопровождаться неким «весом», который позволяет оценить относительную значимость этого индекса для потребителя. В качестве веса используют удельный вес в общей стоимости покупок: в базисном периоде: Если обозначить удельный вес отдельных затрат с1ц„ то получим общий индекс цен как средний арифметический взвешенный из индивидуальных индексрв цен: т.е. Ip = i̅p.. Используя формулу (10.2) можно получить общее изменение цен на продукты по данным табл. 10.1. Часто можно встретить утверждение, что чем сильнее варьируют веса средней, тем значительнее отличие невзвешенной средней от взвешенной. Покажем ошибочность этого утверждения применительно к индексу среднему из индивидуальных. Рассмотрим два примера А и Б. А. Равенство взвешенной и простой средних при сильной вариации весов. В табл. 10.1 представлены данные примера А. Таблица 10.1
Невзвешенный средний индекс цен Среднее значение веса Взвешенный средний индекс цен Результат совпадает с простой средней. Между тем вариация весов значительна, стандартное отклонение Коэффициент вариации весов Б. Неравенство взвешенной и простой средних при слабой вариации весов. В табл. 10.2 представлены данные примера Б. Таблица 10.2
невзвешенный средний индекс цен: взвешенный средний индекс цен вариация весов vd = 0,2366 или 23,7%, т. е. вариация весов намного слабее, чем в примере А. Рассмотрим, в чем секрет таких соотношений? Обратимся к формуле взвешенной средней: где x̅, f̅ - простые средние; Dх, Df - отклонения от них. Представим последнее выражение как: Числитель второго слагаемого можно представить через коэффициент корреляции между х и f: Эта формула аналогична формуле (5.6). Следовательно, средняя взвешенная равна простой средней, если: • вариация признака х, отсутствует, т. е. sx = 0; • вариация -весов fi отсутствует, т. е. vf = 0; • нет корреляции между вариациями признака и весов, т. е. rxf = 0 (хотя бы сами х, и f, варьировали как угодно сильно). Отношение взвешенной средней и простой можно выразить следующим образом: Поскольку различие взвешенной и простой средних зависит от корреляции значений признака и веса, постольку оно может оказаться большим при слабой вариации весов, чем при их сильной вариации (см. главу 5). Рассмотрим соотношения между индексами (10.1) и (10.2) на примере табл. 10.3. Таблица 10.3 Данные розничной торговли города N
Обратите внимание на данные гр. 5 табл. 10.3: произведение q0p0ip имеет не просто техническое значение взвешивания индивидуального индекса, но дает определенный содержательный результат -показатель условных затрат на покупку с учетом изменения цен q0 · p0 · ip = q0 · p1 Это дает право представить формулу (10.2) в виде: Выражение (10.5) получило известность как индекс Ласпейреса, предложившего эту формулу в 1864 г. По данным табл. 10.3 т. е. цены возросли в среднем на 7,1%. Если воспользоваться формулой (10.1), то Ip = 641,2/6 = 1,069 • 100 = 106,9%, т. е. в среднем цены возросли на 6,9%. Отличие от среднего взвешенного арифметического индекса составляет 0,2%. Мы рассмотрели определение среднего изменения на основе средней арифметической из индивидуальных, но ведь могут использоваться и другие виды средних: средняя геометрическая, средняя гармоническая и т. д. - невзвешенные и взвешенные. Используя среднюю геометрическую невзвешенную, получаем:
Средняя гармоническая всегда дает результат, меньший средней арифметической. Применяя среднюю гармоническую невзвешенную, получаем:
Опять-таки деление единицы на каждый индекс предполагает равное значение изменения цен на товары, что не соответствует практике. Используя в качестве весов затраты на покупку в отчетном периоде, получаем сводный индекс цен как средний гармонический взвешенный из индивидуальных индексов цен: В формуле (10.6) и далее для простоты мы опустили подстрочный значок, соответствующий номеру товара (элемента), хотя, конечно же, суммирование и в числителе, и в знаменателе производится по всему набору товаров (элементов). Рассчитаем этот индекс по данным табл. 10.3. Кроме того, нам потребуются дополнительные данные. Как всегда, лучшей формой представления цифровых данных является таблица. Представим все необходимые данные в табл. 10.4, используя вместо названий номера продуктов. Таблица 10.4 Данные розничной торговли города
Результат совпал с тем значением / , которое было получено по формуле (10.2). Но это случайное совпадение, которое оказалось возможным из-за слабой корреляции между изменением уровня цен и объема продаж отдельных товаров. Это может быть при сравнении за короткий период. В рыночной экономике взаимосвязь между колебаниями цен и объема продаж проявляется при сравнении за более длительный период. Ниже будет показано, как измерить величину этой корреляции (см. формулу (10.17). Знаменатель формулы (10.6) имеет смысл затрат на покупку «отчетного» количества товаров по базисным ценам: Тогда формула (10.6) может быть представлена как Эта формула индекса цен была предложена Пааше в 1874 г. Различие между индексами Пааше и Ласпейреса, их использование обсуждаются ниже в данной главе. Итак, мы рассмотрели применение разных форм и видов средних величин для определения среднего изменения цен по всем товарам. Люди всегда в первую очередь интересовались ценами и их изменениями. Но такой же подход может быть применен к оценке сводных изменений других характеристик, например объема (количества) покупок товаров. Кстати заметим, что используемые нами обозначения цен (р), количества (q) неслучайны и соответствуют начальным буквам английских слов price (цена) и quantity (количество). Это закрепленные обозначения в статистике. Таким образом, общее изменение количества проданных товаров формируется как среднее по отношению к изменениям объема покупок отдельных товаров, т. е. Возникает вопрос о порядке расчета средней из iq: средняя арифметическая - простая или взвешенная - или другая форма средней. Ограничимся рассмотрением только средней арифметической. По данным табл. 10.4 простая средняя арифметическая из индивидуальных индексов количества равна:
Используя в качестве весов для изменений объема покупок удельный вес покупок в общей сумме затрат, получаем: т. е. индекс Iq - средний арифметический взвешенный из индивидуальных iq. По данным нашего примера (табл. 10.3 и 10.4) общий индекс количества равен: Получилось, что объем покупок продовольственных товаров сократился в среднем на 1,5%. Это более значительная оценка снижения, нежели полученная при расчетах по простой средней арифметической (- 0,6%). Так что мы еще раз получили подтверждение зависимости результата от использованной формулы. Зная среднюю величину изменения показателя и индивидуальные индексы, можно проводить анализ методами вариационной статистики: анализировать распределение товаров по изменению цен, объема покупок, сравнивать модальное и среднее изменение, максимальное и минимальное; по показателям эксцесса распределений делать выводы о том, насколько однородны изменения цен и количества по отдельным товарам, группировать товары по уровню цен и степени их изменения и т. д. 10.3. Агрегатные индексы. Система индексовМы познакомились с построением сводных индексов на основе индивидуальных. Однако возможен и другой путь. Обратимся к формулам индексов Ласпейреса (10.5) и Пааше (10.7). Эти индексы могут быть рассчитаны на основе данных о количестве проданных товаров в базисном и отчетном периоде (по каждому j-му товару) q0j и q1j и ценах – р1j и р0j. Такие индексы принято называть агрегатными. Так же можно построить и Iq не через осреднение индивидуальных индексов, а на основе сравнения двух сумм (агрегатов), см. (10.7). Агрегатные индексы считаются основной формой индексов. Они выполняют две функции: синтетическую и аналитическую. Первая функция обеспечивается тем, что в одном индексе обобщаются (синтезируются) непосредственно несоизмеримые явления. Например, цены на разные товары или разные товары, абсолютно не сопоставимые между собой в натуральном выражении. Когда мы записываем то благодаря использованию ценового соизмерителя можно агрегировать данные по различным товарам. Вторая функция - аналитическая - следует из взаимосвязи индексов. Дело в том, что практически каждый индекс можно рассматривать как составляющую некоей системы индексов, в которой его роль сводится к измерению одного из факторов общего изменения сложного явления и вклада этого фактора в совокупное изменение. Так, например, индекс цен можно рассматривать как показатель влияния изменения цен на выручку от продажи. Такая трактовка опирается на следующую связь признаков: количество цена = выручка (или затраты на покупку), т. е. qp = w. (10.9) Системе признаков соответствует система индексов (т. е. показателей их изменений). Исходя из этого можно записать: Обратите внимание: эта запись соответствует трактовке индекса как метода анализа. Когда мы указываем Iw(q) или Iw(p) то имеем в виду измерение общего изменения результативного явления (в данном случае w) за счет одного из факторов (q или р). Конечно, можно ограничиться записью Iq и ip - ничего не изменится по существу. При построении агрегатных индексов удобно пользоваться такими понятиями, как «индексируемый признак» и «признак-вес». Индексируемый - это признак, изменение которого характеризует данный индекс. Например, в Iq - это q, в ip – это p. Значение индексируемого признака изменяется: отчетное значение сопоставляется с базисным. Признак-вес выполняет функцию веса по отношению к индексируемому признаку; его значение в данном индексе принимается неизменным, так как он не должен искажать оценку изменения индексируемого признака. В Iq признаком-весом является р, а в Ip - q. Индексируемый признак можно назвать фактором изменения общего результата, а признак-вес - характеристикой условий, в которых оценивается это изменение. Если индексы рассматриваются в системе, то должна обеспечиваться взаимосвязь между ними. Например, в соответствии с (10.9) должно выполняться равенство
Обратимся к формулам (10.11). Каждый из индексов показывает, как изменился тот или иной фактор при неизменности прочих условий: и в формуле индекса Iq и в формуле Ip веса закреплены на базисном уровне. Это обеспечивает сопоставимость оценок изменений факторов. Однако равенство (10.11) не обеспечивается или, как говорят иначе, не обеспечивается увязка индексов в систему: То же происходит, если все индексы будут построены с отчетными весами: Только когда взаимосвязанные индексы строятся с весами разных периодов, увязка их в систему выполняется: или Из этих двух вариантов отечественная статистика долгое время отдавала предпочтение второму. Соответственно существовало правило определения периода весов: индексы первичных признаков строятся на весах базисного периода, вторичных - на весах отчетного периода. Это правило признавало неравное значение признаков в системе: первичный признак выступает как основа формирования нового (отчетного) значения результативного признака w1. Этим объясняется то, что индекс первичного признака (например, Ip) оценивает изменение этого признака при сохранении базисных условий, тогда как изменение вторичного признака оценивается уже в изменившихся условиях, когда первичный признак принял значение отчетного периода. Рассмотрим на примере, как влияет использование разных значений признака-веса на величину индекса (табл. 10.5). Таблица 10.5 Данные о продаже продуктов на городском рынке за месяц
В обоих вариантах получены показатели снижения объема продажи и роста цен, но в первом случае объем продажи снизился на 3,58%, цены повысились на 3,7%, а во втором - снижение объема продажи на 3,7% и рост цен на 3,78%. Следуя статистической логике, можно сказать, что точечные оценки в принципе невозможны; можно говорить лишь о поле или интервале оценок: для объема продажи - снижение от -3,58% до - 3,7%; для цен - рост от 3,7% до 3,78%. Однако в практическом использовании индексов стремятся получить однозначное решение тем или иным способом. Первый путь - получение средних оценок изменений: либо в форме индексов, построенных на средних весах: либо через осреднение разновзвешенных индексов. При этом предпочтение отдается средней геометрической: Второй путь основан на предпочтении какого-то одного варианта построения взаимосвязанных индексов. Как уже отмечалось, в отечественной статистике был принят второй вариант. Но при этом возникала несопоставимость оценок изменений признаков. Поэтому делалась попытка построения всех взаимосвязанных индексов на весах одного периода - базисного: Понятно, что в этом случае не выполняется увязка индексов в систему:
Изолированная оценка изменения каждого фактора при неизменности другого приводит к недоучету эффекта совместного изменения факторов. Скажем, вы смотрите движущееся изображение без звука или слушаете звуковое сопровождение без изображения, и в том, и в другом случае воздействие меньше, чем при соединении изображения и звука. Наглядно это можно показать с помощью особого вида плоскостной диаграммы, известной в отечественной статистике как «знак Варзара» (по имени русского статистика В. Е. Варзара (1851-1940) (см. рис. 10.1). Результативное явление представлено здесь в виде прямоугольника, площадь которого в базисном периоде
В статистической науке выработано множество версий такого разложения: 1) выделение эффекта взаимодействия факторов в самостоятельный член; 2) присоединение его к какому-либо одному фактору (т. е. построение какого-либо из индексов на весах отчетного периода); 3) разделение эффекта взаимодействия факторов и присоединение к изменениям факторов - поровну, либо пропорционально значениям индексов факторов, либо еще по какому-то принципу. Вы можете тоже попытаться предложить свое решение - актуальность проблемы сохраняется. В. И. Борткевич (1868-1931) вывел формулу, объясняющую различие между индексами с разными весами: Точно так же можно выразить соотношение между индексами фактора q с разными весами. Из формулы (10.17) ясно, что индексы с отчетными и базисными весами будут равны, если выполняется хотя бы одно из условий: или корреляция между изменениями цен и объема продажи на отдельные товары отсутствует, Ничего не меняется, если результативный признак включает более двух факторов, т. е. в случае мультипликативной модели: y = x1 ·x2…..xk Если придерживаться концепции неравноправия факторов и строить индексы с разными весами, то все зависит от принятой последовательности факторов в системе. Например, общие затраты на кожу для изготовления женских туфель можно представить как w = qlp, где q - количество пар туфель; l - средний расход кожи на одну пару; р - цена кожи. Первым стоит фактор q как первичный, с которого и начинаются все изменения. Тогда индексы будут иметь вид: Здесь используется то же правило выбора весов, которое было сформулировано выше. Признаки, стоящие слева от индексируемого признака, трактуются по отношению к нему как первичные и закрепляются на отчетном уровне (они «уже» изменились), стоящие справа от него трактуются как вторичные и закрепляются на базисном уровне (они как бы «еще» не изменились). К этому добавляется условие содержательной интерпретации при последовательном объединении признаков слева направо. Скажем, произведение ql имеет экономический смысл — это расход кожи на весь объем производства туфель, при перестановке признаков q, р, l произведение qp экономического смысла не имеет. На таком подходе основан метод цепных подстановок, широко используемый в экономическом анализе. \ Если же все индексы строятся на весах одного и того же (базисного) периода, то последовательность признаков не имеет значения. Система индексов будет иметь вид:
И в этом случае многофакторной модели эффект совместных изменений можно либо сохранить как самостоятельный член разложения, либо распределить между изменениями факторов. Это зависит от поставленной задачи и от пристрастий исследователя. Сравнение данных отчетного и базисного периодов неявно предполагает представление экономических процессов в виде дискретной последовательности периодов времени, что особенно проблематично при сравнении в длительном периоде. Экономические индексы для моментов непрерывного времени были предложены в 1928 г. французским статистиком Ф. Девизиа. Это привело к использованию в индексном анализе дифференциального исчисления. Данный подход до сих пор не вошёл в статистическую практику, однако теоретически он более обоснован, нежели традиционные методы. 10.4. Свойство индексовКак было показано, в построении индексов возникает много дискуссионных вопросов. Индексы считаются построенными правильно, если они удовлетворяют ряду тестов. Эти тесты были сформулированы американским статистиком И. Фишером (1867 - 1947). Основные тесты таковы: 1. Тест обратимости во времени. Индексы, исчисленные в «прямом» и «обратном» направлениях, должны быть взаимообратными числами. Например, если индекс показывает, что уровень цен в отчетном периоде по сравнению с базисным повысился в два раза, то он должен отражать, что в базисном периоде цены были вполовину ниже, чем в отчетном, т. е.
где а и b — сравниваемые периоды. Очевидно, что наличие этого свойства желательно у любого индекса, ибо в таком случае сравнение между двумя состояниями не будет зависеть от того, какое из них принято за базу, особенно это важно при территориальных сравнениях. 2. Тест обратимости по факторам. Если поменять местами в индексе цен символы для цен и для количества, то мы должны получить индекс количества, который, будучи умножен на индекс цен, должен дать изменение общей стоимости товаров. Например, имеем: Если теперь поменять местами р и q, то получим: Произведение этих индексов не равно индексу общей стоимости 3. Тест кружного испытания (циркулярность). Если построен некоторый индекс для года а при базисном годе b и для года b при базисном годе с, то из них можно получить индекс года а при базисном годе с. Тест кружного испытания требует, чтобы Ia/c, основанный на промежуточных сравнениях, совпал с тем, какой мы получили бы при непосредственном сравнении а с с, т. е. Ia/b · Ib/c = Ia/c Это требование принято называть, в статистике «цепным тестом». В случае взвешенных индексов этот тест выполняется только для индексов с постоянными весами. Особенно трудно обеспечить выполнение этого теста при сравнении с отдаленной базой. Легко сравнивать каждый из ряда лет с предыдущим, но нелегко сравнивать удаленные годы: произведение цепных сравнений (между прилежащими годами) может отличаться от результатов непосредственного сравнения лет в начале и конце периода. Тут возникает много экономических проблем — и постоянство весов (проблема выбора неизменных цен при построении индексов объема производства), и выделение сравнимого круга элементов на протяжении всего периода (сравнимого круга товаров, видов продукции труда и т. д.) при анализе изменений цен, заработной платы и т. п. В этот же тест Фишер вводил условие круговой сходимости, которое гласит: если условия начального и конечного моментов времени совпадают по уровням цен и объемов товаров, то произведение индексов цен и объемов товаров за все подпериоды должно быть равно единице. 4. Соизмеримость. Численные значения индексов не должны зависеть от выбора единиц измерения объема товаров и цен. 5. Пропорциональность. Согласно данному тесту, если темпы роста всех цен (или объемов товаров) равны одному и тому же числу, то этому же числу должен быть равен индекс цен (или индекс объема). 6. Включение - исключение. Если к набору товаров, по которым вычисляются индексы, и объему товаров, добавить еще один товар, темпы роста цены (или объема) которого совпадают с первоначальным индексом, то первоначальный индекс цен (или объема) не должен измениться. Как видим, формулировка всех тестов основана на логике построения экономико-статистических показателей. Тесты сыграли большую роль в развитии методологии экономических индексов. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

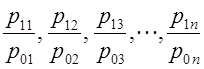 и т.д.
и т.д. ,
,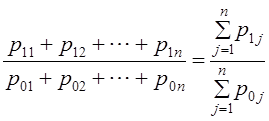 ,
,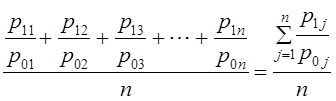 (10.1)
(10.1)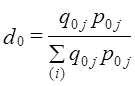
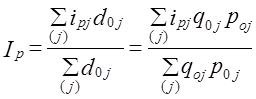 (10.2)
(10.2)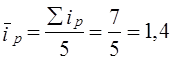
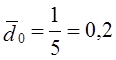

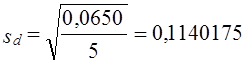
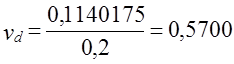 , т.е. 57%.
, т.е. 57%.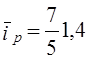
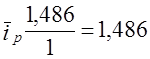 ;
;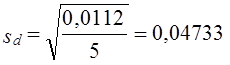


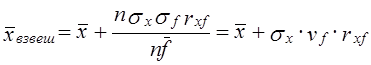 (10.3)
(10.3) (10.4)
(10.4)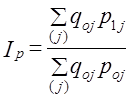 (10.5)
(10.5)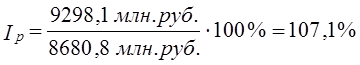
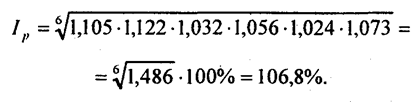
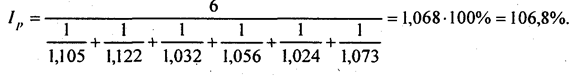
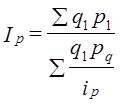 (10.6)
(10.6)
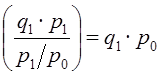
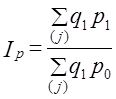 (10.7)
(10.7) , где
, где 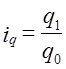
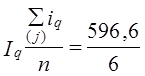 = 0,994·100% = 99,4%(- 0,6%).
= 0,994·100% = 99,4%(- 0,6%).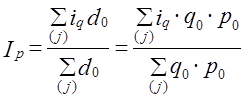 (10.8)
(10.8)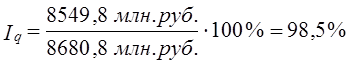
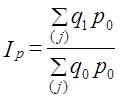 ,
,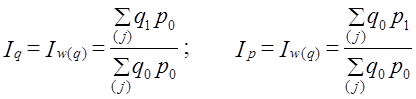 (10.10)
(10.10)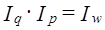 (10.11)
(10.11)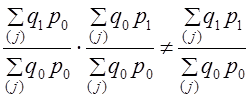
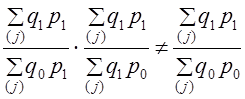
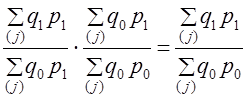 (10.12)
(10.12)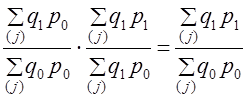 (10.13)
(10.13)

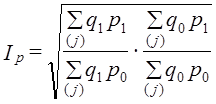 (10.14)
(10.14)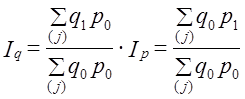 (10.15)
(10.15)
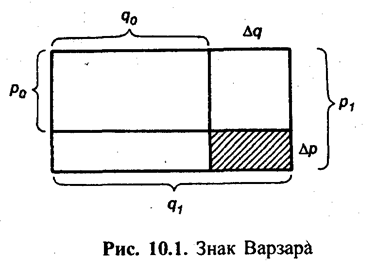
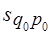 , в отчетном -
, в отчетном - 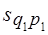 . Переход от базисного состояния к отчетному формируется за счет изменения фактора
. Переход от базисного состояния к отчетному формируется за счет изменения фактора 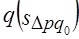 , изменения фактора
, изменения фактора 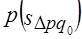 и совместного изменения обоих факторов
и совместного изменения обоих факторов 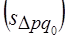 :
: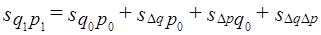 (10/16)
(10/16)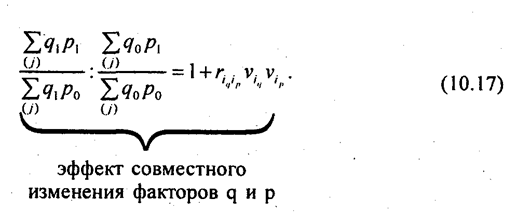
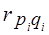 = 0; или темпы изменения объемов товаров всех видов будут oдинаковы,
= 0; или темпы изменения объемов товаров всех видов будут oдинаковы, 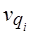 = 0; или темпы изменений цен на все товары будут одинаковы,
= 0; или темпы изменений цен на все товары будут одинаковы, 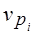 = 0. Чем большая дистанция разделяет сравнимые периоды, тем сильнее проявляются все отмеченные факторы различий между индексами с разными весами.
= 0. Чем большая дистанция разделяет сравнимые периоды, тем сильнее проявляются все отмеченные факторы различий между индексами с разными весами.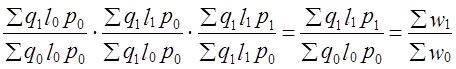 (10.18)
(10.18)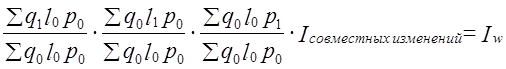 (10/19)
(10/19)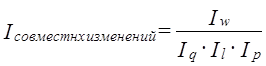
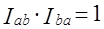 , (10.20)
, (10.20)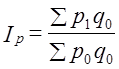
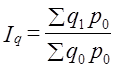
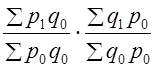
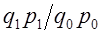 . Следовательно, индексы этого типа не отвечают тесту обратимости факторов. Тесту обратимости отвечает средний геометрический индекс (10.14). По этой причине он был назван И. Фишером идеальным индексом.
. Следовательно, индексы этого типа не отвечают тесту обратимости факторов. Тесту обратимости отвечает средний геометрический индекс (10.14). По этой причине он был назван И. Фишером идеальным индексом.