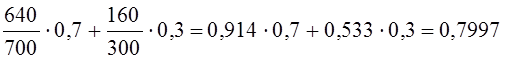| Главная » Учебно-методические материалы » СТАТИСТИКА » Общая теория статистики: учебник. Под ред. Елисеевой И.И. |
| 23.01.2012, 19:34 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
10.5 Индексный анализ взвешенной средней. Индекс структурыИндексы позволяют анализировать изменения не только агрегатов, но и средних величин. Предположим, изучается динамика средней цены товара на трех рынках города, расположенных в разных районах - центральном и двух периферийных - старой и новой застройки. Уровень цен в этих районах разный, соответственно на среднюю цену продажи на колхозных рынках влияют не только цены на каждом из них, но и доля каждого рынка в общем объеме продажи. Формула средней цены: где рi - цена товара на i-м рынке.
Изменение средней цены (как и любой взвешенной средней) выражается индексом: Этот индекс получил название индекса переменного состава, так как отражает не только изменение осредняемого признака р, но и структуры совокупности Этот индекс получил название индекса постоянного состава. Соответственно Формулы индексов (10.23) и (10.24) основаны на общепринятом правиле, по которому структура совокупности как первичная характеристика при индексации цен закрепляется на уровне отчетного периода, а цены как вторичная характеристика при индексации структуры закрепляются на уровне базисного периода. Очевидно, что применение весов разных периодов и в этом случае обеспечивает выполнение равенства: Конечно, можно все индексы построить на весах базисного периода, и это будет правильнее с точки зрения оценки изменения каждого из факторов, но тогда равенство (10.25) будет нарушено. Рассмотрим построение этих индексов на примере. На трех рынках города продается картофель. Данные о продаже за день в зарегистрированных ценах приведены в табл. 10.6. Таблица 10.6 Дневная продажа картофеля на колхозных оынках города
Средняя цена картофеля в августе составила р̅0 =1,65 тыс. руб./кг, в сентябре p̅1= 2,08 тыс. руб./кг. Наибольший рост цен произошел на рынке в новом районе, но здесь же и наибольшее увеличение объема продаж, в результате чего доля этого рынка в общей дневной реализации картофеля в сентябре стала превышать половину всего объема. Индекс средней цены составил: Iр = 2,08 тыс. руб:/кг : 1,65 тыс. руб./кг = 1,259·100% = 125,9% Изменение самой цены в условиях структуры продажи, сложившейся в отчетном периоде, составило:
т. е. среднее повышение цен на рынках было несколько меньшим, чем повышение средней цены (+23,5% против +25,9%). Эту величину мы получили делением средней цены в отчетном периоде на среднюю условную цену, которая была бы при базисном уровне цен на рынках и отчетной структуре продаж. Этот же индекс можно было получить как отношение сумм выручки в отчетном периоде к условной выручке: Различие между индексом постоянного состава Ip и индексом переменного состава Ip̅ вызвано изменением структуры: Iструктуры = 168,4 : 165,2 = 1,019·100% =101,9%. За счет изменения структуры продажи средняя цена картофеля на колхозных рынках повысилась на 1,9%. Это связано с повышением удельного веса нового рынка, на котором цены выше. Очевидно, что выполняется равенство 1,235·1,019 = 1,259. Если использовать обозначение структуры продажи d, то индексы (10.22), (10.23), (10.24) будут иметь вид: Можно выразить и абсолютное изменение средней величины с учетом изменения факторов-самого осредняемого признака и структуры (т. е. признака-веса):
По данным табл. 10.6 средняя цена картофеля повысилась на 43 руб./кг: Δp̅ = 2,08 - 1,65 = 0,43 руб./кг; в том числе за счет самой цены Δp̅(р) = 2,08 - 1,68 = 0,4 руб./кг и за счет структурного фактора Δp̅(d) = 1,68 - 1,65 = 0,03 руб./кг. И при относительном, и при абсолютном разложении эффект взаимодействия факторов - цены и структуры продажи - присоединился к оценке изменения цен. Если получить эту оценку в условиях базисного периода, то сравнение индексов
позволит выделить эффект совместного изменения факторов. По данным табл. 10.6 получаем: Этот результат мало отличается от того, который был получен в условиях структуры продажи отчетного периода (1р = 1,259), так что эффект взаимодействия факторов оказался незначителен и направлен на повышение средней цены. Влияние структурных сдвигов может привести к неожиданным результатам: изменение себестоимости в целом по отрасли может оказаться большим, чем на отдельных предприятиях; или при выполнении производственной программы всеми предприятиями региона может оказаться, что регион в целом с программой не справился. Этот вопрос подробнее освещен в п. 10.7. 10.6. Построение индексов при обобщении данных по единицам совокупности и по элементамМы обсудили построение индексов при обобщении данных по многим товарам или «элементам» и при обобщении данных по единицам при наличии одного элемента (одного вида товара). В экономических расчетах приходится иметь дело с задачами построения индексов, объединяющих данные по единицам и по элементам. Обозначим число элементов т, число единиц п. Обобщение данных при построении индексов можно подразделить на три уровня: 1) п = 1, т > 1- индексный анализ проводится по одной единице (предприятию, магазину и т.д.) и группе элементов; 2) п > 1, т = 1 - индексный анализ по группе единиц и одному элементу (товару, виду продукции); 3) п > 1, т > 1— индексный анализ по группе единиц и элементов.
Продолжение
Последний тип задач характерен для муниципального управления, аналитической работы в региональных, ведомственных и федеральных статистических службах. Предположим, нам нужно изучить потребление продовольствия в районе города. Собраны данные об объеме покупок товаров и ценах на рынках и в приватизированных магазинах (табл. 10.7). По данным табл. 10.7 можно построить индексы объема продажи и цен для каждого вида торговли в отдельности, что соответствует данным типа 1; можно определить изменение объема продажи и цен на каждый из товаров по всем видам торговли, что соответствует данным типа 2; наконец, можно получить индексы объема продаж и цен по всем видам торговли и всем товарам. Произведем последовательно расчеты всех индексов, используя базисные веса в индексах объема и отчетные - в индексах цен. Рынок. Магазин I. В этом магазине ассортимент товаров изменялся: в базисном периоде говядины не было в продаже, в отчетном - она появилась. В этом случае изменение цен определяется по сопоставимому кругу товаров, т.е. по четырем товарам. Обозначим сопоставимый круг товаров l, полный круг в базисном периоде – m0, в отчетном – m1. Тогда Индекс объема продаж должен отразить изменение объема продаж тех товаров, которые были в базисном и продолжали продаваться в отчетном периоде, и, кроме того, изменение в объеме продажи в связи с появлением нового товара (несопоставимого). Так что
т. е. этот индекс должен включать данные по полному кругу элементов (товаров): сопоставимым и несопоставимым. В нашем примере •
Возникает проблема определения базисной цены для товара, который имелся только в отчетном периоде. Возможны по крайней мере три ее решения. 1. Использование для несопоставимых элементов цены отчетного периода, т. е. числитель 1q представляется как По данным табл. 10.7 Расчет 1q этим методом нарушает увязку индексов в систему: 1,21·1,583 = 1,9154·100% = 191,54%, тогда как по данным табл. 10.7 индекс выручки составил:
Однако выполняется увязка абсолютных изменений: Δw = Δqp =Δqp0 + Δpq1 = (80,00 - 50,55) + (53,25 - 44,00) = 38,70 тыс. руб.; если сравним непосредственно суммы выручки отчетного периода, то получим ту же величину: Δw = 89,25 - 50 55 = 38,70 тыс. руб. 2. Использование условных значений базисных цен, которые определяются расчетным путем. Логично предположить, что если бы говядина была в базисном периоде, то цены на нее повысились примерно так же, как и на остальные товары. Это предположение, можно записать в виде равенства: Так как
В нашем примере условная цена говядины в магазине 1 в базисном периоде составила 3. Использование базисных цен других едивиц или средних по совокупности. Например, при расчете / для магазина 1 использовать базисную цену на говядину в магазине 2. Тогда В данном случае из-за совпадения рг0 в магазине 2 с рu1 в магазине 1 этот метод привел к тому же результату, что и первый. Использование средней базисной цены на говядину по всем видам торговли дает менее реальные результаты ввиду того, что значительный объем продаж говядины осуществляется на рынке, где цены были выше. Поэтому р̅г > р̅г0. Значение индекса объема продаж составило: Это значение превышает все предыдущие. Магазин 2. Здесь тоже ассортимент менялся: в отчетном периоде не торговали сахарным песком. Но это не вызывает трудностей в построении индексов, так как изменение объема продаж обусловлено как изменением продаж сопоставимых товаров, так и отсутствием продажи несопоставимого товара.
Если нужно рассчитать q0p1 для несопоставимого товара, то можно воспользоваться одним из рассмотренных способов. Чтобы получить результаты по всем видам торговли, данные обобщаются определенным образом. При этом возможны два подхода. Первый подход основан на суммировании данных по видам торговли (или отдельным предприятиям). Этот метод основан на данных отдельных хозяйственных единиц и поэтому называется заводским методом.
где п - число единиц совокупности; т — число элементов, всего; l - число сопоставимых элементов. В этом случае один и тот же товар или вид продукции взвешивается по разным ценам в зависимости от того, где он учитывается. Второй подход основан на обобщении данных по отдельным товарам независимо от места реализации. Рассчитываются для каждого товара сводные показатели количества и цены:
Затем данные обобщаются по всем товарам, при этом каждый из них взвешивается по средней цене для данного товара. Этот метод основан на обобщении с позиций совокупности, а не отдельных единиц и потому получил название отраслевой метод:
При этом сопоставимость элементов определяется, исходя из условий совокупности в целом. В нашем примере (табл. 10.7) были товары, не сопоставимые с позиций отдельных видов торговли, но в целом для торговли все они сопоставимы. Вычислим индексы тем и другим методом: по данным отдельных видов торговли
по данным всех видов торговли, вместе взятых,
Получилось, что средние цены повысились в меньшей степени, чем в отдельных видах торговли: +8,4% против +14,5%. Это соотношение отражает влияние структурного фактора, изменение удельного веса продажи того или иного товара разными видами торговли. В частности, большое значение имела продажа говядины в отчетном периоде не только на рынке и в магазине 1, но и в магазине 2, где цены ниже. Соотношение индекса средних цен и индекса цен без учета структурного фактора дает оценку структурных сдвигов:
т. е. за счет изменения соотношения разных видов торговли в общем объеме реализации средние цены снизились на 5,9%. Мы получили индекс структуры исходя из взаимосвязи индексов. Можно рассчитать его значение непосредственно по формуле
Если стоит задача измерить влияние объема продаж на величину выручки от продажи, т. е. найти Iw(q), то это влияние измеряет индекс, найденный по заводскому методу. Его величина отражает одновременно и изменение объема продажи во всех видах торговли, и изменение структуры продажи. Алгебраически это можно представить в виде равенства: где По данным табл. 19.7 IQ = 1,108 , Iq = 1,108·0,941 = 1,042·100% = 104,2%. Мы рассмотрели систему индексов, в которой использовались разновзвешенные индексы: индексы объемного фактора (количества) с базисными весами, индексы качественного фактора (цен) - с отчетными весами. Плюсы и минусы такого метода построения индексов уже обсуждались. Если необходимо все индексы построить на базисных весах, то в системе индексов появляется индекс совместных изменений. С экономической точки зрения его часто называют индексом смещения ассортимента, так как он показывает изменение в реализации доли товаров с разным темпом снижения цен:
Можно оценить эффект совместного изменения признаков q и р в системе индексов, построенных по заводскому методу:
Вполне возможны различия в значениях индексов совместных изменений, полученных по формуле (10.36) или (10.37). Это различие может возникнуть из-за разного охвата элементов: в первом случае сопоставимость определяется с общеотраслевых позиций, во втором - с позиций отдельного предприятия. Итак, вы получили представление о способах построения индексов при обобщении данных и по многим товарам, видам продукции и по магазинам, рынкам, предприятиям. Какой метод выбрать в каждом конкретном случае, вам часто придется решать самим, ведь далеко не всегда имеется инструкция по проведению расчетов. 10.7. Границы и условия применения индексного методаКаждый метод ориентирован на особые представления изучаемого объекта, на особую его модель. Индексный метод предполагает, что связь между признаками является жестко детерминированной, которая проявляется как в каждом отдельном случае (для отдельного товара, вида продукции, предприятия и т. д.), так и в совокупности. Связь, изучаемая с помощью индексов, выражается в виде уравнения связи: либо мультипликативного у = х1x2...хk либо аддитивного у = х1 + х2 + ... + хk, Вид функции, число переменных факторов (сомножителей или слагаемых) определяются нашими представлениями о логике изучаемой связи. Многофакторная мультипликативная модель строится путем последовательного расчленения одного из факторов на составляющие. Например, можно записать следующее уравнение связи:
Эту модель можно детализировать. Она будет включать не два, а пять факторов:
Если мультипликативная модель имеет в качестве результативного первичный признак, то она называется полной. Примером такой модели является вышеуказанная модель. Разделив обе части равенства на первый фактор, получим неполную модель среднечасовой выработки работника. Представление связи как жестко детерминированной является условным, так как связи социально-экономических явлений носят стохастический характер. Если представить мультипликативную модель как двухфакторную, т.е. у = x1x2, то в целом по совокупности уравнение имеет вид у = ах. Коэффициент а является коэффициентом связи между у и х. Он передает прямое влияние фактора х на результат у. Для нашего примера величина отработанных человеко-часов передает влияние среднечасовой выработки на объем продукции. Однако выработка влияет на результат не только непосредственно, но и через другие факторы: уровень выработки может определять численность рабочих, их долю в списочном составе, фактическую продолжительность рабочего дня. В корреляционном анализе, измеряя корреляцию между результатом и фактором, мы получаем полную меру корреляции независимо от того, как реализуется связь — непосредственно или опосредованно. В индексном анализе мы измеряем только прямое влияние изменения фактора на изменение результата. При построении уравнения связи иногда допускаются отступления от логики ради обеспечения увязки признаков, получения жестко детерминированного выражения связи. Поэтому можно встретить уравнения связи, в которых не все составляющие элементы экономически обоснованы, нередки случаи появления среди факторов обратных величин. Приведем пример недостаточно обоснованного уравнения связи:
Трудно представить, чтобы рост доли основных фондов вызывал рост балансовой прибыли. При мультипликативной связи индексов относительные выражения приростов факторов связаны аддитивно. Например,
Чем больше различаются индексы отдельных факторов, тем больше сумма относительных приростов отличается от темпа прироста результата. Например, Если известно, что значение первого индекса 1,2, второго - 1,05, то
т. е. переход от темпов роста к темпам прироста приводит к определенным трудностям в интерпретации количественного влияния факторов на результат. Наконец, решение вопроса об измерении эффекта отдельных факторов и их совместного изменения всегда условно. Все предыдущее изложение было ориентировано на мультипликативную модель. При аддитивной связи признаков индексный анализ проводится по следующей формуле:
т. е. общее изменение результата зависит от изменения каждого фактора и его доли в базисной величине результата. Приведем пример (табл. 10.8). Таблица 10.8 Численность работников на заводе
Общее изменение численности работников может быть представлено как результат изменения численности занятых умственным и физическим трудом и их доли в общей численности работников:
Этот результат отличается от 0,8 (800 : 1000) только за счет округления в расчетах. Одним из сложнейших вопросов индексного анализа является оценка структурных сдвигов. Этот фактор может приводить к парадоксальным результатам в индексах. Возьмем для примера условные данные о работе трех химических предприятий одного района (табл. 10.19). Таблица 10.9 Показатели работы химических предприятий района
На каждом из этих предприятий рост объема производства сопровождался повышением производительности труда. Средняя выработка на одного работника по предприятиям составила в отчетном квартале соответственно 12,6 тыс. руб., 21,26 тыс. руб. и 50,40 тыс. руб. В прошлом квартале средняя выработка составляла 12 тыс. руб., 20,25 тыс. руб. и 48 тыс. руб. Сравнение этих данных показывает, что выработка росла равномерно на всех предприятиях: на первом заводе (12,6 : 12 = 1,05, или 105%); на втором -(21,26 : 20,25 = 1,0498, или 104,98%); на третьем - (50,4 : 48 = 1,05, или 105%). Если рассчитать среднюю выработку по всем трем заводам и определить ее динамику, то результат покажется невероятным. В отчетном квартале средняя выработка в целом составила 15,92 тыс. руб. (65282 тыс. руб. : 4100 чел.), а в прошлом квартале - 18,075 тыс. руб. (36150 тыс. руб.: 2000 чел.), т. е. средняя выработка по отрасли снизилась на 12% (15,92 тыс. руб. : 18,075 тыс. руб. = 0,88·100% = 88%). Этот результат объясняется тем, что динамика среднеотраслевой выработки учитывает не только, какой была динамика выработки на отдельных предприятиях, но и как изменялось распределение работников между ними. Ведь уровень средней выработки на одного работника на отдельных предприятиях различается достаточно сильно: максимален он на заводе пластиков, минимален — на заводе минеральных удобрений. Именно на этом заводе численность работников возросла почти в 3 раза. Доля этого завода в численности работающих составляла 60% в прошлом квартале и 78,1% - в отчетном квартале. Отсюда и совокупный результат. Можно измерить общее изменение выработки без учета изменения соотношений между предприятиями: если сравнить общий объем товарной продукции в сопоставимых ценах в отчетном квартале с тем объемом, который был бы получен, если бы выработка на каждом заводе оставалась прежней. Величина такой «условной» товарной продукции составит: 12 тыс. руб. 3200 чел.+ 20,25 тыс. руб. × 700 чел. + 50,4 тыс. руб. × 200 чел.= 62175 тыс. руб. Суммарные показатели товарной продукции 65282 тыс. руб. и 62175 тыс. руб. различаются только за счет выработки, значит их сравнение покажет динамику средней выработки по всем трем предприятиям без учета динамики численности работников. Действительно, получаем, что и в целом рост выработки составил +5% (65282 тыс. руб : 62175 тыс. руб. = 1,05, или 105%). Вот теперь нет никакого противоречия между результатами работы отдельных предприятий и отрасли. Но чтобы разобраться в этом, нужно знать, какой методикой пользовался статистик, как он получил те или иные результаты. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

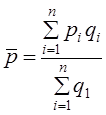
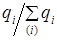 - структура продажи.
- структура продажи.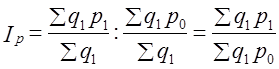
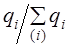 . На основе индекса средней величины могут быть построены индекс самого осредняемого признака при постоянстве структуры совокупности и индекс структуры:
. На основе индекса средней величины могут быть построены индекс самого осредняемого признака при постоянстве структуры совокупности и индекс структуры: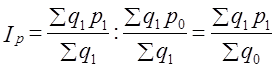 (10.23)
(10.23)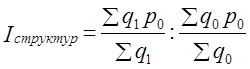 (10.24)
(10.24)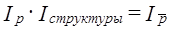 или
или 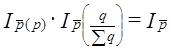 (10.25)
(10.25)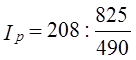 = 1,235·100% = 123,5%,
= 1,235·100% = 123,5%,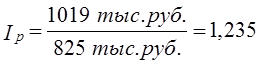
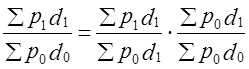 (10.26)
(10.26)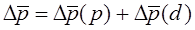 (10.27)
(10.27)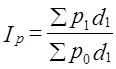 и
и 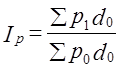
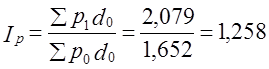


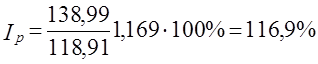
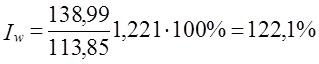
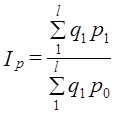 (10.28)
(10.28)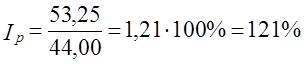

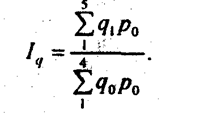
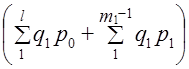
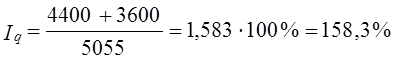
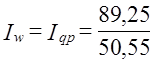 = 1,7656·100% = 176,6%.
= 1,7656·100% = 176,6%.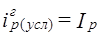
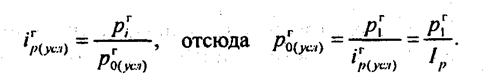
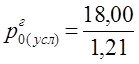 =14,876 тыс. руб./кг. Тогда
=14,876 тыс. руб./кг. Тогда 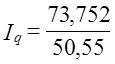 =1459.100% = 145,9%. Обратим внимание на то, что этот метод обеспечивает увязку индексов в систему, т. е. 1q· Ip = Iqp или Iw = 1,459·1,21 = 1,765. Однако взаимосвязь абсолютных изменений не выполняется: (73,752 - 50,55) + (53,25 - 44,00) = 23,202 + 9,25 = 32452 тыс. руб. вместо фактической величины изменения 38,70 тыс. руб.
=1459.100% = 145,9%. Обратим внимание на то, что этот метод обеспечивает увязку индексов в систему, т. е. 1q· Ip = Iqp или Iw = 1,459·1,21 = 1,765. Однако взаимосвязь абсолютных изменений не выполняется: (73,752 - 50,55) + (53,25 - 44,00) = 23,202 + 9,25 = 32452 тыс. руб. вместо фактической величины изменения 38,70 тыс. руб.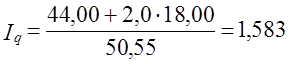
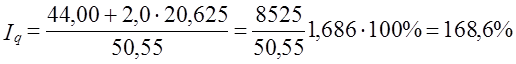
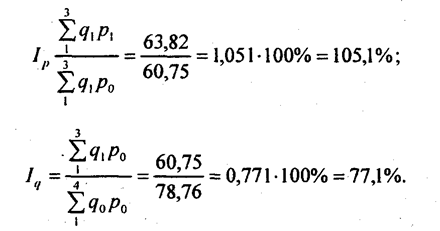
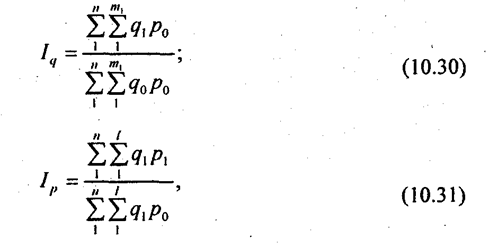
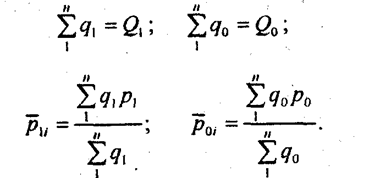
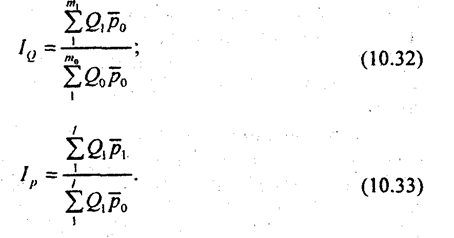
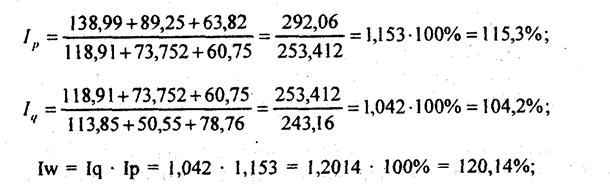
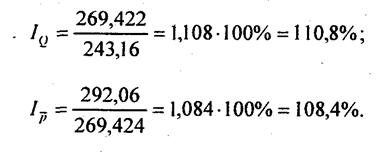
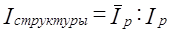 = 1,084 : 1,153 = 0,941·100% = 94,1%,
= 1,084 : 1,153 = 0,941·100% = 94,1%,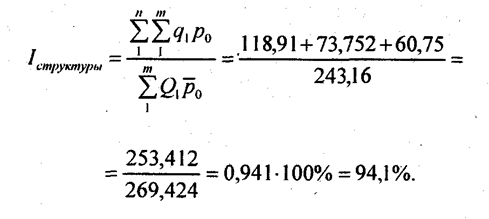
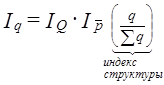 (19.34)
(19.34)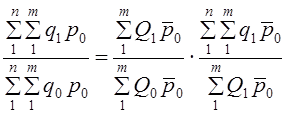 (10.35)
(10.35)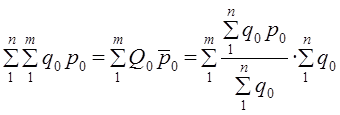
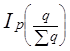 = 0,941, тогда
= 0,941, тогда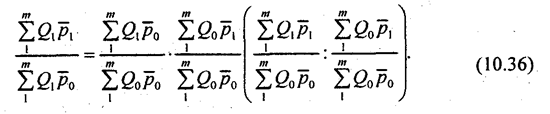
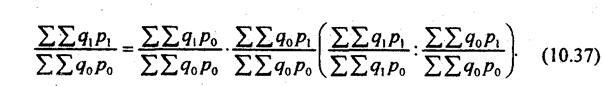
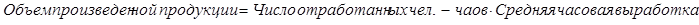

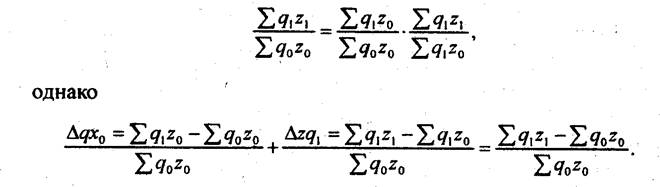
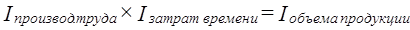
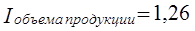 , тогда как
, тогда как 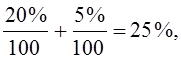
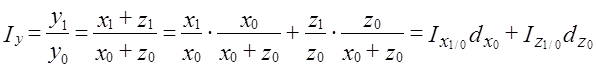 ,
,