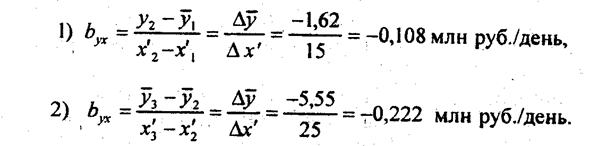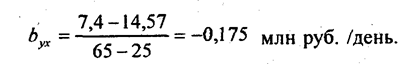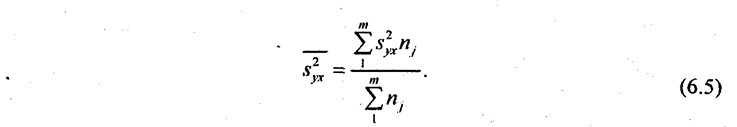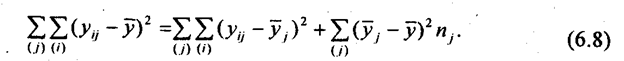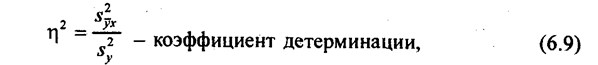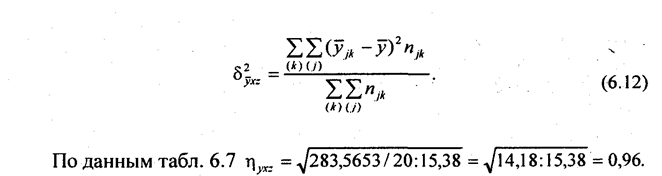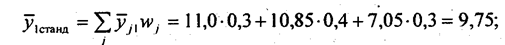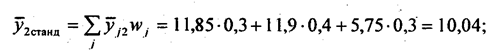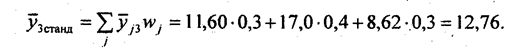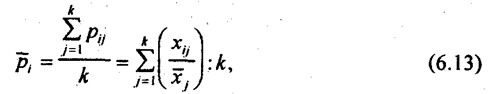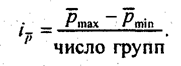| Главная » Учебно-методические материалы » СТАТИСТИКА » Общая теория статистики: учебник. Под ред. Елисеевой И.И. |
| 23.01.2012, 11:40 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
6.1. Значение и сущность группировкиРусский статистик Д. П. Журавский (1810 - 1856) очень точно определил статистику как «счет по категориям». Действительно, среди бесконечного разнообразия явлений мы, как правило, улавливаем наличие некоторого конечного числа групп или типов. Лицо каждого человека неповторимо, и все-таки можно классифицировать лица по типам (скуластое, продолговатое, круглое и т.д.); предприятия образуют группы по формам собственности, характеру производимой продукции, размерам (крупные, средние, мелкие), финансовому положению; государства делятся на группы по уровню экономического развития и т.д. Примеры можно продолжить, но ясно, что какую бы совокупность мы не изучали, она всегда подразделяется на группы. Это обусловлено такими объективными свойствами явлений, как вариация, наличие частных совокупностей (см. гл. 1). Группировка - это распределение единиц по группам в соответствии со следующим принципом: различия между единицами, отнесенными к одной группе, должны быть меньше, чем между единицами, отнесенными к разным группам. Группировка лежит в основе всей дальнейшей работы с собранной информацией. На основе группировки рассчитываются сводные показатели по группам, появляется возможность их сравнения, анализа причин различий между группами, изучения взаимосвязей между признаками. Если рассчитать сводные показатели только в целом по совокупности, то мы не сможем уловить ее структуры, роли отдельных групп, их специфики. Однородность (гомогенность) данных является исходным условием их статистического описания и анализа - вычисления и интерпретации обобщающих показателей, построения уравнения регрессии, измерения корреляции (см. гл. 8), статистического умозаключения (см. гл. 7).. Таким образом, значение группировки состоит в том, что этот метод обеспечивает обобщение данных, представление их в компактном, обозримом виде. Кроме того, группировка создает основу для последующей сводки и анализа данных. Для изучения структурных изменений в экономике государственная статистика использует группировку хозяйственных субъектов по формам собственности и организационно-правовым формам, представленную в табл. 6.1. Сводные показатели для отдельных групп являются типичными и устойчивыми, если, во-первых, группировка проведена правильно, во-вторых, группы имеют достаточную численность. Первое условие связано с тем, что деление на группы далеко не всегда очевидно. Выполнение второго условия необходимо, так как при достаточно большом числе единиц (не менее 5 единиц в группе) в сводных показателях взаимопогашаются случайные характеристики и проявляются закономерные, типичные. Для решения задачи группировки нужно установить правила отнесения каждой единицы к той или иной группе. В эти правила входят определения тех характеристик (признаков), по которым будет проводиться группировка (так называемых группированных признаков), и их значений, отделяющих одну группу от другой (интервалов группировки). Группировка называется простой (монотетической), если для ее построения используется один группировочный признак. Если группировка проводится по нескольким признакам, она называется сложной (политетической). Обычно такая группировка проводится как комбинационная, т.е. группы, выделенные по одному признаку, подразделяются на подгруппы по другому признаку. Казалось бы, этот метод выделения групп должен быть лучше простой группировки - ведь трудно ожидать, что различия между группами можно уловить лишь на основе одного признака. Однако комбинация признаков приводит к дроблению совокупности в геометрической прогрессии: число групп будет равно произведению числа группировочных признаков (l) на число выделенных категорий по каждому из них (т): k = l∙ т. Данные становятся труднообозримыми, группы включают малое число единиц, групповые показатели становятся ненадежными. Альтернативой является проведение многомерных группировок или многомерных классификаций (см. п. 6.3). Остановимся на определении интервалов группировочных признаков. Используются интервалы открытые и закрытые. В первом случае указываются верхняя и нижняя границы интервала. Например, группы предприятий по численности работников, человек: 200 - 600, 600 - 1000, 1000 - 2000. Такая запись предполагает, что единица, у которой значение признака совпадает с верхней границей интервала, относится к следующей группе, т.е. интервал читается как «от - до». Иногда границы закрытых интервалов предполагают включение единиц с нижней и верхней границами. Например, группировка населения по возрасту, лет: 0-4,5-9,10-14,15-19,20-24, 25-29 и т.д. Интервал называется открытым, если указана либо только верхняя, либо только нижняя граница: до 200 человек или 2000 человек и более. Закрытые интервалы подразделяются травные и неравные. Как указывалось в гл. 5, величина равного интервала находится по формуле
Неравные интервалы могут определяться как равнонстолненные. При этом совокупность разделяется на группы равного объема с числом единиц в каждой j-й группе: пj = п: т, где п - общее число единиц; т - число групп. Данные ранжируются, отсчитывается число единиц, составляющих первую группу n1, затем - вторую п2 и т.д. Границы интервалов будут соответствовать фактическим значениям признака в каждой группе. Таблица 6.1 Организационно-правовые формы и формы собственности хозяйственных субъектов Российской Федерации Бывает, что число групп заранее неизвестно и определяется опытным путем на основе перебора вариантов группировки, выявления такого варианта, который наилучшим образом позволяет увидеть различия между группами. При определении числа групп следует обращать внимание на то, чтобы в одну группу не попало бы свыше половины всех единиц совокупности и в средних группах было больше единиц, чем в крайних. Если группировочный признак неколичественный, или количественный дискретный с малым числом значений, то группировка данных производится путем подсчета числа единиц с данным значением признака. Примером такой группировки является табл. 6.2. Таблица 6.2 Группировка станкостроительных заводов по числу производимых типов станков
Очевидно, что метод группировок тесно связан с представлением данных в виде групповых или комбинационных таблиц, а также с графическим представлением структуры совокупности ее частей и соотношений между ними. 6.2. Виды группировокГруппировка производится с целью установления статистических связей и закономерностей, построения описания объекта, выявления структуры изучаемой совокупности. Различия в целевом назначении группировки выражаются в существующей в отечественной статистике классификации группировок: типологические, структурные, аналитические. Типологическая группировка служит для выделения социально-экономических типов. Этот вид группировок в значительной степени определяется представлениями экспертов о том, какие типы могут встретиться в изучаемой совокупности. Чтобы пояснить особенность этой группировки, остановимся на последовательности действий для ее проведения: 1) называются те типы явлений, которые могут быть выделены; 2) выбираются группировочные признаки, формирующие описание типов; 3) устанавливаются границы интервалов; 4) группировка оформляется в таблицу, выделенные группы (на основе комбинации группировочных признаков) объединяются в намеченные типы, и определяется численность каждого из них. Рассмотрим пример. Поставлена задача выделить типы акционерных компаний с высокими, средними и низкими дивидендами и установить распространенность каждого типа в данном регионе. Показатель выплаты дивидендов характеризует долю прибыли на акцию или долю чистого дохода, выплачиваемого как дивиденды.
Этот коэффициент зависит от структуры акционерного капитала фирмы, длительности существования фирмы и перспектив ее роста. Обычно молодые, быстрорастущие компании выплачивают низкие дивиденды, если вообще их выплачивают; тогда как зрелые компании стремятся дать более высокие дивиденды. Структура капитала и выплата дивидендов зависят от отраслевой принадлежности фирмы. Поэтому при классификации фирм по уровню выплаты дивидендов мы должны использовать в качестве группировочных признаков, во-первых, отрасль (подотрасль), во-вторых, показатель выплаты дивидендов. Первый группировочный признак выполняет роль характеристики условий, второй непосредственно характеризует тип фирмы. Границы интервалов для второго группировочного признака могут изменяться при переходе от одной отрасли к другой, так как то, что для одной отрасли может рассматриваться как высокий уровень выплаты, для другой может оцениваться иначе. Изменение границ интервалов группировочного признака при выделении одних и тех же типов в разных условиях называется специализацией интервалов группировочного признака. Иногда условия формирования типов приводят к различиям в их описании, в самом круге признаков. Например, выделение крупных, средних, мелких предприятий в разных отраслях должно производиться по разным характеристикам: в энергоемких отраслях - по потреблению электроэнергии; в сырьеемких - по величине товарно-материальных запасов; в трудоемких — по численности рабочих; в капиталоемких - по стоимости оборудования. Изменение круга группировочных признаков при выделении одних и тех же типов в разных условиях называется специализацией группировочных признаков. Вернемся к нашему примеру. Предположим, что мы располагаем данными 15 фирм, представляющих три подотрасли промышленности. Проведем их группировку с учетом двух выше названных признаков (табл. 6.3). В табл. 6.3 (гр. В) для краткости использованы условные обозначения типов компаний: н - компании с низким показателем выплаты дивидендов, с - средним, в - высоким показателем выплаты. Таблица 6.3 Группировка акционерных компаний п-гс района по уровню выплаты дивидендов за 19_ г.
Использование специализации интервалов как бы уравнивает наши оценки компаний в разных отраслях, что позволяет объединить выделенные группы в три типа независимо от отрасли (табл. 6.4). Это последний шаг типологической группировки. Как видим, этот метод группировки позволяет избавиться от чрезмерного дробления совокупности, но он слишком субъективен: эксперт определяет, какие типы должны быть выделены, по каким признакам, какими должны быть границы интервалов. К тому же число группировочных признаков ограничено двумя-тремя. Однако, если объект исследования хорошо изучен, если имеется развитая теория, то этот метод может дать хорошо интерпретируемые результаты. Таблица 6.4 Распределение акционерных компаний л-го района по уровню выплаты дивидендов в 19 г.
В любом случае правильность проведения типологической группировки требует проверки. С этой целью рассчитываются сводные показатели' по группам (средние, относительные величины); если различие между группами статистически незначимо (по /-критерию Стьюдента или F-критерию, или критерию /2 и т.д., см. гл. 7), то схема группировки должна быть пересмотрена - схожие группы могут быть объединены, изменены границы интервалов и т. д. Таблица 6-5 Распределение населения Российской Федерации по среднедушевому денежному доходу* (%)
Структурная группировка характеризует структуру совокупности по какому-либо одному признаку. Пример такой группировки представлен в табл. 6.5. Если для типологической группировки чаще используются открытые и неравные ин-тервалы, то для структурной группировки более характерны закрытые равные интервалы. Структурная группировка позволяет изучать интенсивность вариации группировочного признака (см. гл. 5). На основе структурной группировки можно изучать динамику структуры совокупности. Если известны структурные характеристики совокупности в одном и другом периодах: wi0 и wi1 – доли i-й группы в период «0» и в период «1», то можно рассчитать показатель среднего абсолютного изменения структуры:
где k — число групп. Другой сводный показатель абсолютных структурных сдвигов строи гся на основе формулы среднего квадратического отклонения:
Если показатели структуры выразить не в долях, а в процентах, то, так же как и первый показатель, квадратичный коэффициент абсолютных структурных сдвигов оценивает на сколько процентных пунктов в среднем различаются удельные веса отдельных групп сравниваемых структур. При отсутствии структурных сдвигов оба эти показателя равны нулю; их величина тем больше, чем значительнее абсолютные изменения удельных весов групп. Квадратичный коэффициент более чутко реагирует на структурные изменения. Существуют и другие показатели для измерения структурных сдвигов (см., например, индекс структуры в гл. 10). При сравнениях предполагается, что число групп в одном и другом периодах остается одним и тем же. По данным табл. 6.5,
Деление группировок на типологические и структурные достаточно условие. Если задать, например, границы среднедушевого дохода, соответствующие определенным типам благосостояния, то можно с полным правом назвать группировку типологической. Аналитическая группировка характеризует взаимосвязь между двумя и более признаками, из которых один рассматривается как результат, другой (другие) — как фактор (факторы). Пример однофакторной аналитической группировки представлен в табл. 6.6. В данном примере оборачиваемость в днях - фактор, обозначенный х, прибыль - результат - у. Очевидно, что при одном и том же сроке оборота предприятия могут иметь разную прибыль. Чтобы установить связь между признаками, данные группируются по признаку-фактору. Затем по каждой группе рассчитывается среднее значение результата. По обобщенным данным гораздо легче увидеть, есть связь между признаками или нет, прямая связь или обратная, линейная или нелинейная. Эти выводы делаются через сопоставление изменений средних значений результата по группам с изменениями фактора. Чтобы эти изменения были сравнимыми, следует проводить группировку с равными интервалами или рассчитывать изменения результата наединицу изменений фактора. Таблица 6.6 Характеристика зависимости прибыли малых предприятий от оборачиваемости оборотных средств за 19_ г.
В примере средняя прибыль изменяется от группы к группе, следовательно, связь между оборачиваемостью и прибылью существует, причем обратная: чем медленнее оборачиваются оборотные средства, тем меньше прибыль. Рассчитаем, насколько снижается прибыль при замедлении оборачиваемости от 40-50 до 51-70 дней и при замедлении оборачиваемости от 51-70 до 71-101 дня:
Полученные значения показывают величину снижения прибыли при замедлении оборачиваемости на 1 день. Такие показатели называются показателями силы связи. Различие в их значениях свидетельствует, что сила влияния оборачиваемости на прибыль не является постоянной - она возрастает при сроках оборачиваемости свыше 50 дней, т.е. связь признаков нелинейная. В случае линейной связи важным показателем является характеристика средней силы связи:
где y̅m, y̅l - средние значения результативного признака в последней и первой группах соответственно; х'm, x’l - середины интервалов (или средние значения) факторного признака в последней и первой группах. В случае прямой связи byx > 0, обратной – byx < 0. По данным табл. 6.5
Для нелинейной связи показатель средней силы связи не имеет значения (или имеет ограниченное значение). По аналитической группировке можно измерить связь с помощью еще одного показателя: эмпирического корреляционного отношения. Этот, показатель обозначается греческой буквой h (эта). Он основан на правиле разложения дисперсии, согласно которому общая дисперсия s2 равна сумме внутригрупповой и межгрупповой дисперсий. Дисперсия результативного признака внутри группы при относительном постоянстве признака-фактора возникает за счет других факторов (не связанных с изучаемым). Эта дисперсия называется остаточной (та колеблемость, которая осталась при закреплении изучаемого фактора х). Она определяется по формуле:
где уij - значение признака у для i-й единицы в j-й группе; у̅j - среднее значение признака у ву-й группе; nj - число единиц ву-й группе; j = 1, 2, 3, ..., т. Внутригрупповые дисперсии, рассчитанные для отдельных групп, объединяются в средней величине внутригрупповой дисперсии:
Межгрупповая дисперсия относится на счет изучаемого фактора (и факторов, связанных с ним), поэтому эта дисперсия называется факторной. Она определяется по формуле
Правило сложения дисперсий может быть записано:
или
Эмпирическое корреляционное отношение измеряет, какую часть общей колеблемости результативного признака вызывает изучаемый фактор. Соответственно оно рассчитывается как отношение факторной дисперсии к общей дисперсии результативного признака:
Этот показатель принимает значения в интервале [0,1]: чем ближе к 1, тем теснее связь, и наоборот. По данным табл. 6.6 этот показатель равен h = 0,881, связь тесная. Для изучения влияния нескольких факторов на результат проводится многофакторная аналитическая группировка. Она строится как комбинационная группировка по признакам-факторам, и для каждой подгруппы рассчитывается среднее значение результативного признака. Обратимся к рассмотренному выше примеру, который дополним вторым фактором формирования прибыли - величиной запаса оборотных средств (г); по этому фактору выделены три группы (табл. 6.7). Таблица 6.7 Характеристика зависимости прибыли малых предприятий от величины запаса и оборачиваемости оборотных средств за 19_ г.
Эта группировка позволяет проследить колеблемость прибыли под влиянием двух факторов. Конечно, уверенность нашего заключения е, том, что прибыль изменяется от группы к группе именно за счет изменений запаса оборотных средств и скорости их обращения, зависит от того, насколько обеспечено погашение влияния прочих факторов, т.е. от числа единиц в подгруппах (Ид). В данном примере наполненность групп недостаточна для того, чтобы выявить «чистое» влияние изучаемых факторов. При njk > 5 многjфакторная аналитическая группировка позволяет измерить силу связи между результатом и одним из факторов при постоянстве второго фактора, т.е. получить так называемые частные (или чистые) показатели силы связи. По данным табл. 6.7 рассчитаны показатели силы связи между прибылью и оборачиваемостью при закреплении уровня запасов оборотных средств. Таких показателей три (по числу групп по фактору z):
Точно так же могут быть вычислены показатели силы связи между прибылью и запасом оборотных средств при закреплении оборачиваемости:
Чистое влияние первого фактора (обратное) возрастает при увеличении уровня закрепленного фактора (величины запасов оборотных средств), а второго - снижается. Можно рассчитать и показатель множественной тесноты связи -совокупное эмпирическое корреляционное отношение. Для трех признаков, как в нашем примере, его формула следующая: .
Так же как и показатель парной связи, hxyz принимает значение в интервале [0,1]. В числителе подкоренного выражения находится факторная дисперсия результативного признака:
Можно с некоторыми оговорками заключить, что на 92% (0,962) вариация прибыли в этой совокупности предприятий определяется вариацией изучаемых факторов. Многофакторная аналитическая группировка — очень гибкий прием изучения связей. Она позволяет уловить влияние факторов на результат с изменением условий (закреплением прочих факторов на разных уровнях). Однако при всех отмеченных плюсах этот метод имеет огромный минус - дробление совокупности, в результате чего выделяются подгруппы с малым числом единиц. В этом случае средние значения результативного признака неустойчивы, не достигается погашение прочих факторов, соответственно, ненадежными становятся и показатели связи. Но если совокупность большого объема и распределение признаков-факторов не являются крайне асимметричными, этот метод, как никакой другой, позволяет получить много информации об отношениях между переменными. В какой-то мере избежать дробления данных и при этом получить «чистые» характеристики связей между переменными позволяет применение метода стандартизации распределений в комбинационной таблице. Если в группах по одной переменной, скажем, по г в табл. 6.7, распределение по другой переменной х принять стандартным и на его основе рассчитать групповые средние величины результативного признака, то они будут отличаться за счет принадлежности к разным группам по признаку z при элиминировании признака х. В качестве стандартного применяется распределение в целом по совокупности. Так, по данным табл. 6.7 стандартное распределение по х следующее: x1 - 6 ед., х2 - 8 ед., х3 - 6 ед. или в относительном выражении: 0,3; 0,4; 0,3. Тогда средняя прибыль при заданном значении переменной z при стандартизации распределения по переменнбй х равна: в первой группе:
во второй группе:
в третьей группе:
На основе полученных стандартизованных средних можно рассчитать показатели «чистой» связи между величиной прибыли и средним запасом оборотных средств. Попробуйте сделать такой расчет. Стандартизация распределения по переменной z, расчет стандартизованных средних результативного признака и показателей «чистой» связи между у и х при элиминировании z проводится аналогично. Заметим, что рассмотренные приемы анализа не входят пока в ППП для ЭВМ. Возможно, это сделает кто-то из вас. 6.3. Многомерные группировкиМы убедились, как трудно выбрать какой-то один признак в качестве основания группировки. Еще труднее проводить группировку по нескольким признакам. Комбинация двух признаков позволяет сохранить обозримость таблицы, но комбинация трех или четырех признаков дает совершенно неудовлетворительный результат: ведь даже при выделении трех категорий по каждому из груп-пировочных признаков мы получим 9 или 12 подгрупп. Равномерность распределения единиц по группам в принципе невозможна. Вот и получаются группы, в которые входят 1-2 наблюдения. Сохранить сложность описания групп и вместе с тем преодолеть недостатки комбинационной группировки позволяют методы многомерных группировок. Часто их называют методами многомерной классификации. Эти методы получили распространение благодаря использованию ЭВМ и пакетов прикладных программ. Цель этих методов — классификация данных, иначе говоря, группировка на основе множества |Признаков. Такие задачи широко распространены в науках о приро-|де и обществе, в практической деятельности по управлению массо-^Яыми процессами. Например, выделение типов предприятий по Ижнансовому положению, по экономической эффективности деятельности производится на основе множества признаков: выделение и изучение типов людей по степени их пригодности к определенной профессии (профпригодность); диагностика болезней на основании множества объективных признаков (симптомов) и т. д. Простейшим вариантом многомерной классификации является группировка на основе многомерных средних. Многомерной средней называется средняя величина нескольких признаков для одной единицы совокупности. Поскольку нельзя рассчитать среднюю величину абсолютных значений разных признаков выраженных в разных единицах измерения, то многомерная средняя вычисляется из относительных величин, как правило, - из отношений значений признаков для единицы совокупности к средним значениям этих признаков:
где p̅j - многомерная средняя для i-единицы; хij - значение признака х, для г-единицы; хj - среднее значение признака xi, k - число признаков; j - номер признака; i - номер единицы совокупности. Рассмотрим использование многомерных средних на примере сельскохозяйственных предприятий Всеволожского района Ленинградской области за 1995 г. (табл. 6.8). По каждому предприятию приведены четыре признака: • среднемесячная оплата труда работника, руб., x1; • валовой доход на 1 га сельхозугодий, тыс. руб./га, х2; • среднегодовая стоимость основных производственных фондов на 1 га сельхозугодий, млн руб./га, x3; • отношение дебиторской задолженности к кредиторской задолженности, %, x4. Эти признаки можно считать однородными, так как большая их величина положительно характеризует экономику предприятия. Предпочтительнее обобщать в многомерной средней признаки либо «положительные», либо «отрицательные» (чем больше, тем хуже). Многомерные средние, приведенные в последней графе табл. 6.8, обобщают четыре признака.. При этом значимость признаков для оценки предприятия полагается одинаковой, что, конечно, спорно. Можно .усложнить методику, приписав признакам, на основе экспертнои оценки, разные веса, и вычислить взвешенные многомерные средние. Таблица 6.8 Характеристики предприятий Всеволожского района Ленинградской области в 1995 г.
Судя по полученным оценкам, предприятия делятся на группы с многомерными средними ниже 100% (четыре предприятия), несколько выше 100% (два предприятия) и резко превышающие 100% (два предприятия). При большом объеме совокупности для выделения групп на основе многомерной средней необходимо установить интервалы значений многомерной средней;
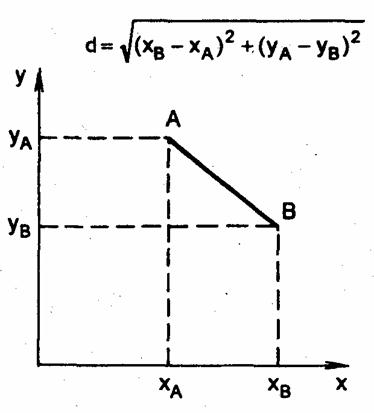
Затем следует провести группировку единиц: определить их количество в каждой группе и постараться указать, в чем состоят качественные различия между группами. Более обоснованным методом многомерной классификации является кластерный анализ. Само название метода происходит от того же корня, что и слово «класс», «классификация». Английское слово the cluster имеет значения: группа, пучок, куст, т. е. объединений каких-то однородных явлений. В данном контексте оно близко к математическому понятию «множества», причем, как и множество, кластер может содержать только одно явление, но не может в отличие от множества быть пустым. Каждая единица совокупности в кластерном анализе рассматривается как точка в заданном признаковом пространстве. Значение каждого из признаков у данной единицы служит ее координатой в этом «пространстве» по аналогии с координатами точки в нашем реальном трехмерном пространстве. Таким образом, признаковое пространство - это область варьирования всех признаков совокупности изучаемых явлений. Если мы уподобим это пространство обычному пространству, имеющему евклидову метрику, то тем самым мы получим возможность измерять «расстояния» между точками признакового пространства. Эти расстояния называют евклидовыми. Их вычисляют по тем же правилам, как и в обычной евклидовой геометрии. На плоскости, т.е. в двухмерном пространстве, расстояние между точками А и В равно корню квадратному из суммы квадратов разностей координат этих точек по оси абсцисс и по оси ординат - на основании теоремы Пифагора (рис. 6.1). Рис. 6.1. Евклидово расстояние В многомерном признаковом пространстве расстояние между точками р и q с k координатами, т. е. индивидуальными значениями k признаков, определяется так:
Совершенно очевидно, что нельзя суммировать квадраты отклонений одной точки от другой в абсолютных значениях разнокачествен-ных признаков. Необходимо сначала выразить различия между единицами совокупности по каждому признаку в каком-то относитель,но безразмерном показателе. В качестве такого показателя часто применяют «нормированную разность», т. е. величину:
По данным табл. 6.8 среднее квадратическое отклонение признака х, равно 109. Разделив все попарные разности значений этого признака на 109, получим матрицу нормированных разностей D1 (табл. 6.9). Очевидно эта матрица размером п×п симметрична. Таблица 6.9 Матрица нормированных разностей между предприятиями по среднемесячной оплате труда (D1)
Из данных табл. 6.9 видно, что величина нормированных разностей по этому признаку варьирует от 0 до 3,4. В нормально распределенной совокупности различия признака в среднем лишь в трех случаях из тысячи превосходят шесть сигм, т. е. в распределениях, близких к нормальным, величина нормированного расстояния редко превосходит 6. Средняя нормированная разность по данным табл. 6.9 составила 1,182. В нормально распределенной совокупности и совпадает со средним отклонением их от средней величины, т.е. нормированная разность в нормальной совокупности в среднем равна единице. Это очень важно при установлении предельного (критического) расстояния в признаковом пространстве, при достижении которого прекращается объединение кластеров. Аналогично вычисляются матрицы нормированных разностей по признакам х2, х3, х4 (см. табл. 6.10-6.12). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

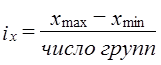


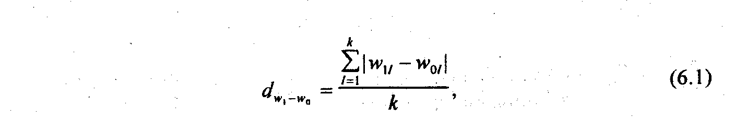
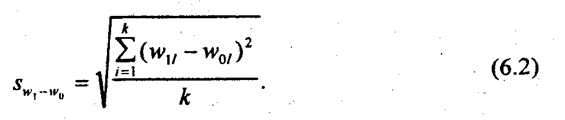
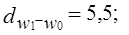
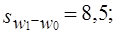 процентных пункта.
процентных пункта.