| Главная » Учебно-методические материалы » СТАТИСТИКА » Общая теория статистики: учебник. Под ред. Елисеевой И.И. |
| 23.01.2012, 13:39 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7.8. Статистическая проверка гипотез (общие понятия)Оценку генерального параметра получают на основе выборочного показателя с учетом ошибки репрезентативности. В другом случае в отношении свойств генеральной совокупности выдвигается некоторая гипотеза о величине средней, дисперсии, характере распределения, форме и тесноте бвязи между переменными. Проверка гипотезы осуществляется на основе выявления согласованности эмпирических данных с гипотетическими (теоретическими). Если расхождение между сравниваемыми величинами не выходит за пределы случайных ошибок, гипотезу принимают. При этом не делается никаких заключений о правильности самой гипотезы, речь идет лишь о согласованности сравниваемых данных. Основой проверки статистических гипотез являются данные случайных выборок. При этом безразлично, оцениваются ли гипотезы в отношении реальной или гипотетической генеральной совокупности. Последнее открывает путь применения этого метода за пределами собственно выборки: при анализе результатов эксперимента, данных сплошного наблюдения, но малой численности. В этом случае рекомендуется проверить, не вызвана ли установленная закономерность стечением случайных обстоятельств, насколько она характерна для того комплекса условий, в которых находится изучаемая совокупность. Особенно часто процедура проверки статистических гипотез применяется для оценки существенности расхождений сводных характеристик отдельных совокупностей (групп): средних, относительных величин. Такого рода задачи, как правило, возникают в социальной статистике. Трудоемкость статистико-социологических исследований приводит к тому, что почти все они строятся на несплошном учете. Поэтому проблема 'доказательности выводов в социальной статистике стоит особенно остро. Применяя процедуру проверки статистических гипотез, следует помнить, что она может гарантировать результаты с определенной вероятностью лишь по «беспристрастным» выборкам, на основе объективных данных. Статистической гипотезой называется предположение о свойстве генеральной совокупности, которое можно проверить, опираясь на данные выборки. Обозначается гипотеза буквой Н от латинского слова hypothesis. Так, может быть выдвинута гипотеза о том, что средняя в генеральной совокупности равна некоторой величине Н : μ = а, или о том, что генеральная средняя больше некоторой величины Н : μ > b. Различают простые и сложные гипотезы. Гипотеза называется простой, если она однозначно характеризует параметр распределения случайной величины. Например, Н : ц = а.'Сложная гипотеза состоит из конечного или бесконечного числа простых гипотез, при этом указывается некоторая область вероятных значений параметра. Например, Н : μ > b. Эта гипотеза состоит из множества простых гипотез Н :μ = с, где с — любое число, большее b. Гипотезы о параметрах генеральной совокупности называются параметрическими, о распределениях - непараметрическими. Гипотеза о том, что две совокупности, сравниваемые по одному или нескольким признакам, не отличаются, называется нулевой гипотезой (или нуль-гипотезой). Она обозначается Н0. При этом предполагается, что действительное различие сравниваемых величин равно нулю, а выявленное по данным отличие от нуля носит случайный характер. Например, Н0 : μ1 = μ2. Нулевая гипотеза отвергается тогда, когда по выборке получается результат, который при истинности выдвинутой нулевой гипотезы маловероятен. Границей невозможного или маловероятного обычно считают α = 0,05, т.е. 5%, или 0,01, 0,001. Если ориентироваться на правило «трех сигм», то вероятность ошибки α должна быть .равна 0,0027. Однако для этого уровня вероятности ошибки значения критериев редко табулируются: как правило, значения критериев в статистико-математических таблицах рассчитаны для вероятностей ошибки 0,05; 0,01; 0,001. Статистическим критерием называют определенное правило, устанавливающее условия, при которых проверяемую нулевую гипотезу следует либо отклонить, либо не отклонить. Критерий проверки статистической гипотезы определяет, противоречит ли выдвинутая гипотеза фактическим данным или нет. Проверка статистических гипотез складывается из следующих этапов: • формулируется в виде статистической гипотезы задача исследования; • выбирается статистическая характеристика гипотезы; • выбираются испытуемая и альтернативная гипотезы на основе анализа возможных ошибочных решений и их последствий; • определяются область допустимых значений, критическая область, а также критическое значение статистического критерия (t, F, χ2 ) по соответствующей таблице; • вычисляется фактическое значение статистического критерия; • проверяется испытуемая гипотеза на основе сравнения фактического и критического значений критерия, и в зависимости от результатов проверки гипотеза либо отклоняется, либо не отклоняется. При проверке гипотез по одному из критериев возможны два ошибочных решения: 1) неправильное отклонение нулевой гипотезы: ошибка 1-го рода; 2) неправильное принятие нулевой гипотезы: ошибка 2-го рода. В то время, как фактически нулевая гипотеза верна (1) и нулевая гипотеза не верна (2), принимают два ошибочных решения: 1) нулевая гипотеза отклоняется и принимается альтернативная гипотеза; 2) нулевая гипотеза не отклоняется. Возможные решения представлены в табл. 7.4. Таблица 7.4 Возможные выводы при проверке гипотез
Если, например, установлено, что новое минеральное удобрение лучше, хотя на самом деле его действие не отличается от старого, то это ошибка 1-го рода. Если мы решили, что оба вида удобрений одинаковы, то допущена ошибка 2-го рода. Вероятности, соответствующие неверным решениям, называются риском 1 и риском 2. Риск 1 равен вероятности ошибки а (уровню значимости), риск 2 равен вероятности ошибки р. Поскольку а всегда больше нуля, то всегда есть риск ошибки β. При заданных α и объеме выборки п значение β будет тем больше, чем меньше принятое α. Если п велико, то α и β могут быть сколь угодно малыми, т.е. решения будут более обоснованными. При малом объеме выборки и малом а возможность установить фактически существующие различия мала. Обычно задают значение а и пытаются сделать возможно β малым. Вероятность 1 - β называется мощностью критерия: чем она больше, тем меньше вероятность ошибки второго рода. Альтернативная гипотеза Н1 может быть сформулирована по-разному в зависимости от того, какие отклонения от гипотетической величины нас особенно беспокоят: положительные, отрицательные либо и те, и другие. Соответственно альтернативные гипотезы могут быть записаны как От того, как формулируется альтернативная гипотеза, зависят границы критической области и области допустимых значений. Критической областью называется область, попадание значения статистического критерия в которую приводит к отклонению Н0. Вероятность попадания значения критерия в эту область равна принятому уровню значимости. Область допустимых значений дополняет критическую область. Если значение критерия попадает в область допустимых значений, это свидетельствует о том, что выдвинутая гипотеза Нц не противоречит фактическим данным ( H0 не отклоняется). Точки, разделяющие критическую область и область допустимых значений, называются критическими точками или границами критической области. В зависимости от формулировки альтернативной гипотезы критическая область может быть двухсторонняя или односторонняя (левосторонняя либо правосторонняя). Если вычисляемое значение критерия попадает в критическую область, нулевая гипотеза отклоняется, она противоречит фактическим данным. 7.9. Проверка гипотезы о законе распределенияОдна из важнейших задач анализа вариационных рядов заключается в выявлении закономерности распределения и определении ее характера. Основной путь в выявлении закономерности распределения - построение вариационных рядов для достаточно больших со-вокупностей. Большое значение для выявления закономерностей распределения имеет правильное построение самого вариационного ряда: выбор числа групп и размера интервала варьирующего признака. Когда мы говорим о характере, типе закономерности распределения, то имеем в виду отражение в нем общих условий, определяющих вариацию. При этом речь всегда идет о распределениях качественно однородных явлений. Общие условия, определяющие тип закономерности распределения, познаются анализом сущности явления, тех его свойств, которые определяют вариацию изучаемого признака. Следовательно, должна быть выдвинута какая-то научная гипотеза, обосновывающая определенный тип теоретической кривой распределения. Под теоретической кривой распределения понимается графическое изображение ряда в виде непрерывной линии изменения частот в вариационном ряду, функционально связанного с изменением вариантов (значений признака). Теоретическое распределение может быть выражено аналитически - формулой, которая связывает частоты вариационного ряда и соответствующие значения признака. Такие алгебраические формулы носят название законов распределения. Большое познавательное значение имеет сопоставление фактических кривых распределения с теоретическими. Как уже отмечалось, часто пользуются типом распределения, которое называется нормальным. Формула функции плотности нормального распределения:
Следовательно, кривая нормального распределения может быть построена по двум параметрам - средней арифметической ц и среднему квадратическому отклонению ст. Гипотезы о распределениях заключаются в том, что выдвигается предположение о том, что распределение в генеральной совокупности подчиняется какому-то определенному закону. Проверка гипотезы состоит в том, чтобы на основании сравнения фактических (эмпирических) частот с предполагаемыми (теоретическими) частотами сделать вывод о соответствии фактического распределения гипотетическому распределению. Может проводиться и сравнение частостей. Под гипотетическим распределением необязательно понимается нормальное распределение. Может быть выдвинута гипотеза о биномиальном распределении, распределении Пуассона и т.д. Причина частого обращения к нормальному распределению в том, что в этом типе распределения выражается закономерность, возникающая при взаимодействии множества случайных причин, когда ни одна из них не имеет преобладающего влияния. Закон нормального распределения лежит в основе многих теорем математической статистики, применяемых для оценки репрезентативности выборок, при измерении связей и т. д. В социально-экономической статистике нормальное распределение встречается редко, но сравнение с ним важно для выяснения степени и характера отклонения от него фактического распределения. В главе 5 отмечалось, что близость средней арифметической величины, медианы и моды указывает на вероятное соответствие изучаемого распределения нормальному закону. Но более полная и точная проверка соответствия распределения гипотезе о нормальном законе производится с использованием специальных критериев, из которых рассмотрим наиболее употребимый критерий c2 (хи-квадрат) К. Пирсона. Для проверки гипотезы о соответствии эмпирического распределения закону нормального распределения необходимо частоты (частости) фактического распределения сравнить с частотами (частостями) нормального распределения. Значит, нужно по фактическим данным вычислить теоретические частоты кривой нормального распределения f̂ по формуле (для дискретных рядов): где п - объем выборки; i - величина интервала вариационного ряда. Значение ординат кривой нормального распределения f(t) можно получить по таблицам значения функции: Проверяемая гипотеза формулируется как Н0: fj = f̂j альтернаивная - как Н1: fj ≠ f̂j. Проверка гипотезы требует, чтобы был построен теоретический ряд распределения с частотами f̂j, соответствующими нормальному закону, при тех же значениях параметров распределения Методика построения теоретического ряда такова: 1. По фактическому интервальному ряду (табл. 5.6) вычисляются значения / для каждой группь< хозяйств по формуле (для интервальных рядов):
2. Вычисляется вероятность попадания единицы наблюдения в данный интервал при выполнении гипотезы о нормальном законе: где |tj| > |tj+1| 3. Определяется теоретическая частота в данной группе, равная произведению объема совокупности на вероятность попадания в данный интервал: 4. Находится значение критерия c2 по формуле где k — число категорий ряда распределения; j - номер категории; fj - частота эмпирического распределения; f̂j - частота теоретического распределения. При расчете c2 частоты можно заменить частостями: где pj - частости эмпирического распределения; pj - вероятности теоретического распределения. При этом, согласно Ф. Йейтсу (Jates), группы с теоретическими частотами менее 5 принято объединять, что снижает влияние случайных ошибок (см. [6]). Если все эмпирические частоты равны соответствующим теоретическим частотам, то c2 равно нулю. Очевидно, что чем больше отличаются эмпирические и теоретические частоты, тем c2 больше; если расхождение несущественно, то c2 должно быть малым. Имеются специальные таблицы критических значений c2 при 5%-ном и 1%-ном уровнях значимости. Критические значения зависят от числа степеней свободы (d.f. - degrees of freedom) и уровня значимости. Число степеней свободы рассчитывается так: если эмпирический ряд распределения имеет k категорий, то k эмпирических частот f1, f2, …, fk должны быть связаны следующим соотношением: d.f. = (k - 1) - р = k - (р + 1). (7.30) Полученное значение критерия c2 сравнивается с табличным при числе степеней свободы, равном числу групп (с условием Ф. Йейтса), за минусом трех - по числу фиксированных параметров в формуле нормального закона распределения и с учетом равенства сумм теоретических и фактических частот (см. приложение, табл. 4). В первой графе этой таблицы дано число степеней свободы, а в заголовках граф - уровни значимости. Если фактическое значение c2 превышает табличное при том же числе степеней свободы, то вероятность соответствия распределения нормальному закону меньше указанной. Результаты расчета c2 по данным табл. 5.6 (глава 5) приведены в табл. 7.5 при х = 30,3; s = 8,44. Сумма теоретических частот нормального распределения меньше суммы фактических частот, так как нормальный закон не ограничен рамками фактических минимума и максимума. Число групп после объединения малочисленных составило 7. Критическое значение c2 по табл. 4 приложения при 7-3 = 4 степеням свободы и значимости 0,05 составляет 9,49. Значит, вероятность расхождения распределения с нормальным меньше 0,05, и вероятность соответствия его нормальному закону больше 0,95. Табличное значение c2 для значимости 0,1 равно 7,78, что также больше фактического. Таблица 7.5 Проверка соответствия распределения хозяйств по урожайности зерновых культур нормальному закону
Ясно, что гипотеза о соответствии распределения хозяйств по урожайности нормальному закону не может быть отклонена. Какое практическое значение может иметь произведенная проверка гипотезы? Во-первых, соответствие нормальному закону позволяет прогнозировать, какое число хозяйств (или доля совокупности) попадает в тот или иной интервал значений признака. Во-вторых, нормальное распределение возникает при действии на вариацию изучаемого показателя множества независимых факторов. Из этого следует, что нельзя существенно снизить вариацию урожайности, воздействуя только на один-два управляемых фактора, скажем удобрения или энергозатраты. С помощью критерия c2 можно проверять не только гипотезу о согласии эмпирического распределения с нормальным законом, но и с любым другим известным законом распределения - равномерным распределением, распределением Пуассона и т. д. Например, суд рассматривает жалобу посетителей казино на то, что, по их мнению, игральная кость, которой там пользуются, фальшива, некоторые числа очков, якобы, выпадают чаще, чем другие, и этим пользуются крупье, обирающие игроков. Суд назначает экспертизу игральной кости: эксперт делает 600 бросков и записывает число выпавших единиц, двоек, троек и т. д. Полученное эмпирическое распределение сравнивается с теоретическим, т. е. равномерным: в правильной кости вероятность выпадения каждого числа очков должна быть равна 1/6, при 600 бросках это даст по 100 выпадений каждого числа очков. С помощью критерия c2 проверяется нулевая гипотеза о том, что различия эмпирического и теоретического распределений случайны, т. е. не являются систематическим результатом фальсификации формы кости или положения центра тяжести в ней; H0 : fфакт = fтеор. Результаты испытания и расчет у приводятся в табл. 7.6. Таблица 7.6 Результаты испытания игральной кости
Табличное значение c2 при уровне значимости 0,05 (это вероятность ошибочного отклонения нулевой гипотезы при условии, что она верна) и при 6-2=4 степенях свободы (фиксировано 2 параметра: сумма числа бросков 600 и вероятность каждого числа очков - 1/6) составляет 9,49. Вычисленное значение c2 =5,8, что значительно ниже табличного. Следовательно, нулевая гипотеза не отклоняется: распределение бросков по числу выпавших очков нельзя считать неравномерным. Обвинение игроков против служащих казино не подтверждено достаточно надежно, но не доказано и то, что кость правильная. Можно назначить более дорогую экспертизу - сделать 100 000 бросков кости, но можно и согласиться, что вероятность ошибочного признания правильности кости мала - всего 5% - и отклонить обвинение. Выбор закона распределения проводится на основе теоретического анализа. Кроме того, целесообразно руководствоваться следующей рекомендацией: выражение, определяющее функцию плотности распределения, должно зависеть от возможно меньшего числа параметров. Например, экспоненциальное распределение зависит от одного параметра - средней величины; нормальное и логнормальное распределение - от двух параметров. 7.10. Проверка гипотезы о связи на на основе критерия c2 (хи-квадрат)Одним из основных приложений критерия c2 является его использование при анализе таблиц сопряженности двух переменных для установления факта наличия и уровня значимости взаимосвязи. Как правило, критерий у2 применяется для анализа таблиц сопряженности номинальных признаков, однако" он может быть использован и при анализе взаимосвязи порядковых или интервальных (количественных) переменных, несмотря на то, что для последних . случаев существуют более мощные тесты. Рассмотрим общий случай - таблицу сопряженности двух переменных размером r ´ s. Обозначим: nij - наблюдаемая частота (число объектов) в ячейке (ij) таблицы, так называемая фактическая клеточная частота; n̂ij - теоретически ожидаемая (по Н0) частота в этой ячейке, i = 1, 2, ..., r, j = 1, 2, ..., s; r - число строк, s - число столбцов.
В этом случае испытуемая гипотеза Н0: nij ≠ n̂ij или Н0 : c2 =0, альтернативная гипотеза H1: nij ≠ n̂ij . Критерий c2 для проверки Н0 имеет вид: Расчет теоретически ожидаемых частот в ячейках таблицы сопряженности должен производиться, как мы уже указывали выше, в предположении справедливости нулевой гипотезы. Нуль-гипотеза (Н0) в данном случае есть предположение о статистической независимости рассматриваемых переменных. Как известно из теории вероятностей, две случайные величины (события) являются статистически независимыми, если вероятность их совместной реализации равна произведению вероятностей реализации каждой из них по отдельности, т. е. где В нашем случае выборочными оценками соответствующих вероятностей p будут являться величины р(хi, хj) = пij/п, и поэтому расчет теоретически ожидаемой по Н0 частоты п̂ij следует производить по формуле т. е. произведение итогов по столбцу и строке, деленное на общий объем данных. Если подставить выражение п̂ij в формулу (7.32), то получим Используя эту формулу, мы можем находить эмпирические значения критерия c2 без промежуточного вычисления теоретических частот в явном виде. Очевидно, что для определения эмпирического значения критерия c2 нет необходимости рассчитывать все s теоретических частот в каждой строке, а достаточно найти лишь s - 1 значение частоты в r - 1 строке, так как оставшиеся частоты могут быть получены как разности между маргинальными суммами эмпирических частот и суммами известных теоретических частот, т. е. значения теоретических частот в последних строке и столбце таблицы всегда полностью детерминированы. Поэтому число степеней свободы для r ´ s таблицы сопряженности равно: d.f.= (r - 1) (s -1). (7.35) Заметим, что для таблицы 2´2 число степеней свободы равно 1. В таблице распределения статистики c2d.f.a приведены значения этой величины для различных уровней значимости при различных числах степеней свободы (см. приложение, табл. 4). Например, на уровне a = 0,01 для d.f. = 1 мы находим c2 = 10,827. Это означает, что равное или большее значение этой величины c2 может встретиться только один раз из тысячи при условии, что все сделанные допущения (нуль-гипотеза) справедливы. Другими словами, если выполняется предложение об отсутствии взаимосвязи между переменными, то крайне маловероятно (Р < 0,001), что наблюдаемые и ожидаемые частоты будут отличаться настолько, что фактическая величина c2 будет равной или большей 10,827. Если же c2ф ³ c2d.f.a, то гипотеза Н0 на данном уровне значимости а может быть отвергнута. Вероятность того, что, отвергая нулевую гипотезу, мы совершаем ошибку (первого рода), которая численно равна уровню значимости о., задаваемому при проверке гипотезы. Интерпретация c2 теста зачастую усложняется, когда в таблице сопряженности имеются ячейки с нулевыми значениями наблюдаемых частот. Дело в том, что если пара (хi, хj) значений переменных не наблюдалась в выборке, то это может означать, что объем выборки не столь велик, чтобы зафиксировать такую редкую комбинацию, либо что данная комбинация невозможна по каким-то объективным причинам. В последнем случае действительное число степеней свободы анализируемой системы меньше числа степеней свободы таблицы сопряженности, на основании которого произведена оценка уровня значимости c2 теста. Корректировка применения c2 теста возможна лишь в том случае, если эмпирические данные, наполняющие таблицу сопряженности, есть результаты независимой случайной выборки относительно большого объема п. Последнее требование вызвано тем, что выборочное распределение c2 аппроксимирует табличное распределение статистики c2 только при больших п. Естественно, возникает вопрос о том, насколько велико должно быть п, чтобы иметь возможность использовать данный тест. Ответ на этот вопрос зависит от числа ячеек и величин маргинальных сумм. Вообще говоря, чем меньше число ячеек и чем более близки между собой по величине маргиналы, тем меньше может быть п. Существует, однако, практическое число, позволяющее оценить снизу по п диапазон возможного применения критерия c2 : если в данной таблице сопряженности любая из теоретических ожидаемых частот п̂ij в ячейке (i, j) не больше 5, то рекомендуется произвести, если это возможно, модификацию таблицы либо воспользоваться другим критерием. В общем случае корректировка таблицы размера r ´ s затруднительна. Практика показала, что если число ячеек велико, а ожидаемые частоты, равные или меньше пяти, встречаются лишь в одной-двух ячейках, то проведение корректировки нецелесообразно; во всех иных случаях разумной альтернативой является объединение категорий (градаций) с тем, чтобы элиминировать подобные ячейки. Естественно, такое объединение должно быть таким, чтобы получаемая в результате комбинация не была содержательно бессмысленной. Пример. Согласно опросу 157 предпринимателей, работающих в приватизированных кафе и ресторанах, относительно оценки возможностей деятельности при разных формах собственности получены следующие данные (табл. 7.7). Таблица 7.7 Исходные данные
Испытаем гипотезу о независимости переменных Н0 : пij = n̂ij, где пij - генеральные частоты, оценками которых выступают выборочные частоты пij. Теоретические частоты, рассчитанные в соответствии с нуль-гипотезой как Таблица 7.8 Теоретические частоты
Таким было бы распределение ответов о возможностях деятельности, если бы формы собственности никак не сказывались. Задавая уровень значимости a = 0,05, наводим по табл. 4 приложения критическое значение критерия c22 a, df при числе степеней свободы d.f. = (3 - 1)(5-1) = 8. Отсюда c22 a, df = 15,51. Различия между фактическими и теоретическими клеточными частностями обобщаются в величине c2:
Так как c2факт > c2крит, Н0 отклоняется, т.е. форма собственности небезразлична для деятельности кафе и ресторанов. Таким образом, наблюдаемое значение c2 является значимым на 5%-ном уровне значимости, и нулевая гипотеза может быть отвергнута в пользу альтернативной. Итак, мы рассмотрели один из возможных способов ответа на вопрос: существует ли связь между двумя переменными? Для этого мы выдвинули нулевую гипотезу, что такой связи нет, а затем рассмотрели способ статистического испытания этой гипотезы. Мы можем оценить величину риска в принятии предположения о существовании связи. Но означает ли это, что данная связь существенна с точки зрения ее силы? Вовсе не обязательно. Вопрос о силе или степени, тесноте зависимости — это иной вопрос, отличный от вопроса о существовании взаимосвязи. В социально-экономических исследованиях, как правило, установление факта наличия связи между переменными не самоцель. Установив наличие связи, исследователь должен измерить ее силу (тесноту) с тем, чтобы иметь возможность сравнивать взаимосвязи между различными характеристиками, выделять наиболее сильные из них (см. гл. 8). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

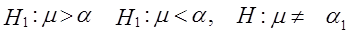 .
.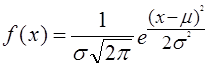 .
.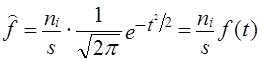 , (7.27)
, (7.27)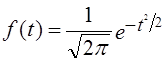 .
.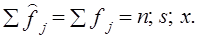
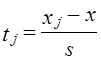 -для начала и конца интервала.
-для начала и конца интервала.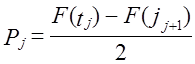 ,
,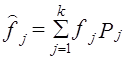
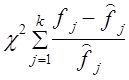 (7.28)
(7.28)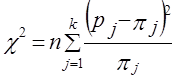 (7.29)
(7.29)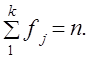 Если параметры теоретического распределения известны, то только k - 1 частот могут принимать произвольные значения, т. е. свободно варьировать, а последняя частота может быть найдена из указанного соотношения. Поэтому говорят, что система из k частот благодаря наличию одной связи теряет одну «степень свободы» и имеет только k — 1 степеней свободы. Кроме того, если при нахождении теоретических частот р параметров теоретического распределения неизвестны, то они должны быть найдены по данным эмпирического ряда. Это накладывает на эмпирические частоты еще р связей, благодаря чему система теряет еще р степеней свободы. Таким образом, число свободно варьируемых частот (а значит, и число степеней свободы) становится равным:
Если параметры теоретического распределения известны, то только k - 1 частот могут принимать произвольные значения, т. е. свободно варьировать, а последняя частота может быть найдена из указанного соотношения. Поэтому говорят, что система из k частот благодаря наличию одной связи теряет одну «степень свободы» и имеет только k — 1 степеней свободы. Кроме того, если при нахождении теоретических частот р параметров теоретического распределения неизвестны, то они должны быть найдены по данным эмпирического ряда. Это накладывает на эмпирические частоты еще р связей, благодаря чему система теряет еще р степеней свободы. Таким образом, число свободно варьируемых частот (а значит, и число степеней свободы) становится равным: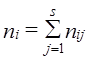 - сумма по j-й строке маргинальные частоты
- сумма по j-й строке маргинальные частоты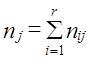 - сумма по j-у столбцу (7.31)
- сумма по j-у столбцу (7.31)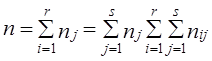 - общее число объектов или объем выборки.
- общее число объектов или объем выборки.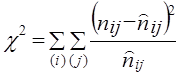 . (7.32)
. (7.32)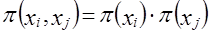 ,
,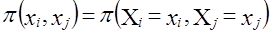
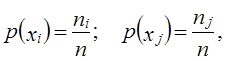
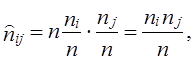 (7.33)
(7.33)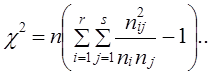 (7.34)
(7.34)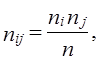 представлены в табл. 7.8.
представлены в табл. 7.8.