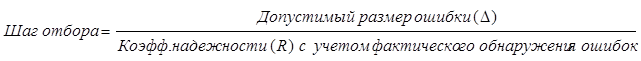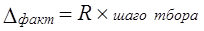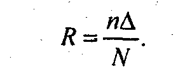| Главная » Учебно-методические материалы » СТАТИСТИКА » Общая теория статистики: учебник. Под ред. Елисеевой И.И. |
| 23.01.2012, 13:39 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7.11. Проверка гипотезы о средних величинахОсновные гипотезы о средних величинах следующие: гипотезы о значении генеральной средней (при известной генеральной дисперсии или при неизвестной генеральной дисперсии); гипотезы о равенстве генеральных средних нормально распределенных сово-купностей (при известных генеральных дисперсиях, при неизвестных равных генеральных дисперсиях, при неизвестных неравных генеральных дисперсиях). Первая задача чаще всего решается при неизвестной генеральной дисперсии. Испытуемая гипотеза Н0 : m = m0, альтернативная гипотеза Н1: m ≠ m0. Испытание гипотезы проводят с помощью t- критерия. При большом числе наблюдений критическое значение критерия определяется по таблице интеграла вероятностей, при малом - по таблице распределения Стьюдента с заданным уровнем значимости и числом степеней свободы, п — 1. Если испытуемая гипотеза Н0: m = а, то фактическое значение критерия представляет отношение оцениваемой разности к средней возможной ошибке выборочной средней. где Если tфакт > tкрит , Н0 не отклоняется, если tфакт < tкрит , H0 отклоняется. Рассмотрим пример.Часовая выработка забойщика при добыче угля в шахте по норме составляет 400 кг. Фактическая выработка соответствовала норме. При переходе в новый забой условия работы забойщиков усложнились. Для проверки обоснованности нормы в новых условиях был проведен учет работы 9 забойщиков: их средняя часовая выработка составила 388 кг с дисперсией, равной s2 = 171. Выдвигается гипотеза о том, что норму выработки пересматривать не нужно, т.е. Н0 : m = 400 кг. Проверим эту гипотезу на 5%-нюм уровне значимости. Критическое значение t-критерия определяется по таблице распределения Стьюдента при доверительной вероятности 0,95 (1 - 0,05) и числе степеней свободы d.f. =- n - 1 = 8. Критическое значение составит tкрит = 2,3. Фактические значения t-критерия вычисляются по формуле (7.36): Поскольку tфакт > tкрит Н0 отклоняется. Норма выработки в новых условиях должна быть пересмотрена, так как производительность труда стала существенно ниже нормативной. В рассмотренном примере различие между фактическим и таб-~ личным значениями /-критерия невелико, поэтому вывод недостаточно надежен. Надежность вывода вообще понижается, если нет уверенности в нормальном распределении генеральной совокупности. Гипотеза о равенстве средних может рассматриваться как гипотеза о связи, если сопоставляются средние величины, обусловленные действием какого-либо фактора. Например, сравнивается средняя заработная плата рабочих двух специальностей. Нулевая гипотеза состоит в том, что специальность рабочего не влияет на заработок. Если окажется, что tфакт > tкрит, нулевую гипотезу отклоняют и делают вывод о том, что специальность оказывает влияние на заработную плату. Рассмотрим решение этой задачи при условии, что генеральные дисперсии неизвестны, но принимаются равными. При сравнении средних величин выдвигается гипотеза, что обе выборки принадлежат одной и той же генеральной совокупности со средней m и дисперсией s2. При неизвестной генеральной дисперсии формула t-критерия имеет вид:
Поскольку s21 и s22 рассматриваются как выборочные оценки общей дисперсии s2, то формула (7.37) может быть записана так:
где x̅1, x̅2 - выборочные средние; s2 - выборочная оценка общей дисперсии; Гипотеза H0 отклоняется, если Рассмотрим пример. Для проверки устойчивости цен на яблоки в летний период на двух рынках города проведено выборочное обследование: на первом рынке по данным 15 продавцов определена средняя цена, равная 2 тыс. руб./кг. при среднем квадратическом отклонении s2 = 0,5 тыс. руб.; на втором рынке обследовано 17 продавцов, средняя цена оказалась равной 2,5 тыс. руб./кг, s2 = 0,4 тыс. руб. Н0 : m = m0, Н1: m ≠ m0. При a = 0,05 и d.f. = 30, tкрит = 2,042, tфакт > tкрит , H0 отклоняется, т. е. различия в ценах на двух рынках нельзя объяснить лишь случайностями выборки. Проверка той же нулевой гипотезы при односторонней критической области будет проводиться на следующих условиях определения: tкрит : 1 - 2a и d.f. = n1 + n2 -2. Следовательно, если Н1 : m1 = m2 (2a = 0,1, d.f. = 30), так что H0 опять-таки отклоняется. Случай проверки гипотезы о средних величинах при неизвестных дисперсиях, равенство которых не предполагается, здесь не рассматривается ввиду его недостаточной теоретической разработанности. 7.12. Основы дисперсионного анализаМожет быть поставлена задача сравнения двух выборочных дисперсий. Для ее решения применяется критерий, названный в честь английского статистика Рональда Фишера (1890 - 1968) F- критерием. Этот критерий представляет собой отношение выборочных дисперсий s21 и s22, которые рассматриваются как оценки одной и той же генеральной дисперсии s2: Испытуемая гипотеза является нулевой гипотезой Н0 : s21 = s22 = s2, альтернативная гипотеза Н1 : s21 ≠ s22 ≠ s2 . F-критерий строится так, что в числителе стоит бо́льшая дисперсия. Fmin = 1, Fmax ® ¥ . Критические значения критерия F берутся из таблиц F-распределения. F-распределение зависит от уровня значимости и от числа степеней свободы сравниваемых дисперсий d.f.1 и d.f.2 (cм. приложение, табл. 3). В дисперсионном анализе общая вариация подразделяется на составляющие и производится сравнение этих составляющих. Испытуемая гипотеза состоит в том, что если данные каждой группы представляют случайную выборку из нормально распределенной генеральной совокупности, то величины всех частных дисперсий должны быть пропорциональны своим степеням свободы и каждую из них можно рассматривать как оценку генеральной дисперсии. Дисперсионный анализ часто применяется совместно с аналитической группировкой (см. гл. 6). В этом случае данные подразделяются на группы по значениям признака-фактора, вычисляются значения средних величин результативного признака в группах, считается, что различия в их значениях определяются различиями в значениях фактора. Задача состоит в оценке существенности различий между средними значениями результативного признака в группах. Итак, испытуемая гипотеза может быть записана как гипотеза о средних величинах Н0 : m1 = m2 =m3 =… Как было показано в предыдущем параграфе, когда выделяются две группы, эта задача решается с помощью t-критерия. Если же число сравниваемых групп больше двух, то существенность различий между группами доказывается с помощью дисперсионного анализа, на основе F-критерия. Заметим, что результаты дисперсионного анализа, так же как и выводы о характере связи, значения показателей ее силы и тесноты, зависят от числа групп, выделенных по признаку-фактору. В случае выделения групп по одному фактору мы имеем так называемый однофакторный дисперсионный комплекс. Разложение дисперсии при этом производится в соответствии с правилом сложения дисперсий (см. гл. б): где уij - значение результативного признака у i-й единицы в j-й группе; i - номер единицы, i = 1, .... п.; j - номер группы; пj- численность у-й группы; yj - средняя величина результативного признака в у-й группе; у̅ — общая средняя результативного признака. Если обозначить суммы квадратов отклонений буквой D, получим равенство: Dобщ = Dфакт +Dост (7.41) На основе разложения дисперсии (7.41) в соответствии с гипотезой отсутствия различий между группами могут быть получены три оценки генеральной дисперсии, пропорциональные степени свободы: на основе общей вариации, межгрупповой (факторной) и внутригрупповой (остаточной). Число степеней'свободы равно: для общей вариации для межгрупповой вариации для внутригрупповой вариации Как и суммы квадратов отклонений, числа степеней свободы связаны между собой равенством: или п - 1 = (m - 1) + (п - т). (7.42) Деление сумм квадратов отклонений на соответствующее число степеней свободы дает три оценки генеральной дисперсии s2 .
Поскольку Dфакт измеряет вариацию результативного признака, связанную с изменением фактора, по которому произведена группировка, a Dост - вариацию, связанную с изменением всех прочих факторов, сравнение этих величин, рассчитанных на одну степень свободы, дает возможность оценить существенность влияния признака-фактора на результативный признак с помощью F-критерия: Эта запись предполагает, что s2факт > s2ост. Как правило, мы получаем именно такое соотношение. Если F факт > Fтабл (a., d.f.1, d.f.2), можно утверждать, что нуль-гипотеза не соответствует фактическим данным, влияние признака-фактора является существенным или, иначе говоря, статистически значимым. Рассмотренные этапы однофакторного дисперсионного анализа представлены в табл. 7.9. Таблица 7.9 Схема однофакторного дисперсионного анализа
По данным табл. 6.6 проверим гипотезу Н0 : m 1= m2 ..., т. е. предположим, что оборачиваемость средств никак не влияет на прибыль. Dфакт = 172,76, d.f.факт =3-1=2, s21 = 86,38; Dост – Dобщ - Dфакт = 224,4 - 172.76 = 51,64; d.f.ост = 20 - 3=17; s22 = 3,03. Тогда F = 28,5. Критическое значение F-критерия из табл. 3 приложения F(a=0,05, d.f.1=2, d.f.2=17) = 3,59. Таким образом Fфакт > Fкрит следовательно, Н0 отклоняется. Действительно, скорость оборота средств является очень важным фактором формирования прибыли, на это указывало и значение эмпирического корреляционного отношения h = 0,881. Рассмотрим двухфакторный дисперсионный анализ, основой проведения которого служит комбинационная группировка по двум факторам х и z, с последующим разложением дисперсии результативного признака у:
где i - номер единицы в j-й группе по признаку х и k-й по признаку z; j = 1̅,т̅, k =I̅р̅, у̅jk - среднее значение признака у̅ в группе, образованной ком-бинацией j-го значения признака х и k-го значения признака z; у̅j - среднее значение признака у в j-й группе по признаку х; y̅k - среднее значение признака у в k-й группе по признаку z; у̅ - общая средняя признака y в целом по выборке; пjk - число единиц в группе, образованной комбинацией j-го значения признака х и k-го значения признака z; пj - число единиц в j-й группе по признаку х, пk - число единиц в k-й группе по признаку z; т Р т р п- общее число единиц, Равенство (7.44) можно записать так: Dобщ = Dx + Dz + Dxz + Dост (7.45) где Dч - вариация у под влиянием фактора x; Dz - вариация у под влиянием фактора z; Dxz - вариация у, обусловленная взаимодействием факторов х и z; Dост - вариация у под влиянием прочих факторов. Первые три слагаемые составляют вариацию признака у, вызванную изучаемыми факторами, поэтому равенство (7.45) можно записать в виде: Dобщ = Dфакт +Dост (7.46) где Dфакт = Dх + Dz + Dxz. (7.47) Величина Dфакт может быть рассчитана не через составляющие, а непосредственно как Однако при неравенстве численностей подгрупп пjk и групп пj и пk равенство нарушается (за счет взвешивания при неравных весах). Поэтому рассчитываются невзвешенные величины:
Затем на основе сравнения взвешенной (7.48) и невзвешенной величин факторной дисперсии находят поправочный коэффициент:
Этот коэффициент используется для корректировки невзвешенных сумм квадратов отклонений Число степеней свободы для каждой суммы квадратов отклонений составляет: d.f.x=m- 1; d.f.z = p - 1; d.f.xz = (m-1)(p -1) = mp - т - р + 1, в целом d.f.факт = d.f.x + d.f.z + d.f.xz = mp-1;
В двухфакторном дисперсионном анализе испытуемые гипотезы формулируются следующим образом: 1. Н0 : m1∙ = m2. =…mm 2. Н0 : m1∙ = m2. =…mp 3. Н0 : m1∙ = m2. =…mmp Вся процедура двухфакторного дисперсионного анализа обобщается в табл. 7.10. Таблица 7.10 Схема двухфакторного дисперсионного анализа
Решение о первой гипотезе принимается на основе сравнения
Если Fфакт > Fкрит, то Н0 отклоняется. Вторая гипотеза испытывается на основе сравнения
Третья - на основе сравнения
Во всех случаях, если Fфакт > Fкрит, Н0 отклоняется. На основе F-критерия принимаются решения о форме уравнения регрессии, о статистической значимости той или иной объясняющей переменной при построении многофакторного уравнения регрессии (см. гл. 8) и др. Рассмотренные направления проверки статистических гипотез охватывают лишь важнейшие из них. Процедура испытания статистических гипотез применяется для определения того, случайно или нет полученное значение коэффициента корреляции, коэффициента вариации и т. д., случайны или нет различия в значениях показателей (медиан, коэффициентов корреляции, регрессии и т.д.) в разных совокупностях. Во всех случаях результатом является вероятностное суждение, которое составляет сущность анализа данных в разнообразных сферах: в медицине, биологии, технике, политике, спорте, экономике, психологии и социологии. 7.13. Примеры применения выборочного метода и проверки статистических гипотезПотребность в использовании выборочного метода, выработке вероятностных суждений в современной отечественной практике непрерывно расширяется. В государственной статистике основными направлениями использования выборочного метода традиционно являются бюджетные обследования семей, выборочные переписи населения, контрольные обходы и проверки после проведения сплошных обследований. Создание единого государственного регистра предприятий и организаций (ЕГРПО), в котором фиксируются все хозяйствующие субъекты на территории Российской Федерации всех форм собственности, открывает возможность проведения разнообразных выборочных обследований в области экономики. В области социальных исследований для государственной статистики главным является бюджетное обследование, которое охватывает примерно 48 тыс. домохозяйств. Оно основано на многоступенчатом отборе. Общий объем выборки распределяется по сферам занятости (для работающих) и территориям. Затем для работающих производится отбор предприятий в пределах каждой отрасли в отобранной территории. Если, например, нужно отобрать 100 рабочих, занятых в определенной отрасли, для обследования семейных бюджетов так, чтобы на каждом отобранном предприятии было не менее 20 бюджетов, включающих рабочих с разным уровнем заработной платы, то, значит, должно быть отобрано 100 :20 =5 предприятий. Отбор предприятий проводят по списку, в котором предприятия располагаются в порядке убывания средней заработной платы рабочих, указываются общее число рабочих, их суммарная заработная плата. Шаг отбора определяется делением общего числа рабочих на предприятиях данной отрасли на- число отбираемых предприятий. Если всего на предприятиях данной отрасли в области занято 30525 человек, то шаг отбора равен 30 525 : 5 = 6105. По данным кумулятивной численности рабочих с данным шагом отбора производится отбор предприятий, которые затем проверяются на репрезентативность по показателю средней месячной заработной платы. Следующая стадия связана с отбором рабочих на выбранных предприятиях: среди 20 бюджетов должны быть пропорционально представлены бюджеты семей малоквалифицированных и высококвалифицированных рабочих, а среди этих категорий отбор проводится механически по спискам рабочих, составленным в порядке убывания среднемесячной заработной платы. Выборочная совокупность при бюджетных обследованиях включает и семьи неработающих (пенсионеров, студентов, инвалидов) и одиночек. Задачей статистики в области бюджетных обследований является обеспечение представительства всех социальных групп и учет всех источников дохода. Наиболее общим показателем уровня благосостояния населения являются денежные доходы, поступающие в семью в виде заработной платы, премий, единовременных выплат, гонораров, предпринимательского дохода или дохода от собственности, компенсационных выплат и дотаций. В совокупные доходы семьи включаются также натуральная оплата труда, доходы, полученные от реализации и потребления продукции личного подсобного хозяйства (садового участка, коллективного огорода). Для характеристики обеспеченности семей следует учитывать их накопления, а также валютные поступления. Возрастает значение анализа личного потребления. Большое значение имеет применение выборочного метода на промышленных предприятиях для статистического контроля качества продукции и использования внутрисменного времени рабочих. Контроль качества продукции проводится для готовой продукции и в процессе ее изготовления. Выборочный контроль качества готовой продукции осуществляется так: отбирается на пробу некоторое число изделий и оценивается качество каждого из них. По доле дефектных изделий среди отобранных судят о качестве всей партии изделий. Если доля брака не превышает некоторого допустимого предела, то вся партия принимается без сплошного контроля. Если же доля брака больше допустимого предела, то проводится сплошная проверка всех остальных изделий в партии, конечно, если она не связана с уничтожением или порчей изделий. При проведении контроля на стадии производства продукции машиностроения металлообработки основное внимание уделяется контролю положения центра настройки станков и вариации размеров деталей, обработанных на металлорежущем оборудовании. Для изучения структуры рабочего времени разных категорий работников, особенно рабочих, а также для характеристики использования машин и оборудования используется метод моментных наблюдений. Этот метод состоит в регистрации вида затрат времени в определенные, заранее выбранные моменты. Заранее составляется список всех возможных состояний или видов затрат времени. Подсчитывается доля отметок о каждом состоянии, и оценивается доверительный интервал доли времени, затраченного на тот или иной вид работы. Отбор моментов выборки может быть проведен либо по схеме механической выборки — через равные промежутки времени, либо по схеме случайной выборки с использованием таблицы случайных чисел. Необходимая численность моментов наблюдения рассчитывается как Если принять доверительную вероятность равной 0,954 и допустимую ошибку 0,005, т.е. 0,5%, то При продолжительности наблюдений 10 дней и охвате наблюдением 100 рабочих, в день должно проводиться 40 наблюдений за каждым рабочим. Если продолжительность смены составляет 8 ч, то интервал между обходами должен составлять 12 мин. [(8 ч ∙ 60 мин.) : 40 наблюдений]. За начальный момент времени можно принять момент начала смены плюс пол-интервала: 7 ч 30 мин. + 6 мин. =7 ч 36 мин., тогда второй обход будет проводиться в 7 ч 48 мин. и т.д. По итогам моментного наблюдения рассчитываются доверительные интервалы для каждого i-го вида потерь рабочего времени:
Результаты наблюдений используются для анализа потерь рабочего времени, статистической оценки напряженности труда рабочих. Выборочный метод используется в аудиторской практике при проверке бухгалтерских документов. При этом решаются две задачи: 1) дать оценку количества документов в данной фирме (предприятии, объединении, и т. д.), в оформлении которых не соблюдались принятые правила; 2) оценить правильность указанных в документах сумм денежных средств. Первую задачу решают с помощью так называемой атрибутивной выборки, вторую - с помощью монетарной выборки. В первой выборке единицей отбора является учетный документ, во второй - денежная единица. При организации атрибутивной выборки в качестве генеральной совокупности выступает вся совокупность расчетных документов фирмы за проверяемый период. Обычно она предварительно разбивается на однородные массивы: по характеру документов, по центрам ответственности, по географическому признаку, по временной последовательности, по интенсивности запросов на данный вид информации и т.д. Каждому документу присваивается числовая метка, и по таблице случайных чисел проводится отбор номеров в количестве, соответствующем объему выборки. Можно провести и механический отбор с шагом отбора, равным N : п , где N - объем генеральной совокупности, п - объем выборки. Обычно начинают отбор не с первого документа, а отступив полшага. Объем атрибутивной выборки находится из соотношения:
Коэффициент надежности определяется по таблице распределения Пуассона, поскольку появление ошибки в оформлении расчетных документов относится к классу редких событий. При этом предполагаемая средняя частота ошибок закрепляется на определенном уровне, например 1; 1,5 или 2. Если фактическая частота несоответствий в оформлении документов меньше максимально допустимой, то вычисляют коэффициент надежности как произведение объема выборки на величину фактической частоты несоответствий, после чего по таблице распределения Пуассона определяют вероятность, соответствующую рассчитанной величине коэффициента надежности, чтобы убедиться, что доверительная вероятность результатов выборки достаточно высока. Если фактически выявленная частота несоответствия принятым - правилам превышает максимально допустимую величину, то обязательно проводят монетарную выборку. При монетарной выборке генеральной совокупностью является сумма денежных средств, зафиксированных во всех проверяемых документах. В качестве единицы отбора выступает денежная единица (1 руб.), а единицей наблюдения является расчетный документ. Требуемая точность результатов задается как допустимая относительная сумма ошибки. Объем монетарной выборки рассчитывается как
Например, если аудитор исходит из 1%-ного риска (при односторонней критической области — опасения, что суммарная ошибка будет не больше принятой величины), т. е. при 98%-ной доверительной вероятности наличия суммарной ошибки 50 000 руб. при объеме генеральной совокупности, равном 60 млн/ руб., то объем выборки
Определяется шаг отбора, равный N : п = 60 000 000 : 2772 = = 21645 руб. Все расчетные документы, в которых зафиксирована сумма, равная или превышающая величину шага отбора, обязательно попадут в выборку. Начало, отбора устанавливается произвольно. Рассмотрим в качестве примера записи по счету «Расчеты с покупателями» (табл. 7.11). Таблица 7.11 Формирование монетарной выборки (в качестве начала отбора принято 25 000 руб., шаг отбора равен 21 645)
Приведенный пример показывает, что число отобранных документов может быть значительно меньше объема выборки по числу отбираемых денежных единиц. Если сумма операций многократно превышает шаг отбора, мы получаем несколько раз указание на необходимость проверки этой операции (в примере операция 5 получила представительство в выборке шесть раз), и, наоборот, если сумма операции меньше шага отбора, она может не попасть в выборку (в примере это произошло с операцией 4). В целом чем крупнее операции по сравнению с шагом отбора, тем меньше будет совокупность отобранных документов - единиц наблюдения по сравнению с числом отобранных единиц. Особенности решения всех вопросов по определению репрезентативности выборки и распространению ее результатов на генеральную совокупность зависят от того, были ли выявлены ошибки в выборке или нет. Это влияет на значение коэффициента надежности: сохранится оно или нет. Исходя из этого проводится проверка соответствия фактической точности тому значению максимально допустимой суммарной величины ошибки, которое закладывалось при проектировании выборки. Если фактическая точность меньше или равна принятой, то выборка признается репрезентативной, если превышает ее, то применяются специальные методы оценки данных. Проверка производится на основе соотношения
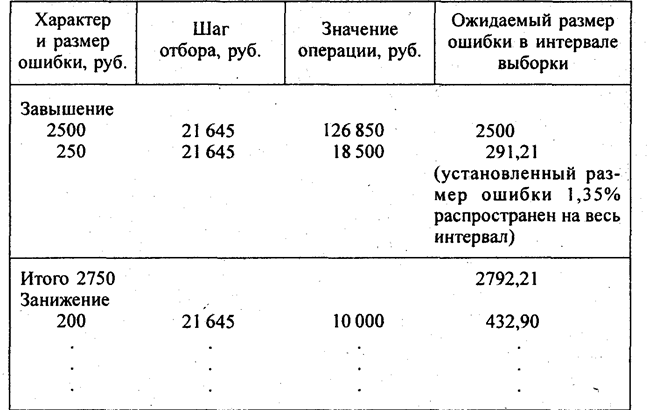
отсюда Если при проверке отобранных документов ошибок не обнаружено, то с принятой доверительной вероятностью мы можем распространить результаты выборки на всю генеральную совокупность и считать, что итог по генеральной совокупности не завышен более чем на величину предельно допустимой ошибки. Если же обнаружена по крайней мере одна ошибка, то первоначальная гипотеза относительно отсутствия ошибок, которая закладывалась при планировании выборки, оказывается несостоятельной. В этом случае должны быть пересмотрены либо значение коэффициента надежности, либо величина предельно допустимой ошибки (точность), либо и то, и другое. Если ошибки выявлены в операциях, значение которых превышает величину шага отбора, то можно быть уверенным в отношении абсалютного размера ошибок в таких операциях, так как каждая из них проверялась полностью. В этом случае нужно решить вопрос о распространении абсолютного размера выявленных ошибок на операции, значение которых меньше шага отбора. Все ошибки группируются в два класса: завышение суммы и ее занижение. Для всех операций, значение которых превышает шаг отбора, выявленная ошибка является точным размером завышения или занижения. Для операций, значение которых меньше шага отбора, размер выявленной ошибки относится, к значению операции, и полученная относительная ошибка умножается на шаг отбора, т. е. распространяется на весь интервал. Приведем пример (табл. 7.12). Таблица 7.12 Расчет суммарной ошибки на основе распространения результатов выборки
После определения суммарного размера ожидаемой ошибки по всем интервалам выборки (т. е; шагам отбора) производится сравнение с допустимым размером суммарной ошибки, и если рассчитанная суммарная ошибка превосходит допустимую величину, то, подставляя первую в формулу объема выборки, определяют, с каким коэффициентом надежности и соответственно с какой доверительной вероятностью могут гарантироваться результаты данного выборочного исследования:
Как известно, в экономических исследованиях обычно принимают доверительную вероятность не ниже 90%. Использование выборного метода в работе аудитора резко повышает эффективность получения результатов и приводит к экономии финансовых и трудовых затрат. Рекомендуемая литература к главе 7 1. Афифи А., Эйзен С. Статистический анализ. Подход с использованием ЭВМ/Пер, с англ.; Под ред. Г. П. Башарина. - М.: Мир, 1982. 2. Бокун Н. Ч., Чернышева Н. М. Методы выборочных обследований. -Минск: Министерство статистики и анализа Республики Беларусь. НИИ статистики, 1997. 3. Головач А. В., Ерша А. М., Трофимов В. П. Критерии математической статистики в экономических исследованиях. - М.: Статистика, 1973. 4. Джессен Р. Методы статистических обследований/Пер, с англ.; Под ред. и с предисл. Е. М. Четыркина. - М.: Финансы и статистика, 1985. 5. Дружинин Н. К. Математическая статистика в экономике. - М.: Статистика, 1971. 6. Информатика в статистике: словарь-справочник. - М., Финансы и статистика, 1994. 7. Йейтс Ф. Выборочный метод в переписях и обследованиях. - М.: Статистика, 1965. 8. Закс Л. Статистическое оценивание / Пер. с нем.; Под ред. и с предисл. Ю. П. Адлера и В. Г. Горского. - М.: Статистика, 1976. 9. Кокрен У. Методы выборочного исследования/Пер, с англ.; Под ред. А. Г. Волкова. - М.: Статистика, 1976. 10. Паниотто В. И. Качество социологической информации (Методы оценки и процедуры обеспечения). - Киев: Наукова думка, 1986. 11. Фишер Р. А. Статистические методы для исследователей: Пер. с англ. - М.: Госстатиздат, 1958. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

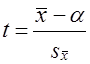 , (7.36)
, (7.36)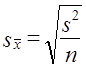 - при большой выборке;
- при большой выборке;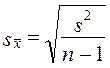 - при малой выборке.
- при малой выборке.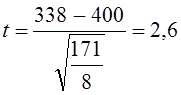 .
.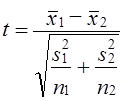 . (7.37)
. (7.37)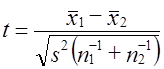 , (7.38)
, (7.38)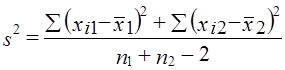 . (7.39)
. (7.39)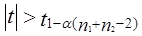
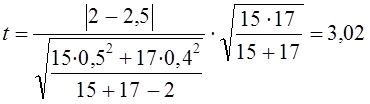 .
. 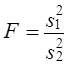 .
.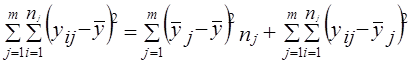 ,
,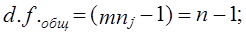
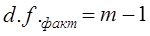 ;
;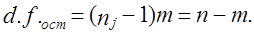
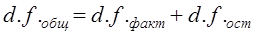
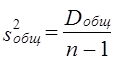 ,
,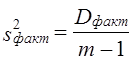 , (7.43)
, (7.43)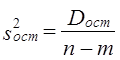 .
.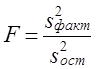 .
. 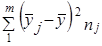
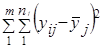
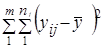
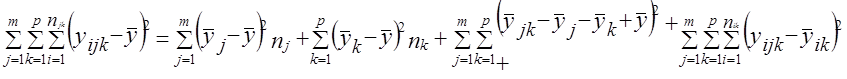 (7.44)
(7.44)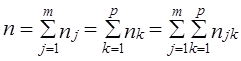
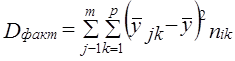 (7.48)
(7.48)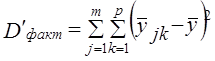 ;
; 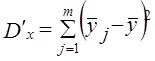 ; (7.49)
; (7.49)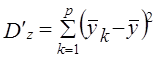 ;
;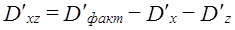 .
.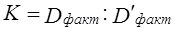 (7.50)
(7.50)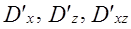 , на основе которых проводят расчет F-критериев:
, на основе которых проводят расчет F-критериев: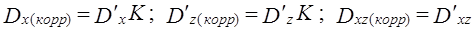 (7.50)
(7.50)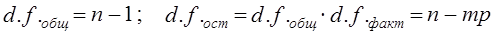 (7.51)
(7.51)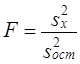
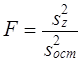
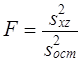
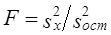 с
с 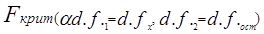 .
. 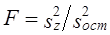 c
c 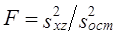 c
c 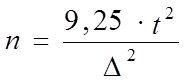 .
.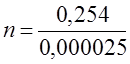 = 40 000 наблюдений.
= 40 000 наблюдений.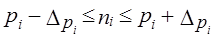
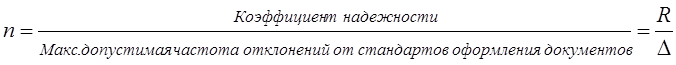
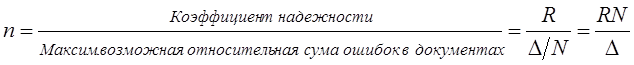
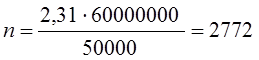 денежные единицы
денежные единицы