| Главная » Учебно-методические материалы » СТАТИСТИКА » Общая теория статистики: учебник. Под ред. Елисеевой И.И. |
| 23.01.2012, 16:54 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
8.11. Множественное уравнение регрессииПроблемы множественного корреляционно-регрессионного анализа и моделирования подробно изучаются в специальном курсе того же названия. В курсе «Общая теория статистики» рассматриваются только самые общие вопросы этой сложной проблемы и дается начальное представление о методике построения уравнения множественной регрессии и показателей связи. Рассмотрим линейную форму многофакторных связей не только как наиболее простую, но и как форму, предусмотренную пакетами прикладных программ для ПЭВМ. Если же связь отдельного фактора с результативным признаком не является линейной, то производят линеаризацию уравнения путем замены или преобразования величины факторного признака. Общий вид многофакторного уравнения регрессии имеет вид:
где k - число факторных признаков. Чтобы упростить систему уравнений МНК, необходимую для вычисления параметров уравнения (8.32), обычно вводят величины отклонений индивидуальных значений всех признаков от средних величин этих признаков.
Получаем систему k уравнений МНК:
Решая эту систему, получаем значения коэффициентов условно-чистой регрессии b. Свободный член уравнения вычисляется по формуле
Термин «коэффициент условно-чистой регресии» означает, что каждая из величин bj измеряет среднее по совокупности отклонение результативного признака от его средней величины при отклонении данного фактора хj от своей средней величины на единицу его измерения и при условии, что все прочие факторы, входящие в уравнение регрессии, закреплены на средних значениях, не изменяются, не варьируют. Таким образом, в отличие от коэффициента парной регрессии коэффициент условно-чистой регрессии измеряет влияние фактора, абстрагируясь от связи вариации этого фактора с вариацией остальных факторов. Если было бы возможным включить в уравнение регрессии все факторы, влияющие на вариацию результативного признака, то величины bj. можно было бы считать мерами чистого влияния факторов. Но так как реально невозможно включить все факторы в уравнение, то коэффициенты bj. не свободны от примеси влияния факторов, не входящих в уравнение. Включить все факторы в уравнение регрессии невозможно по одной из трех причин или сразу по ним всем, так как: 1) часть факторов может быть неизвестна современной науке, познание любого процесса всегда неполное; 2) по части известных теоретических факторов нет информации либо таковая ненадежна; 3) численность изучаемой совокупности (выборки) ограничена, что позволяет включить в уравнение регрессии ограниченное число факторов. Коэффициенты условно-чистой регрессии bj. являются именованными числами, выраженными в разных единицах измерения, и поэтому несравнимы друг с другом. Для преобразования их в сравнимые относительные показатели применяется то же преобразование, что и для получения коэффициента парной корреляции. Полученную величину называют стандартизованным коэффициентом регрессии или β-коэффициентом.
β-коэффициент при факторе хj, определяет меру влияния вариации фактора хj на вариацию результативного признака у при отвлечении от сопутствующей вариации других факторов, входящих в уравнение регрессии. Коэффициенты условно-чистой регрессии полезно выразить в виде относительных сравнимых показателей связи, коэффициентов эластичности:
Коэффициент эластичности фактора хj говорит о том, что при отклонении величины данного фактора от его средней величины на 1% и при отвлечении от сопутствующего отклонения других факторов, входящих в уравнение, результативный признак отклонится от своего среднего значения на ej процентов от у̅. Чаще интерпретируют и применяют коэффициенты эластичности в терминах динамики: при увеличении фактора х.на 1% его средней величины результативный признак увеличится на е. процентов его средней величины. Рассмотрим расчет и интерпретацию уравнения многофакторной регрессии на примере тех же 16 хозяйств (табл. 8.1). Результативный признак - уровень валового дохода и три фактора, влияющих на него, представлены в табл. 8.7. Напомним еще раз, что для получения надежных и достаточно точных показателей корреляционной связи необходима более многочисленная совокупность. Таблица 8.7 Уровень валового дохода и его факторы
Таблица 8.8 Показатели уравнения регрессии
Решение проведено по программе «Microstat» для ПЭВМ. Приведем таблицы из распечатки: табл. 8.7 дает средние величины и средние квадратические отклонения всех признаков. Табл. 8.8 содержит коэффициенты регрессии и их вероятностную оценку: первая графа «var» - переменные, т. е. факторы; вторая графа «regression coefficient» - коэффициенты условно-чистой регрессии bj; третья графа «std. errror» - средние ошибки оценок коэффициентов регрессии; четвертая графа - значения t-критерия Стьюдента при 12 степенях свободы вариации; пятая графа «prob» - вероятности нулевой гипотезы относительно коэффициентов регрессии; шестая графа «partial r2» — частные коэффициенты детерминации. Содержание и методика расчета показателей в графах 3-6 рассматриваются далее в главе 8. «Constant» - свободный член уравнения регрессии a; «Std. error of est.» - средняя квадратическая ошибка оценки результативного признака по уравнению регрессии. Было получено уравнение множественной регрессии: у̂ = 2,26x1 - 4,31х2 + 0,166х3 - 240. Это означает, что величина валового дохода на 1 га сельхозугодий в среднем по совокупности возрастала на 2,26 руб. при увеличении затрат труда на 1 ч/га; уменьшалась в среднем на 4,31 руб. при возрастании доли пашни в сельхозугодиях на 1% и увеличивалась на 0,166 руб. при росте надоя молока на корову на 1 кг. Отрицательная величина свободного члена вполне закономерна, и, как уже отмечено в п. 8.2, результативный признак - валовой доход становится нулевым задолго до достижения нулевых значений факторов, которое в производстве невозможно. Отрицательное значение коэффициента при х^ - сигнал о существенном неблагополучии в экономике изучаемых хозяйств, где растениеводство убыточно, а прибыльно только животноводство. При рациональных методах ведения сельского хозяйства и нормальных ценах (равновесных или близких к ним) на продукцию всех отраслей, доход должен не уменьшаться, а возрастать с увеличением наиболее плодородной доли в сельхозугодиях - пашни. На основе данных предпоследних двух строк табл. 8.7 и табл. 8.8 рассчитаем р-коэффициенты и коэффициенты эластичности согласно формулам (8.34) и (8.35). Как на вариацию уровня дохода, так и на его возможное изменение в динамике самое сильное влияние оказывает фактор х3 - продуктивность коров, а самое слабое - х2 - доля пашни. Значения Р2/ будут использоваться в дальнейшем (табл. 8.9); Таблица 8.9 Сравнительное влияние факторов на уровень дохода
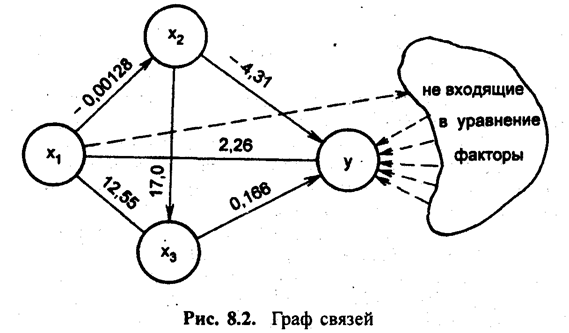
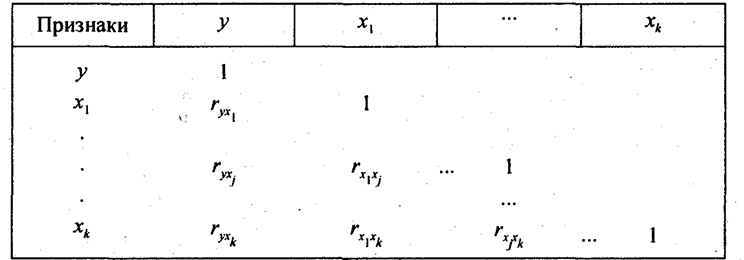
Итак, мы получили, что β-коэффициент фактора хj относится к коэффициенту эластичности этого фактора, как коэффициент вариации фактора к коэффициенту вариации результативного признака. Поскольку, как видно по последней строке табл. 8.7, коэффициенты вариации всех факторов меньше коэффициента вариации результативного признака; все β-коэффициенты меньше коэффициентов эластичности. Рассмотрим соотношение между парным и условно-чистым коэффициентом регрессии на примере фактора -с,. Парное линейное уравнение связи у с х, имеет вид: ŷ = 3,886x1 – 243,2 Условно-чистый коэффициент регрессии при x1, составляет только 58% парного. Остальные 42% связаны с тем, что вариации x1 сопутствует вариация факторов x2 x3, которая, в свою очередь, влияет на результативный признака. Связи всех признаков и их коэффициенты парных регрессий представлены на графе связей (рис. 8.2). Если сложить оценки прямого и опосредованного влияния вариации х1 на у, т. е. произведения коэффициентов парных регрессий по всем «путям» (рис. 8.2), получим: 2,26 + 12,55·0,166 + (-0,00128)·(-4,31) + (-0,00128)·17,00·0,166 = 4,344. Эта величина даже больше парного коэффициента связи x1 с у. Следовательно, косвенное влияние вариации x1 через не входящие в уравнение признаки-факторы - обратное, дающее в сумме: 3,886 - 4,344 = - 0,458. 8.12. Меры тесноты связей в многофакторной системеМногофакторная система требует уже не одного, а множества показателей тесноты связей, имеющих разный смысл и применение. Основой измерения связей является матрица парных коэффициентов корреляции (табл. 8.10). Таблица 8.10 Матрица парных коэффициентов корреляции
По этой матрице можно судить о тесноте связи факторов с результативным признаком и между собой. Хотя все эти показатели относятся к парным связям, все же матрицу можно использовать для предварительного отбора факторов для включения в уравнение регрессии. Не рекомендуется включать в уравнение факторы слабо связанные с результативными признаками, но тесно связанные с другими факторами. Если, например, имеем: rxy1 = 0,8; rxy2 = 0,65; rx1x2 = 0,88, то в регрессионное уравнение следует включить фактор x1, а фактор х2 не включать, так как он тесно связан с х1 (коллинеарен с x1), и его корреляция с у слабее, чем корреляция фактора x1. Совершенно недопустимо включать в анализ факторы, функционально связанные друг с другом, т. е. с коэффициентом корреляции, равным единице. Включение таких пар признаков приводит к вырожденной матрице коэффициентов и неопределенности решения. В этом случае решение задачи на ПЭВМ прекращается. Матрица парных коэффициентов для нашего примера (табл. 8.11) говорит об отсутствии коллинеарных (т. е. линейно связанных) факторов, что позволяет включить все эти факторы в уравнении регрессии. На основе этой матрицы вычисляется наиболее общий показатель тесноты связи всех входящих в уравнение регрессии факторов Таблица 8.11 Матрица парных коэффициентов корреляции
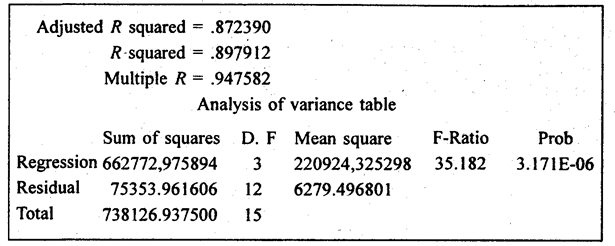
Этим способом можно определить величину R2 не вычисляя расчетных значений результативного признака у̂i для всех единиц совокупности. Если полученная величина R2 не удовлетворяет исследоветеля, то можно прекратить дальнейшие вычисления и не рассчитывать у̂i (это имеет значение, если совокупность состоит из сотен и тысяч единиц). Принципиальное содержание множественного коэффициента детерминации, как и парного, раскрывается формулой (8.2). Jmo отношение части вариации результативного признака, объясняемой за счет вариации входящих в уравнение факторов, к общей вариации результативного признака за счет всех факторов, здесь под «вариацией» понимается сумма квадратов отклонении индивидуальных расчетных по уравнению величин от средней («объясненная вариация») и первичных индивидуальных величин от средней («общая вариация»). В нашем примере значение сумм квадратов отклонений и коэффициенты детерминации и корреляции приведены по распечатке программы «Microstat» в табл. 8.12. Таблица 8.12 Показатели множественной корреляционной связи
Верхняя строка: корректированный R-квадрат = 0,872390; вторая строка: R-квадрат = 0,897912; третья строка: множественный R = 0,947582. Затем приводится таблица дисперсионного анализа, в которой указываются источники вариации: объясненная сумма квадратов отклонений значений, рассчитанных по уравнению регрессии, от среднего значения Dост = S(ŷi - y̅)2 = 662 772,98 при числе степеней свободы, равном числу объясняющих переменных dfk = 3; остаточная - отклонения фактических значений от расчетных Dост = S(ŷi - y̅)2 = 75353,96 при числе степеней свободы, равном df=n-k-1, df=12; общая - S(ŷi - y̅)2 =738 126,94, при числе степеней свободы df = п –k - 1, df = 15. Затем приводится средний квадрат отклонений: s21 = Dобъясн : dfобъясн = 662772,98 : 3 = 220924,3; Ы22 =Dост : dfост = 75353,96 : 12 = 6279,5. Далее указано их отношение, т. е. s21/s22 = F-критерию. Наконец, указывается вероятность ошибочного решения, т. е. нулевого R2, равная 0,000003171. Три фактора, включенные в уравнение регрессии, объясняют 89,8% вариации уровня валового дохода, если рассматривать 16 хозяйств как генеральную совокупность, не считаясь с ее ограниченной численностью (некорректированный коэффициент детерминации равен 0,8979). Если же учесть конечность объема совокупности п, число факторов k, а также свойство метода, по которому по мере приближения числа k к числу п коэффициент детерминации автоматически приближается к единице и достигает ее при k = п - 1 независимо от реальной роли факторов, то необходимо корректировать коэффициент множественной детерминации на потерю степеней свободы вариации:
Корректированный коэффициент детерминации всегда ниже, чем некорректированный, причем разность их значений тем меньше, чем меньше факторов входит в уравнение регрессии. Если из числа факторов исключить факторы, слабо связанные с результативным признаком (т. е. с низким значением βj, например, β < 0,1), то некорректированный коэффициент детерминации немного уменьшится (он всегда уменьшается при исключении части факторов), но корректированный коэффициент может даже возрасти за счет уменьшения разности между R2 и корректированным R2. Что касается множественного коэффициента корреляции R, то программа «Microstat» рассчитывает его, как корень квадратный из некорректированного R2, а другие программы, например «Statgraphics», - как корень квадратный из R2корр. Для случая двух факторов коэффициент множественной детерминации легко вычисляется по рекуррентной формуле из парных коэффициентов детерминации:
Используя матрицу парных коэффициентов корреляции (табл. 8.11), получим:
Таким образом, за счет вариации факторов x1 и х2 объясняется 57,65% общей вариации валового дохода с 1 га сельхозугодий. Вернемся к табл. 8.12. Дисперсионный анализ системы связей предназначен для оценки того, насколько надежно доказывают исходные данные наличие связи результативного признака со всеми факторами, входящими в уравнение. Для этого сравниваются дисперсии у - объясненная и остаточная: суммы соответствующих квадратов отклонений, приходящиеся на одну степень свободы вариации. Отношение дисперсии за счет факторов к остаточной дисперсии есть критерий Фишера F; в нашем примере он равен 35,18. Табличное критическое значение для 3 и 12 степеней свободы при вероятности нулевой гипотезы 0,01 составляет 5,95. Следовательно, вероятность нулевой гипотезы много меньше 0,01. Программа «Microstat» дает значение вероятности нулевой гипотезы, т. е. вероятность случайного отклонения от нуля коэффициента детерминации при отсутствии связи в генеральной совокупности; она равна 3,17·10-6, т. е. три миллионных! Ясно, что эту ничтожную вероятность можно игнорировать и сделать вывод, что имеющаяся информация надежно свидетельствует о наличии связи. Кроме показателя общей тесноты связи вариации результативного признака со всеми факторами, входящими в регрессионное уравнение, необходимы и показатели, измеряющие тесноту связи с каждым фактором. К таким показателям относятся коэффициенты раздельной детерминации. Коэффициентом раздельной детерминации, обозначаемым далее как d2j, называется произведение парного коэффициента корреляции фактора хj на его β-коэффициент.
Формула (8.39) дает еще один метод вычисления коэффициента множественной детерминации, используемый в некоторых программах для ЭВМ. В нашем примере получаем следующие значения коэффициентов раздельной детерминации:
Таким образом, за счет вариации x1 объясняется 24,2% вариации, за счет вариации х2 - всего 7,3%; за счет вариации x3 - более половины - 583% вариации уровня дохода. Сумма коэффициентов раздельной детерминации равна некорректированному коэффициенту R2. Недостатком коэффициентов раздельной детерминации является их гетерогенный характер: то, что они объединяют коэффициент парной корреляции, измеряющий нечистое влияние фактора, с β-коэффициентом, измеряющим условно чистое влияние фактора, абстрагированное от влияния других факторов, входящих в уравнение связи. Из-за этого могут возникнуть неинтерпретируемые отрицательные величины коэффициентов d2j, если знаки парного коэффициента корреляции и β-коэффициента не совпадают при существенной взаимосвязи между факторами. Кроме того, сама идея о том, что совокупное влияние всех факторов равно сумме влияния каждого из них, противоречит системному подходу к исследованию. Рассмотрим разложение R2 с учетом системного эффекта. Система факторов - это не простая их сумма, так как система предполагает внутренние связи, взаимодействие составляющих ее элементов. Действие системы не равно сумме воздействий составляющих ее элементов. К последним добавляется «системный эффект» «Emergency». Методом, полностью отвечающим системному подходу, является метод разложения коэффициента множественной детерминации на сумму чистых влияний каждого фактора, выражаемых величинами β21, и показатель влияния системного эффекта факторов ηx. Так как расчетные значения результативного признака у̂j можно представить как
Подставим в (8.40) значение фактора xm-1 = xm +Dxm1 : Теперь измерим сумму квадратов отклонений у только за счет вариации признака хm.
Мерой вариации результативного признака за счет изолированного влияния вариации фактора xm является доля объясняемой этим влиянием вариации у. Соответственно получаем: Сумма изолированных долей влияния каждого фактора в отдельности на вариацию у есть
Проведем разложение коэффициента множественной детерминации по данным нашего примера: за счет вариации x1 : β21, = 0,35222 = 0,1239, или 12,39%; за счет вариации x2 : β22 = (-0.206)2 = 0,0424, или 4,24%; за счет вариации x3 : β23, = 0,6642 = 0,4409, или 44,09%. Суммарное влияние трех факторов составило
Как видим, роль системного эффекта связей между факторами довольно велика: он на втором месте после влияния третьего фактора. Системный эффект может, в свою очередь, быть разложен на влияние ковариации каждой пары факторов или на влияние совместной вариации отдельных групп факторов, если число последних велико. Если исследователь все же желает отказаться от выделения системного эффекта, свести коэффициент множественной детерминации к сумме по отдельным факторам, можно разделить величину П, пропорционально величине β2j. Программы анализа связей на ЭВМ обычно предусматривают вычисление коэффициентов частной детерминации. Они приведены выше в последней графе табл. 8.8. Коэффициент частной детерминации фактора xm - это доля вариации у, дополнительно объясняемой при включении фактора xm после остальных факторов в уравнение регрессии, в величине вариации у, не объясненной ранее включенными факторами. Наиболее ясно суть частных коэффициентов детерминации выражается формулой их расчета через коэффициенты множественной детерминации. Частный коэффициент детерминации для фактора хm обозначим как Тогда Здесь R2y - коэффициент детерминации для уравнения со всеми k факторами. Числитель (8.43) и есть дополнительно объясняемая часть вариации у при включении фактора хm в уравнение после всех остальных факторов. В нашем примере, используя ранее рассчитанную величину Ryx1x2 = 0,5765, при включении в анализ фактора x3 получаем: Некоторое расхождение в четвертой значащей цифре с табл. 8.8 объясняется округлением промежуточных расчетных показателей. Следует усвоить, что коэффициенты частной детерминации - это доли от разных величин, поэтому они несравнимы; по этим долям нельзя судить о роли факторов. Их главное практическое значение - определить, имеет ли смысл добавить в уравнение регрессии новый фактор или нет. Если при его включении ранее необъясненная вариация уменьшится на три четверти, как в примере при введении фактора х3, его включение оправдано; если же коэффициент частной детерминации мал, то дополнительный фактор включать не следует. Сумма частных коэффициентов детерминации смысла не имеет и растет с ростом числа факторов и ростом R2 без ограничения. При последовательном вводе факторов в уравнение регрессии объясняемая часть вариации результативного признака возрастает с каждым новым фактором, вводимым в уравнение. При вводе последнего фактора эта часть достигает величины R2. Доли вариации у, объясняемые вводом каждого следующего фактора, и называют коэффициентами последовательной детерминации. Обозначим их как р2j. Для первого фактора этот коэффициент равен коэффициенту парной детерминации первого фактора, для второго - разности между коэффициентом детерминации при двух факторах и парным коэффициентом детерминации первого фактора и так далее. По данным нашего примера имеем:
Однако крупнейшим недостатком такого способа разложения R2 является зависимость величин р2j от принятого порядка включения факторов в уравнение регрессии. Первый включаемый фактор «забирает в свою пользу» львиную часть системного эффекта, а на долю последнего фактора остается ничтожная часть. Например, если переставить местами факторы х1 и х3, а также вычислить по рекуррентной формуле двухфакторный коэффициент детерминации p21 (для фактора х1) = р22 (для фактора x2) = р23 (для фактора x3) = Доля фактора x3 возросла более чем вдвое, а доля фактора x1 уменьшилась более чем втрое. 8.13. Вероятностные оценки параметров множественной регрессии и корреляцииЕсли показатели многофакторной системы связи используются как оценки генеральных параметров, экстраполируются на другие значения факторов, как при прогнозировании, то значения параметров необходимо сопроводить вероятностными оценками, указать среднюю ошибку и доверительные границы параметра с заданной. вероятностью. Для парной корреляции эта проблема изложена в п. 8.5. В этом параграфе приводятся формулы средних ошибок репрезентативности для специфических параметров многофакторной системы. Средняя ошибка условно чистого коэффициента регрессии bp для фактора xp, обозначаемая mbp, имеет вид: где
где
Например, для фактора x1, имеем:
Отношение величины коэффициента регрессии к его средней ошибке есть t-критерий Стьюдента. В данном случае имеем: b1/mb1 = 2,26/0,6582 = 3,43. Критическое значение t для вероятности нулевой гипотезы 0,01 при 12 степенях свободы равно 3,05. Следовательно, надежно установлено, что генеральное значение коэффициента b1, не является нулевым, влияние (условно чистое) фактора x1, на вариацию у существенно. Доверительные границы коэффициента регрессии b1, с вероятностью 0,95, для которой значение критерия Стьюдента равно 2,18, составляют 2,26 ± 2,18·0,658 или от 0,826 до 3,694. Очень широкие границы объясняются малой численностью единиц совокупности. Из (8.44) следует, что при росте объема совокупности в q раз ошибка коэффициента регрессии, как и ошибка выборочной оценки средней величины, уменьшится в √q̅ раз. При 400 единицах совокупности ошибка была бы меньше в 5 раз. Если значение критерия t оказывается ниже критического для вероятности нулевой гипотезы 0,05, влияние фактора считается не доказанным надежно, и при работе программ ЭВМ с отсевом несущественных факторов по t-критерию данный фактор автоматически исключается из уравнения регрессии. Средняя ошибка оценки коэффициента множественной корреляции mR определяется по формуле Оценка существенности и расчет доверительных границ генерального коэффициента корреляции осуществляются так же, как и для коэффициента регрессии. Если значение R близко к единице, необходимо использовать преобразование Фишера, рассмотренное ранее в п. 8.2. Существуют также специальные таблицы критических значений коэффициента корреляции для заданного числа степеней свободы и вероятности нулевой гипотезы (см. приложение, табл. 5). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

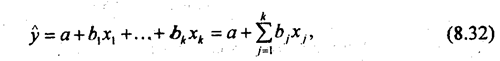
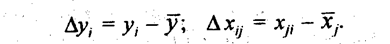
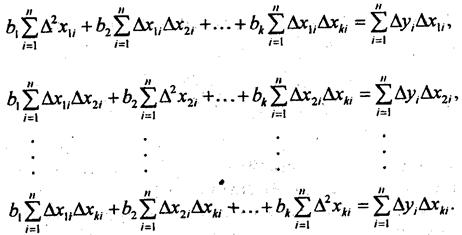






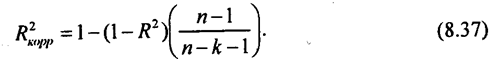
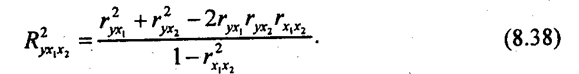
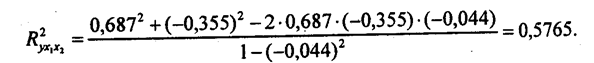
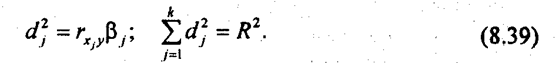
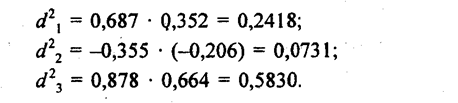
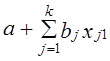 , то вариацию у̃j1 только за счет влияния фактора xm можно представить при условии, что все остальные факторы, входящие в уравнение, закреплены на своих средних уровнях:
, то вариацию у̃j1 только за счет влияния фактора xm можно представить при условии, что все остальные факторы, входящие в уравнение, закреплены на своих средних уровнях: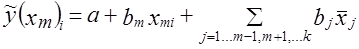 . (8.40)
. (8.40)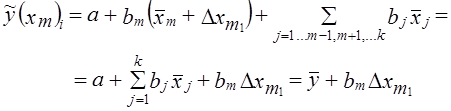
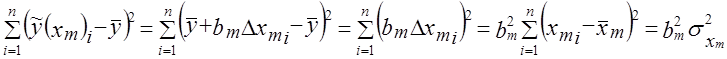 (8.41)
(8.41)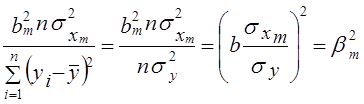
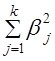 , a системный эффект
, a системный эффект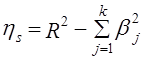 (8.42)
(8.42)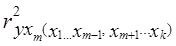 .
.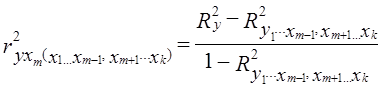 . (8.43)
. (8.43)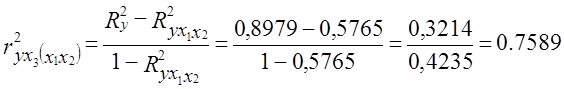
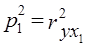 = 0,6872 = 0,4720;
= 0,6872 = 0,4720;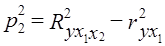 = 0,5765 - 0,4720 = 0,1045;
= 0,5765 - 0,4720 = 0,1045;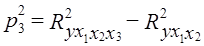 = 0,8979 - 0,5765 = 0,3214;
= 0,8979 - 0,5765 = 0,3214;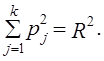
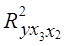 = 0,8035, то получим результаты, отличные от предыдущих:
= 0,8035, то получим результаты, отличные от предыдущих: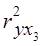 = 0,8782 = 0,7709;
= 0,8782 = 0,7709;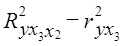 = 0,8035 - 0,7709 = 0,0326;
= 0,8035 - 0,7709 = 0,0326;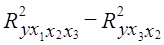 = 0,8979 - 0,8035 = 0,0944.
= 0,8979 - 0,8035 = 0,0944.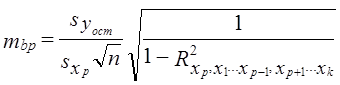 . (8.44)
. (8.44)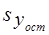 - оценка остаточного (не объясненного факторами) среднего квадратического отклонения результативного признака с учетом степеней свободы вариации:
- оценка остаточного (не объясненного факторами) среднего квадратического отклонения результативного признака с учетом степеней свободы вариации: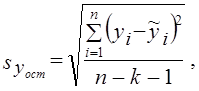
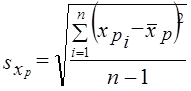 ,
,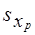 - оценка среднего квадратического отклонения при-знака xp.
- оценка среднего квадратического отклонения при-знака xp.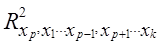 - коэффициент множественной детерминации для фактора xp, доля вариации фактора xp, связанная с вариацией других факторов.
- коэффициент множественной детерминации для фактора xp, доля вариации фактора xp, связанная с вариацией других факторов.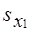 = 34,6.
= 34,6.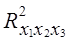 = 0,2433 - вычислен по рекуррентной формуле по данным табл. 8.11. Отсюда:
= 0,2433 - вычислен по рекуррентной формуле по данным табл. 8.11. Отсюда: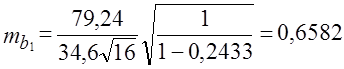
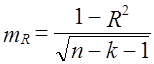 . (8.45)
. (8.45)