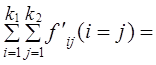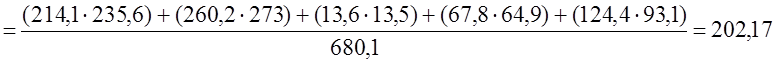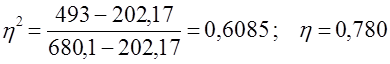| Главная » Учебно-методические материалы » СТАТИСТИКА » Общая теория статистики: учебник. Под ред. Елисеевой И.И. |
| 23.01.2012, 16:54 | |
8.14. Корреляционно-регрессивные модели (КРМ) и их применение в анализе и прогнозеКорреляционно-регрессионной моделью системы взаимосвязанных признаков является такое уравнение регрессии, которое включает основные факторы, влияющие на вариацию результативного признака, обладает высоким (не ниже 0,5) коэффициентом детерминации и коэффициентами регрессии, интерпретируемыми, в соответствии с теоретическим знанием о природе связей в изучаемой системе. Приведенное определение КРМ включает достаточно строгие условия: далеко не всякое уравнение регрессии можно считать моделью. В частности, полученное выше по 16 хозяйствам уравнение не отвечает последнему требованию из-за противоречащего экономике сельского хозяйства знака при факторе х2 - доля пашни. Однако в учебных целях используем его как модель. Теория и практика выработали ряд рекомендаций для построения корреляционно-регрессионной модели. 1. Признаки-факторы должны находиться в причинной связи с результативным признаком (следствием). Поэтому, недопустимо, например, в модель себестоимости у вводить в качестве одного из факторов хj коэффициент рентабельности, хотя включение такого «фактора» значительно повышает коэффициент детерминации. 2. Признаки-факторы не должны быть составными частями результативного признака или его функциями, о чем уже сказано ранее. 3. Признаки-факторы не должны дублировать друг друга, т. е. быть коллинеарными (с коэффициентом корреляции более 0,8). Так, не следует в модель производительности труда включать и энерговооруженность рабочих, и их фондовооруженность, так как эти факторы тесно связаны друг с другом в большинстве объектов. 4. Не следует включать в модель факторы разных уровней иерархии, т. е. фактор ближайшего порядка и его субфакторы. Например, в моделях себестоимости зерна не следует включать и урожайность зерновых культур, и дозу удобрений под них или затраты на обработку гектара, показатели качества семян, плодородия почвы, т. е. субфакторы самой урожайности. 5. Желательно, чтобы между результативным признаком и факторами соблюдалось единство единицы совокупности, к которой они отнесены. Например, если у - валовой доход предприятия, то и все факторы должны относиться к предприятию: стоимость производственных фондов, уровень специализации, численность работников и т. д. Если же у - средняя зарплата рабочего на предприятии, то факторы должны относиться к рабочему: разряд или классность, стаж работы, возраст, уровень образования, энерговооруженность и т. д. Правило это не категорическое, в модель зарплаты рабочего можно включить, например и уровень специализации предприятия. 6. Математическая форма уравнения регрессии должна соответствовать логике связи факторов с результатом в реальном объекте. Например, такие факторы урожайности, как дозы разных удобрений, уровень плодородия, число прополок и т. п., создают прибавки величины урожайности, мало зависящие друг от друга; уро-
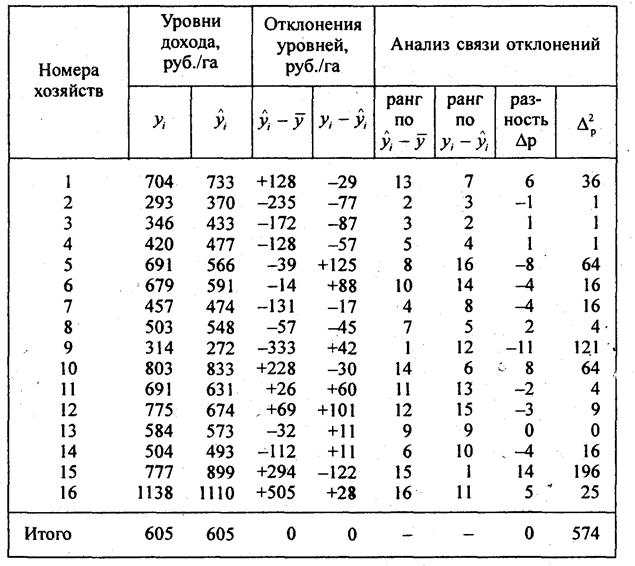
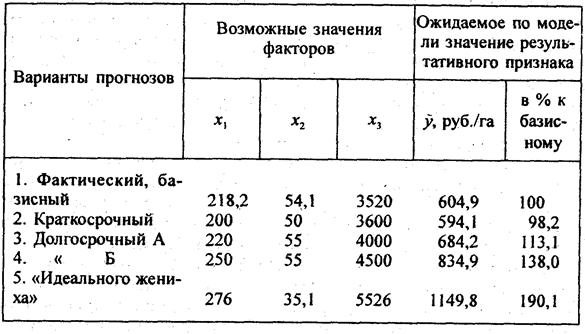
Первое слагаемое в правой части равенства - это отклонение, которое возникает за счет отличия индивидуальных значений факторов у данной единицы совокупности от их средних значений по совокупности. Его можно назвать эффектом факторообеспеченно-сти. Второе слагаемое - отклонение, которое возникает за счет не входящих в модель факторов и отличия индивидуальной эффективности факторов по данной единице совокупности от средней эффективности факторов в совокупности, измеряемой коэффициентами условно-чистой регрессии. Его можно назвать эффектом фа-тороотдачи. Рассмотрим пример расчета и анализа отклонений по ранее построенной модели уровня валового дохода в 16 хозяйствах. Знаки тех и других отклонений 8 раз совпадают и 8 раз не совпадают. Коэффициент корреляции рангов отклонений двух видов составил 0,156. Это означает, что связь вариации факторообеспеченности с вариацией фактороотдачи слабая, несущественная (табл. 8.13). Таблица 8.13 Анализ факторообеспеченности и фактороотдачи по регрессионной модели уровня валового дохода Обратим внимание на хозяйство № 15 с высокой факторообеспеченностью (15-е место) и самой худшей фактороотдачей (1-й ранг), из-за которой хозяйство недополучило по 122 руб. дохода с 1 га. Напротив, хозяйство № 5 имеет факторообеспеченность ниже средней, но благодаря более эффективному использованию факторов получило на 125 руб. дохода с 1 га больше, чем было бы получено при средней по совокупности эффективности факторов. Более высокая эффективность фактора х1 (затраты труда) может означать более высокую квалификацию работников, лучшую заинтересованность работников в качестве выполняемой работы. Более высокая эффективность фактора х3 с точки зрения доходности может состоять в высоком качестве молока (жирности, охлажденности), ввиду которого оно реализовано по более высоким ценам. Коэффициент регрессии при х2, как уже отмечено, экономически не обоснован. Использование регрессионной модели для прогнозирования состоит в подстановке в уравнение регрессии ожидаемых значений факторных признаков для расчета точечного прогноза результативного признака или (и) его доверительного интервала с заданной вероятностью, как уже сказано в 8.2. Сформулированные там же ограничения прогнозирования по уравнению регрессии сохраняют свое значение и для многофакторных моделей. Кроме того, необходимо соблюдать системность между подставляемыми в модель значениями факторных признаков. Формулы для расчета средних ошибок оценки положения гиперплоскости регрессии в заданной многомерной точке и для индивидуальной величины результативного признака весьма сложны, требуют применения матричной алгебры и здесь не рассматриваются. Средняя ошибка оценки значения результативного признака, рассчитанная по программе ПЭВМ «Microstat» и приведенная в табл. 8.8, равна 79,2 руб. на 1 га. Это лишь среднее квадратическое отклонение фактических значений дохода от расчетных по уравнению, не учитывающее ошибки положения самой гиперплоскости регрессии при экстраполяции значений факторных признаков. Поэтому ограничимся точечными прогнозами в нескольких вариантах (табл. 8.14). Для сравнения прогнозов с базисным уровнем средних по совокупности значений признаков введена первая строка таблицы. Краткосрочный прогноз рассчитан на малые изменения факторов за короткое время и снижение трудообеспеченности. Результат неблагоприятен, доход снижается. Долгосрочный прогноз А - «осторожный», он предполагает весьма умеренный прогресс факторов и соответственно небольшое увеличение дохода. Вариант Б - «оптимистический», рассчитан на существенное изменение факторов. Вариант № 5 построен по способу, которым Агафья Тихоновна в комедии Н. В. Гоголя «Женитьба» мысленно конструирует портрет «идеального жениха»: нос взять от одного претендента, подбородок от другого, рост от третьего, характер от четвертого... вот если бы соединить все нравящиеся ей качества в одном человеке, она бы не колеблясь вышла замуж... Так и при прогнозировании мы объединяем лучшие (с точки зрения модели дохода) наблюдаемые значения факторов: берем значение x1 от хозяйства № 10, значение x2 от хозяйства № 2, значение х3 от хозяйства №16. Все значения факторов уже существуют реально в изучаемой совокупности, они не «ожидаемые», не «взятые с потолка», это хорошо. Однако могут ли эти значения факторов сочетаться в одном предприятии, системны ли эти значения? Решение данного спорного вопроса выходит за рамки статистики, оно требует конкретных знаний об объекте прогнозирования. Таблица 8.14 Прогнозы валового дохода по регрессионной модели
8.15. Измерение связи неколичественных признаковКорреляционно-регрессионный метод применим только к количественным признакам. Однако задача измерения связи ставится перед статистикой и по отношению к таким признакам, как пол, образование, занятие, семейное состояние человека, отрасль, форма собственности предприятия, т. е. признакам, не имеющим количественного выражения. Учеными разных стран за последние сто лет разработано несколько методов измерения связей таких признаков. Отметим прежде всего уже рассмотренный ранее коэффициент корреляции рангов Спирмена, применимый и к количественным, и неколичественным, но поддающимся ранжированию признакам. Так, например, можно при помощи одной группы экспертов проранжировать кандидатов на занятие какой-либо должности по степени профессиональной подготовленности, а другую группу экспертов просить проранжировать тех же кандидатов по личностным и этическим качествам, а затем измерить связь между рангами. Важным частным случаем задачи является измерение связи при альтернативной вариации двух признаков, один из которых имеет характер причины, а другой - следствия. Например, при социологическом обследовании 1000 жителей города были поставлены два вопроса: 1. Считаете ли вы, что ваши доходы позволяют обеспечивать удовлетворение основных потребностей? 2. Удовлетворяет ли вас деятельность мэра города? Можно предположить, что причиной отрицательного ответа на второй вопрос у части населения является неудовлетворенность их потребностей доходами, т.е. имеется связь между ответами на оба вопроса. Для измерения этой связи составляют двухмерное (дихотомическое) распределение ответов 2х2, приведенное в табл. 8.15. Таблица 8.15 Взаимосвязь между ответами на два вопроса социологического обследования
Если бы все, ответившие «да» на 1-й вопрос, отвечали бы «да» на 2-й вопрос, и так же совпадали ответы «нет», то связь была бы предельно тесной, функциональной. Но на самим деле распределение ответов на оба вопроса не совпадает. Большая часть ответивших «да» на 1-й вопрос ответила «да» и на 2-й вопрос, но часть ответила «нет». То же относится к ответившим «да» на 2-й вопрос. Связь есть, но неполная, типа корреляционной, и нужно измерить тесноту этой связи. К. Пирсон предложил показатель, названный коэффициентом ассоциации. В числителе этого относительного показателя разность произведения чисел с одинаковыми ответами на оба вопроса: да-да и нет-нет и произведения чисел с неодинаковыми ответами: да-нет И нет-да. В знаменателе коэффициента ассоциации - корень квадратный из произведения всех четырех частных итогов. В буквенных обозначениях по табл. 8.13 имеем: Свойства коэффициента ассоциации такие же, как и у коэффициента корреляции: коэффициент ассоциации обращается в нуль, если оба произведения в числителе точно уравновешиваются (что крайне маловероятно); он равен плюсединице, если отсутствуют оба гетерогенных сочетания Аb и Ba; равен минус единице, если отсутствуют гомогенные сочетания ответов Аа и Bb. Другой метод измерения связи по «четырехклеточной таблице» предложен английскими статистиками Эдни Дж. Юлом (1871-1951) и Морисом Дж. Кендэлом (1907). Числитель этого коэффициента, называемого коэффициентам контингенции, совпадает с числителем коэффициента ассоциации Пирсона, а в знаменателе - сумма тех же произведений, разность которых стоит в числителе:
Как видим, коэффициент Юла-Кендэла значительно выше, чем коэффициент Пирсона. Крупный недостаток данного коэффициента в том, что уже при равенстве нулю только одного из двух гетерогенных сочетаний - либо Аb, либо Bа коэффициент Юла - Кендэла обращается в единицу. Можно сказать, что этот показатель очень либерально оценивает тесноту связи, завышает ее. Наконец, вполне возможно предложить показатель тесноты связи в форме отношения избытка суммы гомогенных сочетаний над их пропорциональной суммой к предельно возможному избытку. Для этого необходимо вначале вычислить, каковы были бы пропорциональные числа гомогенных сочетаний Аа и Bb? Пропорциональные числа - это доли от общей численности совокупности «N», которые были бы получены при полном отсутствии взаимосвязи группировок по двум признакам (ответам на два вопроса), т. е. числа (SA·Sa:N) и (SB·Sb:N), составляющие по данным табл. 8.13: При отсутствии связи на первой диагонали таблицы в сумме было бы 100 + 450 = 550 единиц совокупности, а на самом деле их 170 + 520 = 690. Избыток, образовавшийся ввиду прямой связи между ответами, составил 690—550 = 140. Предельно возможный избыток был бы в том случае, если бы не было гетерогенных сочетаний, т. е. Аb и Bа. Он составляет 140+80 + 230 = 450. Сам же показатель тесноты связи - отношение фактического излишка к предельному: 140 : 450 =0,311. Как видим, этот показатель близок к коэффициенту ассоциации, но обладает чрезвычайно логичной и ясной интерпретацией: связь составляет 0,311 или 31,1%, от предельно возможной функциональной. Этот показатель - аналог не коэффициента корреляции, а коэффициента детерминации. Поэтому правомерно обозначить его как R2 или η2 . Он имеет вид: где Подставляя эти выражения в (8.49), получим:
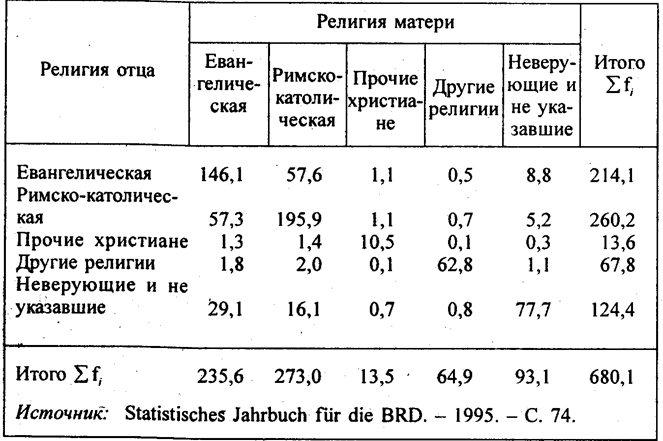
При наличии не двух, а более возможных значений каждого из взаимосвязанных признаков также разработаны разные методы измерения тесноты связи. Рассмотрим некоторые из этих мер на примере изучения влияния религиозной принадлежности на формирование супружеских пар. Воспользуемся данными ФРГ, где такой учет ведется постоянно. Статистический ежегодник Федеративной Республики Германии приводит распределение живорожденных младенцев по религиозной принадлежности отца и матери. При этом выделены 5 групп по религиозной принадлежности граждан: евангелическая (в России их чаще именуют протестантами); 2) римско-католическая; 3) прочие христиане (включая и православных); 4) других религий; 5) неверующие или не указавшие религиозную принадлежность (табл. 8.16). Таблица 8.16 Распределение новорожденных в ФРГ по религиозной принадлежности отца и матери в 1993 г. (тыс. чел.)
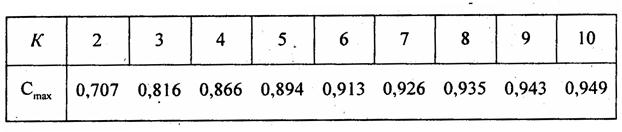
В табл. 8.16 представлена «решетка» 5 ´ 5, и все ее клетки не пусты: встречаются детные браки между лицами любых вероисповеданий. Но при этом наибольшие числа располагаются вдоль «главной диагонали», т. е. явно преобладают случаи, когда и отец и мать Таблица 8.17 Предельные значения коэффициента Пирсона
По данным табл. 8.16 имеем:
Таким образом, за счет предпочтения браков между лицами одинаковых религий на главную диагональ «собралось» 60,85% возможных родительских пар сверх равномерного распределения: связь составила 60,85% предельно тесной. Итак, все способы измерения показали, что влияние религии на формирование супружеских пар в ФРГ в 1993 году было значительное. Если кроме количественных факторов при многофакторном регрессионном анализе включается и неколичественный, то применяют следующую методику: наличие неколичественного фактора у единиц совокупности обозначают единицей, его отсутствие -нулем. Если таких факторов, или градаций неколичественного фактора несколько, в уравнение регрессии вводятся несколько так называемых «фиктивных переменных», принимающих значения либо единицы, либо нуля. Например, пусть имеется три количественных фактора урожайности (x1, x2, x3) и три природных зоны. В ЭВМ вводятся переменные в порядке их принадлежности к той или иной зоне (табл. 8.18). Линейное уравнение регрессии будет иметь вид: ŷ = a +b1x1 + b2x2 + b3x3 + b4u1 + b5u2 (8.57) Величина коэффициента b4 означает, что все единицы II зоны при тех же значениях количественных факторов, как и единицы I зоны, будут в среднем иметь значение у̂ на b4 больше (или меньше, если b4 < 0), чем единицы совокупности I зоны. Величина b5 озна-
Таблица 8.18
Рекомендуемая литература к главе 8 1. Антон Г. Анализ таблиц сопряженности / Пер. с англ. - М.: Финансы и статистика, 1982. 2. Елисеева И. И. Статистические методы измерения связей. -Л.: Изд-во Ленинградского ун-та, 1982. 3. Елисеева И. И., Рукавишников В. О. Логика прикладного статистического анализа. - М.: Финансы и статистика, 1982. 4. Крастинь О. П. Разработка и интерпретация моделей корреляционных связей в экономике. - Рига: Занатне, 1983. 5. Кулаичев А. П. Методы и средства анализа данных в среде Windows. Stadia 6.0 - М.: НПО Информатика и компьютеры, 1996. 6. Статистическое моделирование и прогнозирование: Учебное пособие / Под ред. А. Г. Гранберга. - М.: Финансы и статистика, 1990. 7. Ферстер Э., Речи Б. Методы корреляционного и регрессионного анализа. Руководство для экономистов / Пер. с нем. - М.: Финансы и статистика, 1983. 8. Шураков В. В. и др. Автоматизированное рабочее место для статистической обработки данных. - М.: Финансы и статистика, 1990. | |



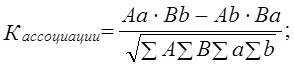 (8.48)
(8.48)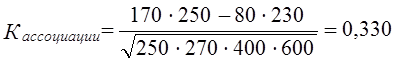
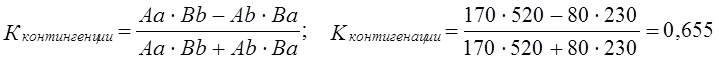
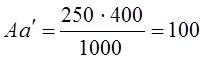 и
и 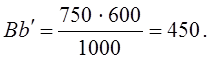
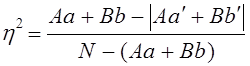 , (8.49)
, (8.49)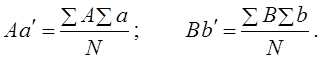
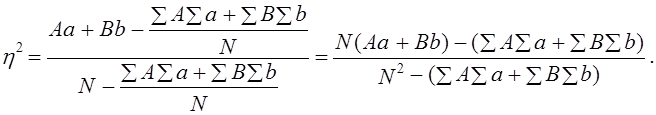 (8.50)
(8.50)