| Транспортная задача, в которой суммарные запасы и потребности совпадают, т. е. выполняется условие 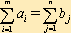 называется закрытой моделью; в противном случае – открытой. Для открытой модели может быть два случая: называется закрытой моделью; в противном случае – открытой. Для открытой модели может быть два случая:
а) суммарные запасы превышают суммарные потребности: 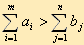 ; ;
б) суммарные потребности превышают суммарные запасы: 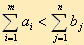 . .
Линейная функция одинакова в обоих случаях, изменяется только вид системы ограничений. Открытая модель ТЗ решается приведением к закрытой модели. В случае (а), когда суммарные запасы превышают суммарные потребности, т.е. 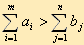 , вводится фиктивный потребитель (столбец Вn+1), потребности которого , вводится фиктивный потребитель (столбец Вn+1), потребности которого 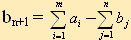 . В случае (б), когда суммарные потребности превышают суммарные запасы, т.е. . В случае (б), когда суммарные потребности превышают суммарные запасы, т.е. 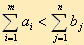 , вводится фиктивный поставщик (строка Am+1), запасы которого , вводится фиктивный поставщик (строка Am+1), запасы которого 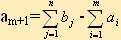 . . Стоимость перевозки единицы груза, как до фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика полагают равными нулю, так как груз в обоих случаях не перевозится.
После преобразований задача принимает вид закрытой модели и решается обычным способом. При равных стоимостях перевозки единицы груза, от поставщиков к фиктивному потребителю, затраты на перевозку груза реальным потребителям минимальны, а фиктивному потребителю будет направлен груз от наименее выгодных поставщиков. То же самое получаем и в отношении фиктивного поставщика. Замечание 1. Прежде чем решать какую-нибудь транспортную задачу, необходимо сначала проверять, к какой модели она принадлежит, и только после этого непосредственно составлять распределительную таблицу. Замечание 2. При составлении первоначального опорного плана методом минимальной стоимости или двойного предпочтения необходимо наименьшую стоимость выбирать только среди стоимостей реальных поставщиков и потребителей, а запасы фиктивного поставщика (потребности фиктивного потребителя) распределять в последнюю очередь. Это позволит получить план, более близкий к оптимальному.
Отмеченное во втором замечании используют также при введении фиктивно запятых клеток. Пример 2.8.1 Рекомендации приведения задачи к обычной ТЗ При решении конкретных транспортных задач приходится часто учитывать некоторые дополнительные ограничения: невозможность (запрет) поставки груза из Ak в Вi (блокировка), обеспечение пункта Вj , заданным количеством aij единиц груза за счет пункта отправления Ai и т.п. В этих случаях поступают следующим образом: Запрет перевозок груза из Ai в Вj осуществляется занесением в клетку Ai Вj числа cij = М > 0 (здесь и в последующем М - сколь угодно большое число). При оптимальном плане эта клетка будет блокирована. По условию задачи требуется доставить из Ai в Вj αij единиц груза. Следует занести в начале заполнения таблицы в клетку Ai Вj число αij , считать ее в дальнейшем свободной (cij = М), а потребности bj и запасы аi уменьшить на αij. Найденный оптимальный план новой задачи будет оптимальным и для исходной (с добавлением xij = αij ). Если требуется из Ai в Вj завести груз xij ≥ 0 - заданного числа, то уменьшают запасы аi и потребности bj на αij и находят оптимальный план новой задачи, по которому определяют и решение исходной задачи (x*ij = αij + xij, где xij > 0 - компонента плана новой задачи). Иногда требуется перевезти из Ai в Вj груза не более заданного объема xij < αij. Тогда, чаще всего, поступают следующим образом: в таблицу вводят дополнительный столбец В*j с тарифами, равными тарифам столбца Вj , кроме клетки Ai Вj , где полагаютcij = М. При этом потребности пункта Вj считаются равными αij , a В*j - равными bj - αij .
Находят решение полученной задачи обычными методами или устанавливают ее неразрешимость. Заметим, что исходная ТЗ разрешима лишь в том случае, когда для нее существует хотя бы один опорный план. Пример 2.8.2 Пример 2.8.3
| 
