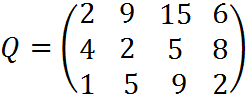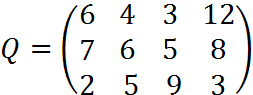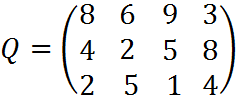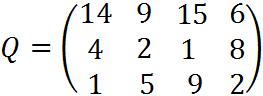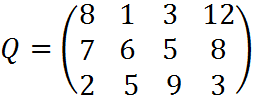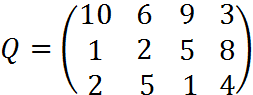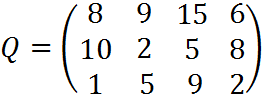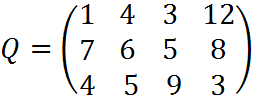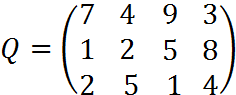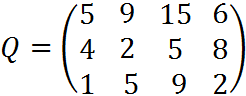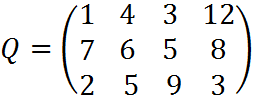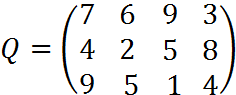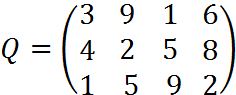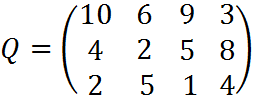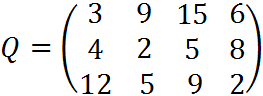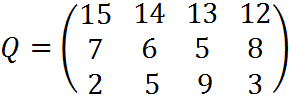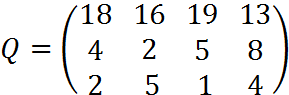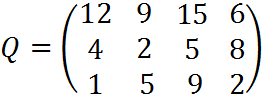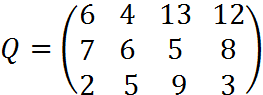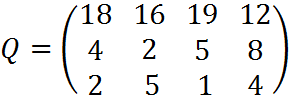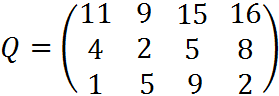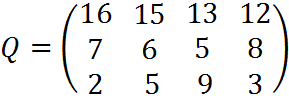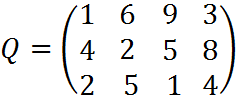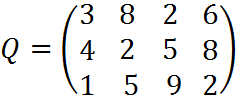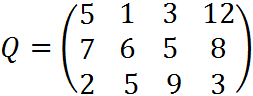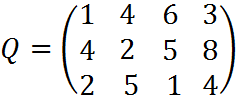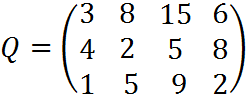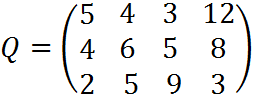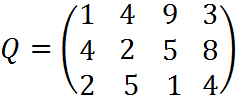Контрольная работа содержит 10 задач на темы:

1.Доходность и риск финансовой операции

2. Портфельный анализ

3. Облигации

Номер варианта соответствует последней цифре зачетной книжки (если последняя цифра 0, то номер варианта 10).

1 вариант

1.  Пусть доходности за два последовательных периода времени t₁  и  t₂  равны 10%  и 15 % соответственно. Определить доходность за период  t = t₁ + t_{2 .}

2. Доходность актива за месяц равна 3%.  Найти доходность актива за год  при условии, что месячная доходность в течение года постоянна.

3. Доходность актива за год  равна 24%.  Найдите доходность актива   за месяц, предполагая ее постоянство.

4. Пусть матрица последствий есть

Составить матрицу рисков.

5. Для матрицы  последствий

выберите вариант решения:

А) по критерию максимакса

Б) по критерию Вальда (максимина)

В)  по критерию Сэвиджа

В)  по критерию Гурвица при λ =1/2.

6. Для матрицы  последствий

известны вероятности развития реальной ситуации по каждому из четырех вариантов: p₁ =0,25,  p₂=0,35,  p₃=0,2,  p₄=0,2.

Выяснить:

1. при каком варианте решения достигается наибольший средний доход и какова величина этого дохода;

2. при каком варианте решения достигается наименьший средний ожидаемый риск, и найти величину минимального среднего ожидаемого риска (проигрыша);

3. Используя критерий Лапласа  выбрать наилучший вариант решения на основе правила максимизации среднего ожидаемого дохода.

7. Портфель состоит из трех видов акций (А, В и С), данные о которых приведены в таблице. Найти доходность портфеля.

8. В табл. приведены данные о доходности  двух бумаг за 5 лет

1) Определить значение ковариации для двух ценных бумаг А и Б.

2) Определить коэффициент корреляции между доходностями этих бумаг.

3) Определить риск портфеля, если доли ценных бумаг одинаковы.

9. Сформировать портфель минимального риска из двух видов ценных бумаг:

«А» с эффективностью14% и риском 20,

 и  «Б»  с эффективностью 6% и риском 7.

 При условии, что обеспечивается доходность портфеля не менее 10%.

Коэффициент корреляции равен 0.18.

10. Купонный доход 10-летней облигации номиналом 1500 руб. равен 15 %  годовых (выплаты в конце года). Найти средний срок поступления дохода от облигации.

2 вариант

1.  Пусть доходности за два последовательных периода времени t₁  и  t₂  равны 30%  и 10 % соответственно. Определить доходность за период  t = t₁ + t_{2 .}

2. Доходность актива за месяц равна 1,5%.  Найти доходность актива за год  при условии, что месячная доходность в течение года постоянна.

3. Доходность актива за год  равна 20%.  Найдите доходность актива   за месяц, предполагая ее постоянство.

4. Пусть матрица последствий есть

Составить матрицу рисков.

5. Для матрицы  последствий

выберите вариант решения:

А) по критерию максимакса

Б) по критерию Вальда (максимина)

В)  по критерию Сэвиджа

В)  по критерию Гурвица при λ =1/2.

6. Для матрицы  последствий

известны вероятности развития реальной ситуации по каждому из четырех вариантов: p₁ =0,25,  p₂=0,35,  p₃=0,1,  p₄=0,3.

Выяснить:

1. при каком варианте решения достигается наибольший средний доход и какова величина этого дохода;

2. при каком варианте решения достигается наименьший средний ожидаемый риск, и найти величину минимального среднего ожидаемого риска (проигрыша);

3. Используя критерий Лапласа  выбрать наилучший вариант решения на основе правила максимизации среднего ожидаемого дохода.

7. Портфель состоит из трех видов акций (А, В и С), данные о которых приведены в таблице. Найти доходность портфеля.

8. В табл. приведены данные о доходности  двух бумаг за 5 лет

1) Определить значение ковариации для двух ценных бумаг А и Б.

2) Определить коэффициент корреляции между доходностями этих бумаг.

3) Определить риск портфеля, если доли ценных бумаг одинаковы.

9. Сформировать портфель минимального риска из двух видов ценных бумаг:

«А» с эффективностью15% и риском 22,

 и  «Б»  с эффективностью 7% и риском 6.

 При условии, что обеспечивается доходность портфеля не менее 15%.

Коэффициент корреляции равен 0.3.

10. Купонный доход 8-летней облигации номиналом 2000 руб. равен 20 %  годовых (выплаты в конце года). Найти средний срок поступления дохода от облигации.

3 вариант

1.  Пусть доходности за два последовательных периода времени t₁  и  t₂  равны 20%  и 10 % соответственно. Определить доходность за период  t = t₁ + t_{2 .}

2. Доходность актива за месяц равна 2%.  Найти доходность актива за год  при условии, что месячная доходность в течение года постоянна.

3. Доходность актива за год  равна 30%.  Найдите доходность актива   за месяц, предполагая ее постоянство.

4. Пусть матрица последствий есть

Составить матрицу рисков.

5. Для матрицы  последствий

выберите вариант решения:

А) по критерию максимакса

Б) по критерию Вальда (максимина)

В)  по критерию Сэвиджа

В)  по критерию Гурвица при λ =1/2.

6. Для матрицы  последствий

известны вероятности развития реальной ситуации по каждому из четырех вариантов: p₁ =0,3,  p₂=0,35,  p₃=0,25,  p₄=0,1.

Выяснить:

1. при каком варианте решения достигается наибольший средний доход и какова величина этого дохода;

2. при каком варианте решения достигается наименьший средний ожидаемый риск, и найти величину минимального среднего ожидаемого риска (проигрыша);

3. Используя критерий Лапласа  выбрать наилучший вариант решения на основе правила максимизации среднего ожидаемого дохода.

7. Портфель состоит из трех видов акций (А, В и С), данные о которых приведены в таблице. Найти доходность портфеля.

8. В табл. приведены данные о доходности  двух бумаг за 5 лет

1) Определить значение ковариации для двух ценных бумаг А и Б.

2) Определить коэффициент корреляции между доходностями этих бумаг.

3) Определить риск портфеля, если доли ценных бумаг одинаковы.

9. Сформировать портфель минимального риска из двух видов ценных бумаг:

«А» с эффективностью11% и риском 18,

 и  «Б»  с эффективностью 6% и риском 7.

 При условии, что обеспечивается доходность портфеля не менее 12%.

Коэффициент корреляции равен 0.3.

10. Купонный доход 15-летней облигации номиналом 3000 руб. равен 10 %  годовых (выплаты в конце года). Найти средний срок поступления дохода от облигации.

4 вариант

1.  Пусть доходности за два последовательных периода времени t₁  и  t₂  равны 25%  и 35 % соответственно. Определить доходность за период  t = t₁ + t_{2 .}

2. Доходность актива за месяц равна 1%.  Найти доходность актива за год  при условии, что месячная доходность в течение года постоянна.

3. Доходность актива за год  равна 25%.  Найдите доходность актива   за месяц, предполагая ее постоянство.

4. Пусть матрица последствий есть

Составить матрицу рисков.

5. Для матрицы  последствий

выберите вариант решения:

А) по критерию максимакса

Б) по критерию Вальда (максимина)

В)  по критерию Сэвиджа

В)  по критерию Гурвица при λ =1/2.

6. Для матрицы  последствий

известны вероятности развития реальной ситуации по каждому из четырех вариантов: p₁ =0,15,  p₂=0,35,  p₃=0,2,  p₄=0,3.

Выяснить:

1. при каком варианте решения достигается наибольший средний доход и какова величина этого дохода;

2. при каком варианте решения достигается наименьший средний ожидаемый риск, и найти величину минимального среднего ожидаемого риска (проигрыша);

3. Используя критерий Лапласа  выбрать наилучший вариант решения на основе правила максимизации среднего ожидаемого дохода.

7. Портфель состоит из трех видов акций (А, В и С), данные о которых приведены в таблице. Найти доходность портфеля.

8. В табл. приведены данные о доходности  двух бумаг за 5 лет

1) Определить значение ковариации для двух ценных бумаг А и Б.

2) Определить коэффициент корреляции между доходностями этих бумаг.

3) Определить риск портфеля, если доли ценных бумаг одинаковы.

9. Сформировать портфель минимального риска из двух видов ценных бумаг:

«А» с эффективностью19% и риском 23,

 и  «Б»  с эффективностью 6% и риском 7.

При условии, что обеспечивается доходность портфеля не менее 15%.

Коэффициент корреляции равен 0.4

10. Купонный доход 15-летней облигации номиналом 5000 руб. равен 15 %  годовых (выплаты в конце года). Найти средний срок поступления дохода от облигации.

5 вариант

1.  Пусть доходности за два последовательных периода времени t₁  и  t₂  равны 12%  и 16 % соответственно. Определить доходность за период  t = t₁ + t_{2 .}

2. Доходность актива за месяц равна 2,5%.  Найти доходность актива за год  при условии, что месячная доходность в течение года постоянна.

3. Доходность актива за год  равна 25%.  Найдите доходность актива   за месяц, предполагая ее постоянство.

4. Пусть матрица последствий есть

Составить матрицу рисков.

5. Для матрицы  последствий

выберите вариант решения:

А) по критерию максимакса

Б) по критерию Вальда (максимина)

В)  по критерию Сэвиджа

В)  по критерию Гурвица при λ =1/2.

6. Для матрицы  последствий

известны вероятности развития реальной ситуации по каждому из четырех вариантов: p₁ =0,35,  p₂=0,35,  p₃=0,1,  p₄=0,2.

Выяснить:

1. при каком варианте решения достигается наибольший средний доход и какова величина этого дохода;

2. при каком варианте решения достигается наименьший средний ожидаемый риск, и найти величину минимального среднего ожидаемого риска (проигрыша);

3. Используя критерий Лапласа  выбрать наилучший вариант решения на основе правила максимизации среднего ожидаемого дохода.

7. Портфель состоит из трех видов акций (А, В и С), данные о которых приведены в таблице. Найти доходность портфеля.

8. В табл. приведены данные о доходности  двух бумаг за 5 лет

1) Определить значение ковариации для двух ценных бумаг А и Б.

2) Определить коэффициент корреляции между доходностями этих бумаг.

3) Определить риск портфеля, если доли ценных бумаг одинаковы.

9. Сформировать портфель минимального риска из двух видов ценных бумаг:

«А» с эффективностью15% и риском 21,

 и  «Б»  с эффективностью 6% и риском 7.

При условии, что обеспечивается доходность портфеля не менее 8%.

Коэффициент корреляции равен 0.4

10. Купонный доход 12-летней облигации номиналом 2500 руб. равен 14 %  годовых (выплаты в конце года). Найти средний срок поступления дохода от облигации.

6 вариант

1.  Пусть доходности за два последовательных периода времени t₁  и  t₂  равны 12%  и 14 % соответственно. Определить доходность за период  t = t₁ + t_{2 .}

2. Доходность актива за месяц равна 4%.  Найти доходность актива за год  при условии, что месячная доходность в течение года постоянна.

3. Доходность актива за год  равна 27%.  Найдите доходность актива   за месяц, предполагая ее постоянство.

4. Пусть матрица последствий есть

Составить матрицу рисков.

5. Для матрицы  последствий

выберите вариант решения:

А) по критерию максимакса

Б) по критерию Вальда (максимина)

В)  по критерию Сэвиджа

В)  по критерию Гурвица при λ =1/2.

6. Для матрицы  последствий

известны вероятности развития реальной ситуации по каждому из четырех вариантов: p₁ =0,25,  p₂=0,35,  p₃=0,2,  p₄=0,2.

Выяснить:

1. при каком варианте решения достигается наибольший средний доход и какова величина этого дохода;

2. при каком варианте решения достигается наименьший средний ожидаемый риск, и найти величину минимального среднего ожидаемого риска (проигрыша);

3. Используя критерий Лапласа  выбрать наилучший вариант решения на основе правила максимизации среднего ожидаемого дохода.

7. Портфель состоит из трех видов акций (А, В и С), данные о которых приведены в таблице. Найти доходность портфеля.

8. В табл. приведены данные о доходности  двух бумаг за 5 лет

1) Определить значение ковариации для двух ценных бумаг А и Б.

2) Определить коэффициент корреляции между доходностями этих бумаг.

3) Определить риск портфеля, если доли ценных бумаг одинаковы.

9. Сформировать портфель минимального риска из двух видов ценных бумаг:

«А» с эффективностью15% и риском 25,

 и  «Б»  с эффективностью 5% и риском 4.

При условии, что обеспечивается доходность портфеля не менее 10%.

Коэффициент корреляции равен 0.2

10. Купонный доход 7-летней облигации номиналом 1500 руб. равен 15 %  годовых (выплаты в конце года). Найти средний срок поступления дохода от облигации.

7 вариант

1.  Пусть доходности за два последовательных периода времени t₁  и  t₂  равны 20%  и 15 % соответственно. Определить доходность за период  t = t₁ + t_{2 .}

2. Доходность актива за месяц равна 1,2%.  Найти доходность актива за год  при условии, что месячная доходность в течение года постоянна.

3. Доходность актива за год  равна 28%.  Найдите доходность актива   за месяц, предполагая ее постоянство.

4. Пусть матрица последствий есть

Составить матрицу рисков.

5. Для матрицы  последствий

выберите вариант решения:

А) по критерию максимакса

Б) по критерию Вальда (максимина)

В)  по критерию Сэвиджа

В)  по критерию Гурвица при λ =1/2.

6. Для матрицы  последствий

известны вероятности развития реальной ситуации по каждому из четырех вариантов: p₁ =0,25,  p₂=0,35,  p₃=0,2,  p₄=0,2.

Выяснить:

1. при каком варианте решения достигается наибольший средний доход и какова величина этого дохода;

2. при каком варианте решения достигается наименьший средний ожидаемый риск, и найти величину минимального среднего ожидаемого риска (проигрыша);

3. Используя критерий Лапласа  выбрать наилучший вариант решения на основе правила максимизации среднего ожидаемого дохода.

7. Портфель состоит из трех видов акций (А, В и С), данные о которых приведены в таблице. Найти доходность портфеля.

8. В табл. приведены данные о доходности  двух бумаг за 5 лет

1) Определить значение ковариации для двух ценных бумаг А и Б.

2) Определить коэффициент корреляции между доходностями этих бумаг.

3) Определить риск портфеля, если доли ценных бумаг одинаковы.

9. Сформировать портфель минимального риска из двух видов ценных бумаг:

«А» с эффективностью14% и риском 22,

 и  «Б»  с эффективностью 7% и риском 8.

При условии, что обеспечивается доходность портфеля не менее 9%.

Коэффициент корреляции равен 0.3.

10. Купонный доход 9-летней облигации номиналом 1500 руб. равен 15 %  годовых (выплаты в конце года). Найти средний срок поступления дохода от облигации.

8 вариант

1.  Пусть доходности за два последовательных периода времени t₁  и  t₂  равны 10%  и 30 % соответственно. Определить доходность за период  t = t₁ + t_{2 .}

2. Доходность актива за месяц равна 2,5%.  Найти доходность актива за год  при условии, что месячная доходность в течение года постоянна.

3. Доходность актива за год  равна 32%.  Найдите доходность актива   за месяц, предполагая ее постоянство.

4. Пусть матрица последствий есть

Составить матрицу рисков.

5. Для матрицы  последствий

выберите вариант решения:

А) по критерию максимакса

Б) по критерию Вальда (максимина)

В)  по критерию Сэвиджа

В)  по критерию Гурвица при λ =1/2.

6. Для матрицы  последствий

известны вероятности развития реальной ситуации по каждому из четырех вариантов: p₁ =0,25,  p₂=0,3,  p₃=0,25,  p₄=0,2.

Выяснить:

1. при каком варианте решения достигается наибольший средний доход и какова величина этого дохода;

2. при каком варианте решения достигается наименьший средний ожидаемый риск, и найти величину минимального среднего ожидаемого риска (проигрыша);

3. Используя критерий Лапласа  выбрать наилучший вариант решения на основе правила максимизации среднего ожидаемого дохода.

7. Портфель состоит из трех видов акций (А, В и С), данные о которых приведены в таблице. Найти доходность портфеля.

8. В табл. приведены данные о доходности  двух бумаг за 5 лет

1) Определить значение ковариации для двух ценных бумаг А и Б.

2) Определить коэффициент корреляции между доходностями этих бумаг.

3) Определить риск портфеля, если доли ценных бумаг одинаковы.

9. Сформировать портфель минимального риска из двух видов ценных бумаг:

«А» с эффективностью12% и риском 18,

 и  «Б»  с эффективностью 6% и риском 7.

При условии, что обеспечивается доходность портфеля не менее 10%.

Коэффициент корреляции равен 0.15.

10. Купонный доход 10-летней облигации номиналом 1000 руб. равен 15 %  годовых (выплаты в конце года). Найти средний срок поступления дохода от облигации.

9 вариант

1.  Пусть доходности за два последовательных периода времени t₁  и  t₂  равны 30%  и 45 % соответственно. Определить доходность за период  t = t₁ + t_{2 .}

2. Доходность актива за месяц равна 3,5%.  Найти доходность актива за год  при условии, что месячная доходность в течение года постоянна.

3. Доходность актива за год  равна 25%.  Найдите доходность актива   за месяц, предполагая ее постоянство.

4. Пусть матрица последствий есть

Составить матрицу рисков.

5. Для матрицы  последствий

выберите вариант решения:

А) по критерию максимакса

Б) по критерию Вальда (максимина)

В)  по критерию Сэвиджа

В)  по критерию Гурвица при λ =1/2.

6. Для матрицы  последствий

известны вероятности развития реальной ситуации по каждому из четырех вариантов: p₁ =0,25,  p₂=0,35,  p₃=0,2,  p₄=0,2.

Выяснить:

1. при каком варианте решения достигается наибольший средний доход и какова величина этого дохода;

2. при каком варианте решения достигается наименьший средний ожидаемый риск, и найти величину минимального среднего ожидаемого риска (проигрыша);

3. Используя критерий Лапласа  выбрать наилучший вариант решения на основе правила максимизации среднего ожидаемого дохода.

7. Портфель состоит из трех видов акций (А, В и С), данные о которых приведены в таблице. Найти доходность портфеля.

8. В табл. приведены данные о доходности  двух бумаг за 5 лет

1) Определить значение ковариации для двух ценных бумаг А и Б.

2) Определить коэффициент корреляции между доходностями этих бумаг.

3) Определить риск портфеля, если доли ценных бумаг одинаковы.

9. Сформировать портфель минимального риска из двух видов ценных бумаг:

«А» с эффективностью16% и риском 23,

 и  «Б»  с эффективностью 9% и риском 7.

При условии, что обеспечивается доходность портфеля не менее 10%.

Коэффициент корреляции равен 0.5

10. Купонный доход 8-летней облигации номиналом 5000 руб. равен 12 %  годовых (выплаты в конце года). Найти средний срок поступления дохода от облигации.

10  вариант

1.  Пусть доходности за два последовательных периода времени t₁  и  t₂  равны 25%  и 30 % соответственно. Определить доходность за период  t = t₁ + t_{2 .}

2. Доходность актива за месяц равна 3,5%.  Найти доходность актива за год  при условии, что месячная доходность в течение года постоянна.

3. Доходность актива за год  равна 30%.  Найдите доходность актива   за месяц, предполагая ее постоянство.

4. Пусть матрица последствий есть

Составить матрицу рисков.

5. Для матрицы  последствий

выберите вариант решения:

А) по критерию максимакса

Б) по критерию Вальда (максимина)

В)  по критерию Сэвиджа

В)  по критерию Гурвица при λ =1/2.

6. Для матрицы  последствий

известны вероятности развития реальной ситуации по каждому из четырех вариантов: p₁ =0,25,  p₂=0,35,  p₃=0,2,  p₄=0,2.

Выяснить:

1. при каком варианте решения достигается наибольший средний доход и какова величина этого дохода;

2. при каком варианте решения достигается наименьший средний ожидаемый риск, и найти величину минимального среднего ожидаемого риска (проигрыша);

3. Используя критерий Лапласа  выбрать наилучший вариант решения на основе правила максимизации среднего ожидаемого дохода.

7. Портфель состоит из трех видов акций (А, В и С), данные о которых приведены в таблице. Найти доходность портфеля.

8. В табл. приведены данные о доходности  двух бумаг за 5 лет

1) Определить значение ковариации для двух ценных бумаг А и Б.

2) Определить коэффициент корреляции между доходностями этих бумаг.

3) Определить риск портфеля, если доли ценных бумаг одинаковы.

9. Сформировать портфель минимального риска из двух видов ценных бумаг:

«А» с эффективностью18% и риском 20,

 и  «Б»  с эффективностью 5% и риском 7.

При условии, что обеспечивается доходность портфеля не менее 10%.

Коэффициент корреляции равен 0.15.

10. Купонный доход 10-летней облигации номиналом 2000 руб. равен 20 %  годовых (выплаты в конце года). Найти средний срок поступления дохода от облигации.