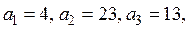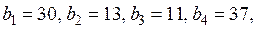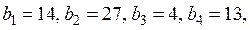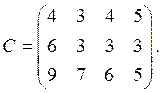| Общая информация » Каталог студенческих работ » ДРУГИЕ ЭКОНОМИЧЕСКИЕ ДИСЦИПЛИНЫ » Методы принятия управленческих решений |
| 16.10.2016, 11:07 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Студенты выполняют контрольную работу (20 вариантов). Номер варианта определяется по двум последним цифрам зачетной книжки: номер равен остатку от деления двух последних цифр на 20. Например, 138003 – вариант 3, 138024 – вариант 4, 138057 – вариант 17, 138030 – вариант 10, 138072 – вариант 12, 148040 – вариант 20, и т.д. Каждый из 20-ти вариантов контрольной работы содержит 3 задачи: Задача 1 – Составление математической модели задачи, Задача 2 – Графический метод нахождения оптимального решения, Задача 3 – Нахождение оптимального плана перевозок в транспортной задаче.
Задача 1. Составление математической модели экономической задачи Условия задач по вариантам (всего 20 вариантов) №1 Деталь некоторой машины изготовляют два цеховых участка. А и Б. производственные мощности этих участков описаны в таблице.
Составить математическую модель задачи выпуска наибольшего количества продукции при заданных объемах ресурсов. №2 Для производства двух видов продукции А и Б предприятие использует четыре группы оборудования. На производство единицы продукции А и Б требуется занять в течение смены 1, 0, 5, 2 ед. оборудования I, П, Ш, IV групп, а на производство единицы продукции Б требуется занять в течение смены 1, 1, 0, 2 ед. оборудования I, П, Ш, IV групп. В наличие имеется оборудования I группы – 18, П группы – 12, Ш группы – 24, IV группы – 18 единиц. Предприятие получает от реализации единицы продукции А 4 ден.ед. прибыли и 6 ден.ед. – для продукции Б. Сколько продукции каждого вида должно производить предприятие, чтобы получить наибольшую прибыль? Составить математическую модель задачи. №3 При производстве двух видов продукции А и Б используются три вида сырья. Составить план выпуска продукции, обеспечивающий максимум прибыли. Исходные данные:
Составить математическую модель задачи. №4 При производстве двух видов продукции А и Б используются три вида сырья. Составить план выпуска продукции, обеспечивающий максимум прибыли. Исходные данные:
Составить математическую модель задачи. №5 Для производства двух видов изделий А и В используется три вида сырья, имеющегося в количестве соответственно 8, 6, 12 кг. Нормы затрат каждого вида сырья на единицу продукции А и В и прибыль от реализации единицы продукции А, В приведены в таблице.
Найти план производства продукции, при котором доход предприятия от реализации всей продукции был наибольшим. Составить математическую модель задачи. №6 На станках Р1 и Р2 производится два вида продукции А и В. Для изготовления 1 ед. продукции А станок Р1 используется 2 часа, а станок Р2 - 1 часа. Для 1 ед. продукции В это время равно соответственно 2 часа и 3 часа. Продукции В должно быть произведено не более 4 ед. В течение суток станок Р1 может работать не более 16 часов, а станок Р2 - не более 18 часов. От реализации 1 ед. А прибыль составляет 2 ден. ед., а от 1 ед. В - 1 ден. ед. Какое количество продукции вида А и В нужно произвести, чтобы чистая прибыль была максимальной? Составить математическую модель задачи. №7 При производстве двух видов продукции А и Б используются три вида сырья. Составить план выпуска продукции, обеспечивающий максимум прибыли. Исходные данные:
Составить математическую модель задачи. №8 Обработка деталей А и В может производиться на трех станках. Причем каждая деталь при ее изготовлении должна последовательно обрабатываться на каждом из станков. Прибыль от реализации детали А – 100 ден. ед., детали В – 160 ден. ед. Исходные данные приведены в таблице.
Определить производственную программу, максимизирующую прибыль при условии: спрос на деталь А не менее 300 шт., на деталь В – не более 200 шт. Составить математическую модель задачи. №9 Предприятие располагает ресурсами двух видов в количестве 120 ед. и 80 ед. соответственно, которые используются для выпуска продукции А и Б. Расход на изготовление единицы продукции А составляет 2 ед. ресурса первого вида и 4 ед. ресурса второго вида, единицы продукции Б - 3 ед. ресурса первого вида и 1 ед. ресурса второго вида. Доход от реализации единицы продукции А составляет 6 ден. ед., вида Б - 4 ден. Известно, что продукции А должно быть выпущено не менее продукции вида Б. Нужно найти план выпуска продукции, обеспечивающий наибольшую прибыль. Составить математическую модель задачи. №10 Предприятие для выпуска продукции использует две технологии Т-1 и Т-2 (2 способа). Общее время работы предприятия по обеим технологиям Т= 500 ч. При этом необходимы три вида ресурсов. Известны запасы ресурсов, затраты ресурсов на 1 час работы с использованием каждой технологии, прибыль предприятия от реализации продукции, выпускаемой за 1 ч работы с использованием технологий (таблица).
Найти, сколько времени по каждой технологии должно работать предприятие, чтобы обеспечить максимум прибыли от реализации выпускаемой продукции. Составить математическую модель задачи. №11 Для производства столов и шкафов мебельная фабрика использует необходимые ресурсы. Нормы затрат ресурсов на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в следующей таблице:
Определить, сколько столов и шкафов фабрике следует изготовить, чтобы прибыль от их реализации была максимальной. Составить математическую модель задачи. №12 Фирма производит два продукта А и В, рынок сбыта которых неограничен. Каждый продукт должен быть обработан каждой из машин I, II, III. Время обработки в часах для каждого из изделий А и В приведено в таблице.
Время работы машины I, II, III соответственно 40, 36 и 36 ч в неделю. Прибыль от реализации одного изделия составляет соответственно 5 и 3 доллара. Фирме надо определить недельные нормы выпуска изделий А и В, максимизирующие прибыль. Составить математическую модель задачи. №13 Чаеразвесочная фабрика выпускает чай сортов А и Б, смешивая три ингредиента: индийский, цейлонский и английский чаи. В таблице приведены нормы расхода ингредиентов, объем запасов каждого ингредиента и прибыль от реализации 1 т чая сортов А и Б.
Требуется найти план производства чая сортов А и Б с целью получения наибольшей прибыли. Составить математическую модель задачи. №14 Для обеспечения перевозок нужно ежедневно формировать пассажирские и скорые поезда. В таблице указаны наличный парк вагонов разных типов, из которых комплектуются данные поезда, и количество пассажиров, вмещающихся в каждый из типов вагонов.
Определить число скорых и пассажирских поездов, при которых количество пассажиров достигает максимума. Составить математическую модель задачи. №15 Содержание витаминов А и С в 1 кг яблок и апельсин указано в таблице.
Известно, что 1 кг яблок стоит 60 руб., а 1 кг апельсинов 85 руб. Сколько яблок и апельсинов должен потреблять человек в сутки, чтобы получить не менее 75 мг витамина С и не менее 6 мг витамина А при наименьших затратах на яблоки и апельсины? Составить математическую модель задачи оптимального потребления яблок и апельсинов при заданных условиях. №16 Туристическая фирма в летний сезон обслуживает в среднем 7500 туристов в месяц и располагает флотилией из двух типов судов, характеристики которых представлены в таблице.
В месяц выделяется 60000 т горючего. Потребность в рабочей силе не превышает 600 чел. Определить количество судов I и II типа, чтобы обеспечить максимальный доход, который составляет от эксплуатации судов I типа 20 млн. руб., а II типа – 10 млн. руб. Составить математическую модель задачи оптимальной эксплуатации судов при заданных условиях. №17 Цех выпускает трансформаторы видов А и В. На один трансформатор вида А расходуется 5 кг трансформаторного железа и 3 кг проволоки, а на трансформатор вида В - 4 кг железа и 2 кг проволоки. От реализации трансформатора вида А прибыль составляет 12 ден. ед., вида В - 10 ден. ед. Сменный фонд железа - 480 кг, проволоки - 300 кг. Как следует спланировать выпуск трансформаторов, чтобы расход ресурсов не превышал выделенных фондов, а прибыль была наибольшей? Составить математическую модель задачи. №18 В суточный рацион включают два продукта питания П1 и П2, причем продукта П1 должно войти в дневной рацион не более 200 ед. Стоимость 1 ед. продукта П1 составляет 2 руб., продукта П2 – 4 руб. Содержание питательных веществ в 1 ед. продукта, минимальные нормы потребления указаны в таблице.
Определить оптимальный рацион питания, стоимость которого будет наименьшей. Составить математическую модель задачи. №19 Леспромхозу требуется не более 20 автомашин А и не более 15 автомашин В. Отпускная цена машины А 2 ден. ед., машины В - 4 ден. ед. ЛПХ может выделить для приобретения автомашин 50 ден. ед. Машина А грузоподъемности 3 т, машина В - 5 т. Сколько следует приобрести автомашин каждой марки, чтобы их общая грузоподъемность была наибольшей? Составить математическую модель задачи. №20 Для изготовления двух видов мебели А и Б используется 3 типа сырья, запасы которого и нормы расхода на единицу продукции заданы в таблице.
Определить план производства мебели, при котором прибыль максимальна. Составить математическую модель задачи.
Задача 2. Графический метод нахождения оптимального решения Дана задача линейного программирования
при ограничениях: Графическим методом найти оптимальные решения при стремлении целевой функции к максимальному и минимальному значениям. Значения коэффициентов в целевой функции
Задача 3. Нахождение оптимального плана перевозок в транспортной задачеУсловие задачи для всех вариантов: На заводах А1, A2, … производится однородная продукция в количестве a1, a2, … единиц. Потребителям В1, В2, В3, … требуется соответственно b1, b2, b3 … единиц готовой продукции. Известны расходы cij ден. ед. по перевозке единицы готовой продукции с завода Ai потребителю Bj. Необходимо найти план перевозок, минимизирующий общие затраты по изготовлению продукции на заводах и ее доставке потребителям. ЗАДАНИЕ 1. Внести числовые данные транспортной задачи в распределительную таблицу.
2. Составить математическую модель задачи. 3. Если транспортная задача открытого типа, то привести ее к закрытой. 4. Построить исходный план перевозок по методу «северо-западного угла» (Хс-з). Вычислить значение общих транспортных затрат для построенного плана. 5. Методом потенциалов проверить этот план X на оптимальность. 6. Если план не оптимальный, то последовательно улучшить его с помощью построения циклов пересчета в распределительной таблице. 7. Найти оптимальный план перевозок Хопт. 8. Определить по оптимальному плану перевозок Хопт: - количество продукции, отправляемое из каждого завода А1, A2 каждому потребителю В1, В2, В3; - наименьшие общие затраты на производство продукции и доставку ее потребителям; - заводы Аi, в которых остается нераспределенная продукция, и указать ее объем; - пункты потребления Вj, которые недополучают продукцию, и указать ее количество.
Задачи вариантов №№ 1–20 1.
................................. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

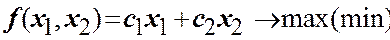 ,
,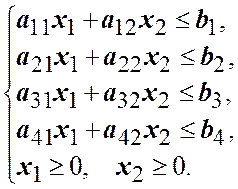
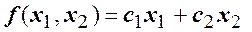 и в системе ограничений (всего 20 вариантов)
и в системе ограничений (всего 20 вариантов)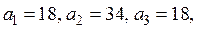 2.
2.