| Общая информация » Каталог студенческих работ » ГУМАНИТАРНЫЕ ДИСЦИПЛИНЫ » Логика |
| 15.11.2016, 15:33 | |
Выбор варианта производится по журналу. ВАРИАНТ №1 Задание № 1. Какие из следующих предложений являются высказываниями? Определите их истинность. 1. Наполеон был французским императором. 2. Чему равно расстояние от Земли до Марса? 3. Внимание! Посмотрите направо. 4. Электрон - элементарная частица. 5. Не нарушайте правил дорожного движения! Задание № 2. Определите значения логических переменных A, B, C, D, если: 1) А и (Париж - столица Франции) - истинное высказывание; 2) B и (Париж - столица Франции) - ложное высказывание; 3) C или (6 больше 10) - истинное высказывание; 4) D или (6 больше 10) - ложное высказывание. Задание № 3. Составить таблицы истинности для следующих логических выражений: Задание №4. Упростите логическую функцию: Задание № 5. Доказать формулу, составив таблицы истинности: a Ú (а Ù b) = a Ú b Задание № 6. Запишите логическую функцию, соответствующую функциональной схеме. Составьте таблицу истинности. Задание № 7. Нарисуйте функциональную схему для следующей логической функции: Задание № 8. Решите задачи: а) Трех друзей зовут Вова, Слава и Никита. Кто-то из них потерял солдатика. Их другу Егору сказали: 1. Солдатика потерял не Вова. 2. Солдатика потерял Слава. Но оказалось, что одно сообщение было ложным, а другое истинным. Кто потерял солдатика? б) В семье четверо детей – 5, 8, 13 и 15 лет. Их имена – Аня, Боря, Валя и Галя. Валя ходит в детский сад. Аня старше Бори. Сумма возрастов Ани и Вали делится на 3. Кому сколько лет? Задание № 9. Записать следующие высказывания в виде формул логики высказываний, используя пропозициональные (логические) переменные для обозначения элементарных высказываний, т.е. таких, которые уже не могут быть построены из каких-либо других высказываний: a) Пусть неверно, что если Джон – коммунист, то Джон – атеист; тогда Джон – коммунист или атеист, b) Необходимым, но не достаточным условием сходимости последовательности Задание № 10. а) Построить таблицу истинности для формулы. б) По полученной таблице истинности привести исходную формулу к дизъюнктивной нормальной форме. в) Упростить полученную в пункте б формулу, используя законы алгебры логики. г) Доказать с помощью тождественных преобразований равносильность упрощенной формулы (пункт в) и исходной (пункт а). д) Построить релейно-контактную схему, соответствующую упрощенной формуле (пункт в). е) Составить функциональные схемы на базе электронных логических элементов, реализующие логические функции из пунктах б и в. ж) найти СКНФ и СДНФ. Задание № 11. Разбить высказывание на элементарные и записать в виде кванторной формулы логики предикатов, используя наименьшее возможное число предикатов наименьшей местности; указать область определения использованных предикатов; привести формулу к предваренной нормальной форме: a) Либо каждый любит кого-то, и никто не любит всех, либо некто любит всех и кто-то не любит никого. b) Сумма любых двух чисел, имеющих различную четность, есть число нечетное. Задание № 12. Разработать алгоритм и построить его блок-схему для прикладной задачи с числом операторов–преобразователей не менее 7 и числом операторов-распознавателей (логических условий) не менее 4. Проверить разработанный алгоритм на выполнение свойств результативности, массовости и детерминированности. Варианты заданий (выбрать не менее двух задач для реализации): Посадка и проезд в поезде Посадка и проезд в общественном транспорте Управление автомобилем Приобретение компьютера Просмотр телепрограммы
ВАРИАНТ №2 Задание № 1. Какие из следующих предложений являются высказываниями? Определите их истинность. 1. Не все книги содержат полезную информацию. 2. Кошка является домашним животным. 3. Выразите 1 час 15 минут в минутах. 4. Ура! Каникулы! 5. Всякий моряк умеет плавать. Задание № 2. Определите значения логических переменных A, B, C, D, если: 1) A и (тигр - хищное животное) - истинное высказывание; 2) B и (тигр - хищное животное) - ложное высказывание; 3) C или (весна наступает после лета) - истинное высказывание; 4) D или (весна наступает после лета) ложное высказывание.
Задание № 3. Составить таблицы истинности для следующих логических выражений: Задание №4. Упростите логическую функцию: Задание № 5. Доказать формулу, составив таблицы истинности: (а Ù b) Ú (а Ù b) = b Задание № 6. Запишите логическую функцию, соответствующую функциональной схеме. Составьте таблицу истинности. Задание № 7. Нарисуйте функциональную схему для следующей логической функции: Задание № 8. Решите задачи: а) Три подруги – Аня, Лена и Даша – купили в магазине груши, яблоки и сливы. Каждая девочка покупала только один вид продуктов. Все покупки были разными. На вопрос о том, кто что купил, продавец ответил: «Аня купила груши. Лена купила не груши. Даша – не сливы». Как оказалось, только один из этих ответов был истинным. Что купили девочки? б) Эдика, Колю и Васю угостили печеньем 3-х сортов: с вареньем, с орехами и глазурью. Коля не любит орехи, Эдик не ест варенья, а Коля очень любит глазурь. Каждый ел печенье только одного сорта. Кто ел печенье с вареньем? Задание № 9. Записать следующие высказывания в виде формул логики высказываний, используя пропозициональные (логические) переменные для обозначения элементарных высказываний, т.е. таких, которые уже не могут быть построены из каких-либо других высказываний: a) Если мистер Джонс счастлив, то миссис Джонс несчастлива, и если мистер Джонс несчастлив, то миссис Джонс счастлива. b) Или Сэм пойдет на вечеринку, и Макс не пойдет на нее; или Сэм не пойдет на вечеринку, и Макс отлично проведет время. Задание № 10. а) Построить таблицу истинности для формулы. б) По полученной таблице истинности привести исходную формулу к дизъюнктивной нормальной форме. в) Упростить полученную в пункте б формулу, используя законы алгебры логики. г) Доказать с помощью тождественных преобразований равносильность упрощенной формулы (пункт в) и исходной (пункт а). д) Построить релейно-контактную схему, соответствующую упрощенной формуле (пункт в). е) Составить функциональные схемы на базе электронных логических элементов, реализующие логические функции из пунктах б и в. ж) найти СКНФ и СДНФ. Задание № 11. Разбить высказывание на элементарные и записать в виде кванторной формулы логики предикатов, используя наименьшее возможное число предикатов наименьшей местности; указать область определения использованных предикатов; привести формулу к предваренной нормальной форме: a) Всякий друг Мартина есть друг Джона, а Питер не есть друг Джона; следовательно, Питер не есть друг всякого друга Мартина. b) Если все рыбы, кроме акул, добры к детям, то найдутся дети, не любящие акул. Задание № 12. Разработать алгоритм и построить его блок-схему для прикладной задачи с числом операторов–преобразователей не менее 7 и числом операторов-распознавателей (логических условий) не менее 4. Проверить разработанный алгоритм на выполнение свойств результативности, массовости и детерминированности. Варианты заданий (выбрать не менее двух задач для реализации): Планирование отпуска Выполнение контрольной работы Пешеходная прогулка Посещение магазина Приобретение продуктов питания
ВАРИАНТ №3 Задание № 1. Какие из следующих предложений являются высказываниями? Определите их истинность. 1. Некоторые медведи - бурые. 2. Кто умеет плавать? 3. Киев - столица Украины. 4. Невозможно создать вечный двигатель. 5. Внимание! Проезд закрыт! Задание № 2. Определите значения логических переменных A, B, C, D, если: 1) A и (корова - домашнее животное) - истинное высказывание; 2) B и (корова - домашнее животное) - ложное высказывание; 3) C или (Земля - самая большая планета) - истинное высказывание; 4) D или (Земля - самая большая планета) - ложное высказывание. Задание № 3. Составить таблицы истинности для следующих логических выражений: Задание №4. Упростите логическую функцию: Задание № 5. Доказать формулу, составив таблицы истинности: а Ú а Ù b = а Ú b Задание № 6. Запишите логическую функцию, соответствующую функциональной схеме. Составьте таблицу истинности. Задание № 7. Нарисуйте функциональную схему для следующей логической функции: Задание № 8. Решите задачи: а) В замке три комнаты, в каждой из которых находится один из персонажей – либо принцесса, либо тигр, либо дракон. На двери каждой из комнат висит табличка с надписью. На первой двери написано: «Здесь находится принцесса или тигр». На второй написано: «Здесь находится тигр». На третьей написано: «Здесь находится дракон». Известно, что таблички на дверях комнат не соответствуют тому, что находится в комнатах. Определить, кто в какой комнате находится. б) Трех друзей зовут Дима, Витя и Женя. Найди, кто спрятал мишку, если известно, что все высказывания неверны. Дима: «Мишка у меня». Витя: «У Жени мишки нет». Женя: « Мишка у Вити». Задание № 9. Записать следующие высказывания в виде формул логики высказываний, используя пропозициональные (логические) переменные для обозначения элементарных высказываний, т.е. таких, которые уже не могут быть построены из каких-либо других высказываний: a) Неверно, что ни Петров, ни Сидоров не выдержали экзамен. b) Неверно, что если Иванов или Петров сдали экзамен, то и Сидоров его сдал. Задание № 10. а) Построить таблицу истинности для формулы. б) По полученной таблице истинности привести исходную формулу к дизъюнктивной нормальной форме. в) Упростить полученную в пункте б формулу, используя законы алгебры логики. г) Доказать с помощью тождественных преобразований равносильность упрощенной формулы (пункт в) и исходной (пункт а). д) Построить релейно-контактную схему, соответствующую упрощенной формуле (пункт в). е) Составить функциональные схемы на базе электронных логических элементов, реализующие логические функции из пунктах б и в. ж) найти СКНФ и СДНФ. Задание № 11. Разбить высказывание на элементарные и записать в виде кванторной формулы логики предикатов, используя наименьшее возможное число предикатов наименьшей местности; указать область определения использованных предикатов; привести формулу к предваренной нормальной форме: a) Если либо всякий любитель выпивки общителен, либо некий ростовщик честен и не пьет вина, то неверно, что всякий ростовщик общителен. b) Через любые три точки, не лежащие на одной прямой, проходит единственная плоскость. Задание № 12. Разработать алгоритм и построить его блок-схему для прикладной задачи с числом операторов–преобразователей не менее 7 и числом операторов-распознавателей (логических условий) не менее 4. Проверить разработанный алгоритм на выполнение свойств результативности, массовости и детерминированности. Варианты заданий (выбрать не менее двух задач для реализации): · Сортировка чисел по убыванию · Сортировка чисел по возрастанию · Планирование рабочего дня · Прохождение учебной сессии · Планирование учебного дня
ВАРИАНТ №4 Задание № 1. Какие из следующих предложений являются высказываниями? Определите их истинность. 1. Стой! Кто идет? 2. Человек все может. 3. Есть ли жизнь на Марсе? 4. Некоторые рыбы - хищники. 5. Ни один внимательный человек не совершит оплошность. Задание № 2. Определите значения логических переменных A, B, C, D, если: 1) A и (10<100) - истинное высказывание; 2) B и (10<100) - ложное высказывание; 3) C или (у прямоугольника все стороны равны) - истинное высказывание; 4) D или (у прямоугольника все стороны равны) - ложное высказывание. Задание № 3. Составить таблицы истинности для следующих логических выражений: Задание №4. Упростите логическую функцию: Задание № 5. Доказать формулу, составив таблицы истинности: а Ù (а Ú b) = а Ù b Задание № 6. Запишите логическую функцию, соответствующую функциональной схеме. Составьте таблицу истинности. Задание № 7. Нарисуйте функциональную схему для следующей логической функции: (X Ù (Y Ú X)) Ú ((Y Ú Z) Ù X) Задание № 8. Решите задачи: а) Четыре брата Коля, Володя, Петя и Юра – учатся в первом, втором, третьем и седьмом классах. Информатику в школе, в которой учатся мальчики, начинают изучать с седьмого класса. Петя учится только на «4» и «5», а младшие братья стараются брать с него пример. Володя уже изучает информатику. Юра помогает решать задачи младшему брату по математике. Кто из братьев учится во втором классе? б) Инопланетяне сообщили, что в их системе 3 планеты А, Б, В и что они живут на второй планете. Вдруг передатчик испортился и два сообщения: А – не третья, Б – не вторая, - оказались ложными. На какой планете живут разумные существа? Задание № 9. Записать следующие высказывания в виде формул логики высказываний, используя пропозициональные (логические) переменные для обозначения элементарных высказываний, т.е. таких, которые уже не могут быть построены из каких-либо других высказываний: a) Если в точке x функция f(x) достигает экстремума, то ее производная в этой точке либо равна нулю, либо не существует. b) Векторное поле является простейшим, если его дивергенция равна нулю, либо его ротор равен нулю, либо равны нулю и дивергенция, и ротор. Задание № 10. а) Построить таблицу истинности для формулы. б) По полученной таблице истинности привести исходную формулу к дизъюнктивной нормальной форме. в) Упростить полученную в пункте б формулу, используя законы алгебры логики. г) Доказать с помощью тождественных преобразований равносильность упрощенной формулы (пункт в) и исходной (пункт а). д) Построить релейно-контактную схему, соответствующую упрощенной формуле (пункт в). е) Составить функциональные схемы на базе электронных логических элементов, реализующие логические функции из пунктах б и в. ж) найти СКНФ и СДНФ. Задание № 11. Разбить высказывание на элементарные и записать в виде кванторной формулы логики предикатов, используя наименьшее возможное число предикатов наименьшей местности; указать область определения использованных предикатов; привести формулу к предваренной нормальной форме: a) Поскольку не все птицы могут летать, то есть птицы, не умеющие плавать. b) Если все школьники пошли в кино или в театр, то все школьники пошли в кино или некоторые школьники пошли в театр. Задание № 12. Разработать алгоритм и построить его блок-схему для прикладной задачи с числом операторов–преобразователей не менее 7 и числом операторов-распознавателей (логических условий) не менее 4. Проверить разработанный алгоритм на выполнение свойств результативности, массовости и детерминированности. Варианты заданий (выбрать не менее двух задач для реализации): Выбор и приобретение подарка Посещение больницы Разработка документа на компьютере Оформление командировки Ремонт помещения
ВАРИАНТ №5 Задание № 1. Какие из следующих предложений являются высказываниями? Определите их истинность. 1. Любой неразумный человек ходит на руках. 2. Все лекарства неприятны на вкус. 3. Будьте внимательны и осторожны! 4. Мой кот страшный забияка. 5. Кто там? Задание № 2. Определите значения логических переменных A, B, C, D, если: 1) A и (А - первая буква в алфавите) - истинное высказывание; 2) B и (А - первая буква в алфавите) - ложное высказывание; 3) C или (2+3=7) - истинное высказывание; 4) D или (2+3=7) - ложное высказывание. Задание № 3. Составить таблицы истинности для следующих логических выражений: Задание №4. Упростите логическую функцию: Задание № 5. Доказать формулу, составив таблицы истинности: аÚ(bÙc) = (аÚb)Ù(aÚc) Задание № 6. Запишите логическую функцию, соответствующую функциональной схеме. Составьте таблицу истинности. Задание № 7. Нарисуйте функциональную схему для следующей логической функции: Задание № 8. Решите задачи: а) Три друга – Алеша, Сережа и Денис – купили щенков разной породы – колли, ротвейлера и овчарку. Дали им клички Джек, Гриф и Шарик. Известно, что щенок Алеши темнее по окрасу, чем овчарка, Шарик и Джек. Щенок Сережи старше Джека, ротвейлера и овчарки. Определить, какой щенок у Дениса. б) Маша, Даша, Катя и Оля учатся в одной школе, но в разных классах: 7 «А», 7 «Б», 8 «А». Катя и Оля – одноклассницы. Маша и Катя учились в классах с одинаковой литерой. Маша и Даша были ученицами второго класса. Кто, в каком классе учился? Задание № 9. Записать следующие высказывания в виде формул логики высказываний, используя пропозициональные (логические) переменные для обозначения элементарных высказываний, т.е. таких, которые уже не могут быть построены из каких-либо других высказываний: a) Для того чтобы число было нечетным, достаточно, чтобы оно было простым, но не наоборот. b) Скалярное произведение двух векторов равно нулю тогда и только тогда, когда они перпендикулярны или хотя бы один из них равен нулю. Задание № 10. а) Построить таблицу истинности для формулы. б) По полученной таблице истинности привести исходную формулу к дизъюнктивной нормальной форме. в) Упростить полученную в пункте б формулу, используя законы алгебры логики. г) Доказать с помощью тождественных преобразований равносильность упрощенной формулы (пункт в) и исходной (пункт а). д) Построить релейно-контактную схему, соответствующую упрощенной формуле (пункт в). е) Составить функциональные схемы на базе электронных логических элементов, реализующие логические функции из пунктах б и в. ж) найти СКНФ и СДНФ. Задание № 11. Разбить высказывание на элементарные и записать в виде кванторной формулы логики предикатов, используя наименьшее возможное число предикатов наименьшей местности; указать область определения использованных предикатов; привести формулу к предваренной нормальной форме: a) Иногда встречаются люди с глазами разного цвета, значит, есть кареглазые люди или все люди голубоглазы или сероглазы. b) Не все кошки серы, поэтому все кошки не серые. Задание № 12. Разработать алгоритм и построить его блок-схему для прикладной задачи с числом операторов–преобразователей не менее 7 и числом операторов-распознавателей (логических условий) не менее 4. Проверить разработанный алгоритм на выполнение свойств результативности, массовости и детерминированности. Варианты заданий (выбрать не менее двух задач для реализации): Приобретение квартиры Продажа квартиры Работа проводника при посадке пассажиров Работа кассира по продаже железнодорожных билетов Работа инспектора ГИБДД | |

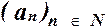 является ее ограниченность.
является ее ограниченность.