Задание №1

Решить графическим методом типовую задачу оптимизации. Составить двойственную к ней задачу.

В.1.

Инвестор, располагающий суммой в 300 тыс. ден. ед., может вложить свой капитал в акции автомобильного концерна А и строительного предприятия В. Чтобы уменьшить риск, акций А должно быть приобретено на сумму по крайней мере в два раза большую, чем акций В, причем последних можно купить не более чем на 100 тыс. ден. ед.

Дивиденды по акциям А составляют 8% в год, по акциям В — 10%. Какую максимальную прибыль можно получить в первый год?

Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если ре­шать задачу на минимум, и почему?

В.2.

Совхоз для кормления животных использует два вида корма. В дневном рационе животного должно содержаться не ме­нее 6 единиц питательного вещества A и не менее 12 единиц пита­тельного вещества В. Какое количество корма надо расходовать ежедневно на одно животное, чтобы затраты были минимальны­ми? Использовать данные таблицы.

Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если ре­шать задачу на максимум, и почему?

В.3.

Некоторая фирма выпускает два набора удобрений для газонов: обычный и улучшенный. В обычный набор входит 3 кг азотных, 4 кг фосфорных и 1 кг калийных удобрений, а в улучшен­ный — 2 кг азотных, 6 кг фосфорных и 3 кг калийных удобрений. Известно, что для некоторого газона требуется по меньшей мере 10 кг азотных, 20 кг фосфорных и 7 кг калийных удобрений. Обыч­ный набор стоит 3 ден. ед., а улучшенный — 4 ден. ед. Какие и сколько наборов удобрений нужно купить, чтобы обеспечить эф­фективное питание почвы и минимизировать стоимость?

Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если ре­шать задачу на максимум, и почему?

В.4.

На имеющихся у фермера 400 га земли он планирует по­сеять кукурузу и сою. Сев и уборка кукурузы требуют на каждый гектар 200 ден. ед. затрат, а сои — 100 ден. ед. На покрытие расхо­дов, связанных с севом и уборкой, фермер получил ссуду в 60 тыс. ден. ед. Каждый гектар, засеянный кукурузой, принесет 30 центне­ров, а каждый гектар, засеянный соей, — 60 центнеров. Фермер заключил договор на продажу, по которому каждый центнер куку­рузы принесет ему 3 ден. ед., а каждый центнер сои — 6 ден. ед. Однако согласно этому договору фермер обязан хранить убранное зерно в течение нескольких месяцев на складе, максимальная вместимость которого равна 21 тыс. центнеров.

Фермеру хотелось бы знать, сколько гектаров нужно засеять каждой из этих культур, чтобы получить максимальную прибыль.

Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если ре­шать задачу на минимум, и почему?

В.5.

Продукция двух видов (краска для внутренних (I) и на­ружных (Е) работ) поступает в оптовую продажу. Для производства красок используются два исходных продукта — А и В. Максималь­но возможные суточные запасы этих продуктов составляют 6 и 8 тонн соответственно. Расходы продуктов Л и В на 1 т соответству­ющих красок приведены в таблице.   

Изучение рынка сбыта показало, что суточный спрос на краску I никогда не превышает спроса на краску Е более чем на 1 т. Кроме того, установлено, что спрос на краску I никогда не превы­шает 2 т в сутки. Оптовые цены одной тонны красок равны 3000 ден. ед. для краски Е и 2000 ден. ед. для краски I. Какое коли­чество краски каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?

Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если ре­шать задачу на минимум, и почему?

В.6.

Финансовый консультант фирмы «АБС» консультирует клиента по оптимальному инвестиционному портфелю. Клиент хочет вложить средства (не более 25 ООО долл.) в два наименования акций крупных предприятий в составе холдинга «Дикси».

Анализируются акции «Дикси — Е» и «Дикси — В». Цены на ак­ции: «Дикси — Е» — 5 долл. за акцию; «Дикси — В» — 3 долл. за акцию.

Клиент уточнил, что он хочет приобрести максимум 6000 ак­ций обоих наименований, при этом акций одного из наименова­ний должно быть не более 5000 штук.

По оценкам «АБС», прибыль от инвестиций в эти акции в следующем году составит: «Дикси — Е» — 1,1 долл.; «Дикси -В» — 0,9 долл.

Задача консультанта состоит в том, чтобы выдать клиенту рекомендации по оптимизации прибыли от инвестиций.

Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если ре­шать задачу на минимум, и почему?

В.7.

Завод — производитель высокоточных элементов для автомобилей выпускает два различных типа деталей — Х и Y. Завод располагает фондом рабочего времени в 4000 чел.-ч в неделю. Для производства одной детали типа X требуется 1 чел.-ч, а для произ­водства одной детали типа Y— 2 чел.-ч. Производственные мощ­ности завода позволяют выпускать максимум 2250 деталей типа X и 1750 деталей типа У в неделю. Каждая деталь типа X требует 2 кг металлических стержней и 5 кг листового металла, а для производ­ства одной детали типа У необходимо 5 кг металлических стержней и 2 кг листового металла. Уровень запасов каждого вида металла составляет 10 000 кг в неделю. Кроме того, еженедельно завод по­ставляет 600 деталей типа X своему постоянному заказчику. Су­ществует также профсоюзное соглашение, в соответствии с кото­рым общее число производимых в течение одной недели деталей должно составлять не менее 1500 штук.

Сколько деталей каждого типа следует производить, чтобы максимизировать общий доход за неделю, если доход от производ­ства одной детали типа X составляет 30 ден. ед., а от производства одной детали типа У— 40 ден. ед.?

Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если ре­шать задачу на минимум, и почему?

В.8.

Имеется два вида корма I и II, содержащие питательные вещества (витамины) S₁, S₂ и S₃ Содержание числа единиц пита­тельных веществ в 1 кг каждого вида корма и необходимый мини­мум питательных веществ приведены в таблице.

Стоимость 1 кг корма I и II соответственно равна 4 и 6 ден. ед.

Необходимо составить дневной рацион, имеющий мини­мальную стоимость, в котором содержание питательных веществ каждого вида было бы не менее установленного предела.

Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если ре­шать задачу на максимум, и почему?

В.9.

При производстве двух видов продукции используется 4 типа ресурсов. Норма расхода ресурсов на производство едини­цы продукции, общий объем каждого ресурса заданы в таблице.

Прибыль от реализации одной единицы продукции первого вида составляет 2 ден. ед., второго вида — 3 ден. ед.

Задача состоит в формировании производственной про­граммы выпуска продукции, обеспечивающей максимальную прибыль от ее реализации.

Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если ре­шать задачу на минимум, и почему?

В.10.

Фирма производит два широко популярных безалко­гольных напитка — «Лимонад» и «Тоник». Фирма может продать всю продукцию, которая будет произведена. Однако объем произ­водства ограничен количеством основного ингредиента и произ­водственной мощностью имеющегося оборудования. Для произ­водства 1 л «Лимонада» требуется 0,02 ч работы оборудования, а для производства 1 л «Тоника» — 0,04 ч. Расход специального ингредиента составляет 0,01 кг и 0,04 кг на 1 л «Лимонада» и «То­ника» соответственно. Ежедневно в распоряжении фирмы имеется 24 ч времени работы оборудования и 16 кг специального ингреди­ента. Прибыль фирмы составляет 0,10 ден. ед. за 1 л «Лимонада» и 0,30 ден. ед. за 1 л «Тоника». Сколько продукции каждого вида следует производить ежедневно, если цель фирмы состоит в мак­симизации ежедневной прибыли?

Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если ре­шать задачу на минимум, и почему

Задание №2

а) Записать исходные данные задачи в виде транспортной таблицы, определить, открытой или закрытой является транспортная задача.

б) Сформулировать экономико-математическую модель ис­ходной транспортной задачи.

в) Найти оптимальный план перевозок, отметив при этом единственность или не единственность оптимального плана.

В1.

На строительном полигоне имеются три кирпичных завода, суточ­ные объемы производства которых соответственно равны 450 т, 350 т и 500 т кирпича. Эти заводы поставляют кирпич на четыре строитель­ных объекта, потребности в кирпиче которых в сутки составляют 300 т, 500 т, 350 т и 350 т соответственно. Стоимости перевозки одной тон­ны кирпича с первого завода на все объекты равны соответственно 1, 7, 5 и 2 ден. единиц; аналогичные стоимости перевозки со второго за­вода составляют 3, 1, 6 и 3 ден. единиц, а с третьего — 4, 3, 2 и 6 ден. единиц.

Составить оптимальный план перевозок кирпича с заводов на объек­ты, обеспечивающий минимальный затраты.

В2.

На складах А, В, С и Д находятся соответственно 50 т, 40 т, 40 т и 70 т муки, которую нужно доставить четырем хлебозаводам. Первому хлебозаводу требуется 50 т муки, второму — 40 т, третьему — 50 т и четвертому — 60 т муки. Стоимости доставки одной тонны муки со склада А каждому хлебозаводу соответственно равны 8, 3, 5 и 2 ден. единиц, со склада В — 7, 4, 9 и 8 ден. единиц, со склада С — 6, 3, 3 и 1 ден. единиц, со склада Д — 2, 4, 1 и 5 ден. единиц.

Составить план перевозки муки, обеспечивающий минимальные транспортные расходы.

В3.

Картофель из четырех районов должен быть перевезен в три храни­лища. Запасы картофеля в районах соответственно равны 400 т, 500 т, 800 т и 500 т. Возможности хранилищ соответственно равны 700 т, 800 т и 700 т. Затраты на перевозку одной тонны картофеля из перво­го района в каждое из хранилищ равны соответственно 1, 4 и 3 ден. единиц; аналогичные затраты на перевозку из второго района состав­ляют 7, 1 и 5 ден. единиц, из третьего — 4, 8 и 3 ден. единиц, из четвер­того — 6, 2 и 8 ден. единиц.

Найти план перевозок картофеля из райо­нов в хранилище, при котором транспортные расходы были бы мини­мальными.

В4.

На четырех складах фирмы находится 70, 30, 40 и 60 холодильников соответственно, которые следует доставить в четыре магазина фирмы в количестве 50, 70, 40 и 40 холодильников в каждый из магазинов.

Стоимости перевозки одного холодильника с первого склада в каж­дый из магазинов составляют 6, 4, 9 и 7 ден. единиц соответственно, со второго склада — 7,2, 5 и 6 ден. единиц, с третьего склада — 2, 6, 3 и 3 ден. единиц, с четвертого склада — 3, 3, 6 и 5 ден. единиц соответ­ственно.

Определить план перевозок холодильников со складов в ма­газины, при котором общие затраты на перевозку были бы наимень­шими.

В5.

Фирма на своих филиалах производит химические удобрения. На четырех складах фирмы хранится соответственно 20 т, 70 т, 110 т и 140 т необходимого сырья, а потребности в сырье трех филиалов фир­мы составляют 130 т, 80 т и 80 т сырья соответственно. Затраты на перевозку одной тонны сырья с первого склада на каждый из филиа­лов равны 3, 4 и 7 ден. единиц; соответствующие затраты для второго склада равны 1, 5 и 3 ден. единиц, для третьего склада — 7, 3 и 2 ден. единиц, а для четвертого склада — 4, 6 и 6 ден. единиц соответствен­но.

Составить оптимальный план перевозок сырья со складов на фили­алы, при котором транспортные затраты были бы минимальными.

В6.

Сталеплавильная компания располагает тремя заводами M1, М2, М3, производящими за некоторый период времени 50, 30 и 20 тыс. тонн стали. Свою продукцию компания поставляет четырем потребителям С1, С2, С3 и С4», потребности которых за тот же период времени состав­ляют 12, 15, 25 и 36 тыс. тонн. Стоимости перевозки 1 тыс. тонн стали с завода M1 потребителям C1, С2, С3 и С4 равны 15, 19, 19 и 15 ден. единиц соответственно; аналогичные стоимости перевоза с завода М2 равны 19, 18, 18 и 10 ден. единиц, а с завода М3 — 14, 16, 20 и 18 ден. единиц.

Определить оптимальный план перевозок, при котором общие затраты на перевозки являются минимальными.

В7.

Компания владеет тремя фабриками F1, F2 и F3, способными произ­вести еженедельно 50, 25 и 25 тыс. изделий соответственно. По дого­ворам компания поставляет продукцию четырем заказчикам C1, С2, С3 и С4, каждому из которых требуется 15, 20, 20 и 30 тыс. изделий ежене­дельно. Стоимости производства и транспортировки 1 тыс. изделий с фабрики F1 каждому из заказчиков составляют 13, 17, 17 и 14 ден. еди­ниц соответственно; аналогичные стоимости для фабрики F2 равны 18, 16, 16 и 18 ден. единиц, а для фабрики F3 — 12, 14, 19 и 17 ден. единиц.

Определить оптимальный план производства и транспортировки про­дукции, минимизирующий общие затраты компании.

В8.

Две фабрики F1 и F2 производят электронное оборудование, объемы выпуска которого за некоторый период для каждой фабрики составля­ют соответственно 16 и 12 тыс. изделий. Продукция фабрик поставля­ется трем потребителям C1, С2 и С3, которым за тот же период времени требуется 10, 13 и 7 тыс. изделий. Стоимости перевозок 1 тыс. изделий с фабрики F1 трем потребителям равны соответственно 5, 4 и 6 ден. единиц, а с фабрики F2 — 6, 3 и 2 ден. единицы.

Найти оптимальный план перевозки продукции с фабрики потребителям, при котором об­щие затраты на перевозку будут наименьшими.

В9.

Четыре сталелитейных завода Z1, Z2, Z3 и Z4 производят еженедель­но 950, 300, 1350 и 450 т стали соответственно. Потребителям А, В, С и D еженедельно нужно 250, 1000, 700 и 1100 от стали, а стоимости перевозок 1 т стали с заводов потребителям для завода ZI равны 12, 16, 21 и 19 ден. единиц, для завода Z2 — 4, 4, 9 и 5 ден. единиц, для завода Z3 — 3,8, 14 и 10 ден. единиц, а для завода Z4 — 24, 33, 36 и 34 ден. единиц соответственно.

Составить план транспортировки стали с заводов потребителям, чтобы минимизировать общую стоимость пе­ревозок.

В10.

Компания владеет тремя заводами А, В и С, объемы производства которых за некоторый период времени составляют 6 тыс., 3 тыс. и 3 тыс. единиц продукции. Компания поставляет продукцию в четыре города M1, М2, М3 и М4, которым требуется 1,5 тыс.; 2,5 тыс.; 2,7 тыс. и 3,3 тыс. единиц продукции соответственно. Стоимости транспортиров­ки единицы продукции с завода А в города M1, М2, М3 и М4 равны соответственно 1,4, 1 и 9 ден. единиц; аналогичные стоимости для завода В равны 9, 2, 2 и 8 ден. единиц, а для завода С — 6, 1, 7 и 3 ден. единицы соответственно.

Составьте оптимальный план перевозок про­дукции в города, минимизирующий общие затраты на перевозки.

Задание №3

После k лет эксплуатации промышленное оборудование может оказаться в одном из следующих состояний: 1) требуется незначительный ремонт; 2) необходимо заменить отдельные детали;  3) дальнейшая эксплуатация возможна лишь после капитального ремонта. Накопленный на предприятии опыт свидетельствует, что вероятности указанных состояний оборудования составляют соответственно p₁, p₂, p₃. В зависимости от сложившейся ситуации руководство предприятия может принять такие решения: 1) произвести ремонт своими силами, что потребует затрат, равных a₁₁, a₁₂, a₁₃ ед. в зависимости от состояния оборудования (в затраты включена стоимость ремонта и заменяемых деталей, убытки, связанные с ухудшением качества выпускаемой продукции, простоем неисправного оборудования); 2) произвести ремонт при помощи специалистов-ремонтников, что вызовет затраты, равные a₂₁, a₂₂, a₂₃ ед.; 3) заменить оборудование новым, на что будет израсходовано соответственно a₃₁, a₃₂, a₃₃ ед. Используя игровой подход, высказать рекомендации по оптимальному образу действий руководства предприятия.

В1.    p₁= 0,2, p₂= 0,7, p₃= 0,1.

a₁₁=3, a₁₂=7, a₁₃=11

a₂₁=9, a₂₂ =5, a₂₃=8

a₃₁=15, a₃₂=12, a₃₃=6

В2.    p₁= 0,3, p₂= 0,6, p₃= 0,1.

a₁₁=2, a₁₂=6, a₁₃=12

a₂₁=10, a₂₂ =4, a₂₃=9

a₃₁=14, a₃₂=13, a₃₃=8

В3.    p₁= 0,2, p₂= 0,6, p₃= 0,2.

a₁₁=4, a₁₂=7, a₁₃=10

a₂₁=8, a₂₂ =4, a₂₃=6

a₃₁=13, a₃₂=11, a₃₃=7

В4.    p₁= 0,3, p₂= 0,5, p₃= 0,2.

a₁₁=3, a₁₂=6, a₁₃=12

a₂₁=11, a₂₂ =6, a₂₃=9

a₃₁=15, a₃₂=14, a₃₃=8

В5.    p₁= 0,4, p₂= 0,5, p₃= 0,1.

a₁₁=2, a₁₂=8, a₁₃=12

a₂₁=10, a₂₂ =4, a₂₃=8

a₃₁=15, a₃₂=10, a₃₃=6

В6.    p₁= 0,2, p₂= 0,7, p₃= 0,1.

a₁₁=3, a₁₂=8, a₁₃=11

a₂₁=10, a₂₂ =4, a₂₃=8

a₃₁=16, a₃₂=10, a₃₃=6

В7.    p₁= 0,1, p₂= 0,8, p₃= 0,1.

a₁₁=2, a₁₂=7, a₁₃=10

a₂₁=8, a₂₂ =5, a₂₃=9

a₃₁=14, a₃₂=12, a₃₃=7

В8.    p₁= 0,3, p₂= 0,6, p₃= 0,1.

a₁₁=3, a₁₂=9, a₁₃=11

a₂₁=7, a₂₂ =5, a₂₃=10

a₃₁=132 a₃₂=9, a₃₃=5

В9.    p₁= 0,2, p₂= 0,6, p₃= 0,2.

a₁₁=4, a₁₂=8, a₁₃=11

a₂₁=10, a₂₂ =5, a₂₃=9

a₃₁=14, a₃₂=12, a₃₃=7

В10.    p₁= 0,3, p₂= 0,5, p₃= 0,2.

a₁₁=4, a₁₂=7, a₁₃=13

a₂₁=7, a₂₂ =4, a₂₃=10

a₃₁=13, a₃₂=11, a₃₃=6

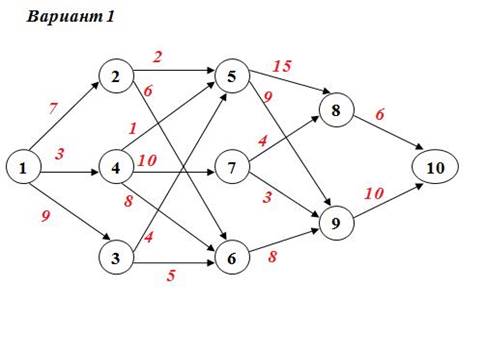
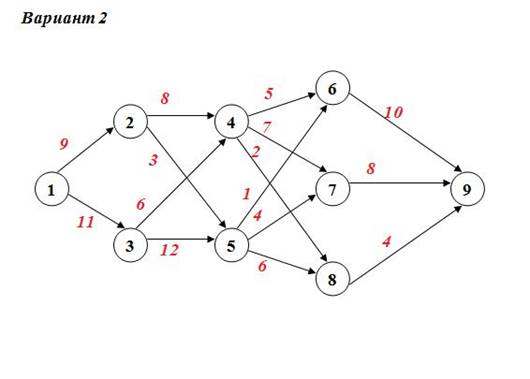
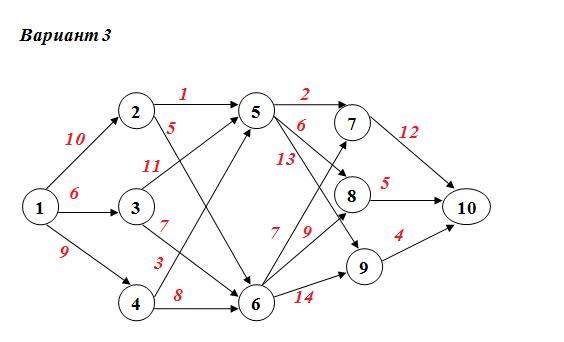
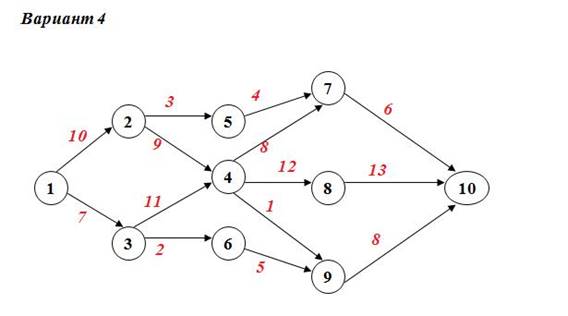
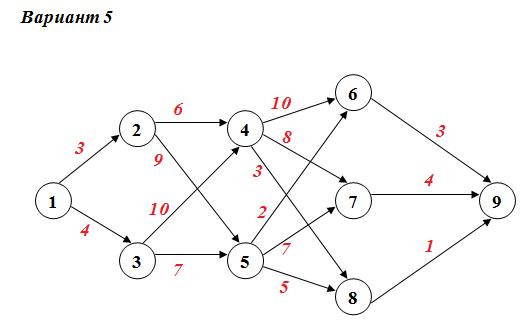
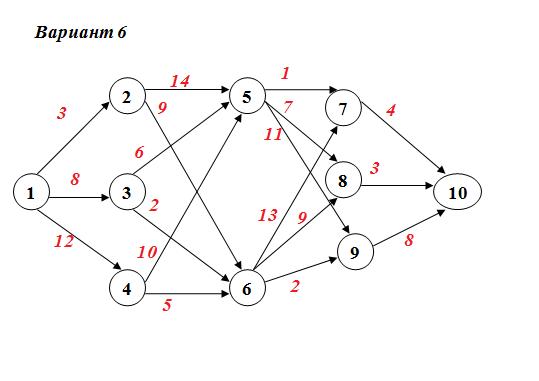
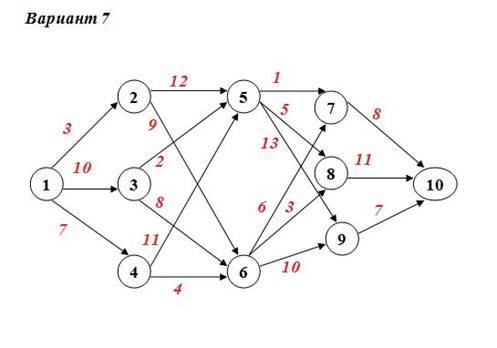
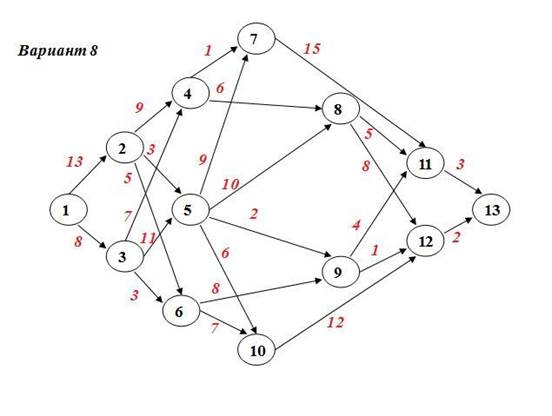
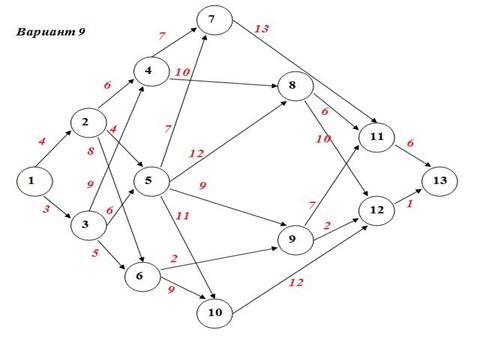
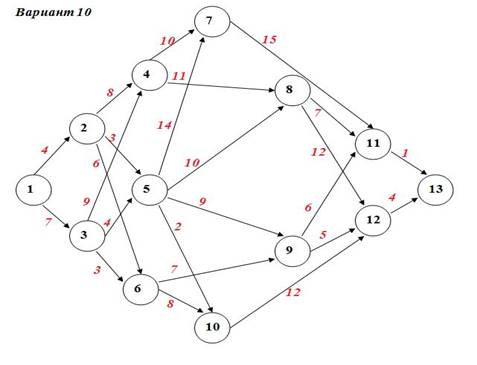
Задание №4

а) Для данной сети работ определить сроки свершения и резервы времени событий.

б) Найти критический путь для сети проекта.