| Общая информация » Каталог студенческих работ » СТАТИСТИКА » Статистика |
| 19.04.2014, 13:00 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ИНСТРУКЦИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОГО ЗАДАНИЯ Работа выполняется в Microsoft Word и оформляется в соответствии с требованиями к ПКЗ на ДО. Выбор варианта осуществляется по последней цифре номера зачетной книжки. Например. Номер Вашей зачетной книжки 9029. Последняя цифра 9, следовательно Вы выполняете все задания варианта № 9, номер зачетной книжки 10100 – выполняете все задания варианта № 0 и т. д. Задания выполняются в том порядке, в котором они приведены ниже. Вам необходимо выполнить по возможности максимальное количество заданий. Максимальное количество баллов за все задания — 100 баллов. Контрольная работа должна быть сдана за 1 - 2 недели до начала сессии (не позднее). Базовое пособие — Учебное пособие «Статистическая обработка данных». Для решения многих задач оказывается достаточно приложения Microsoft Office Excel. Основной навык, который требуется для решения математических задач с использованием Microsoft Office Excel, — это умение создавать формулы. В данной работе будут востребованы статистические функции. Можно найти среднее выборочное, сложив 100 чисел выборки и разделив результат на 100, а можно воспользоваться функцией СРЗНАЧ. А с помощью функции ЛИНЕЙН определить коэффициенты уравнения линейной регрессии. Мастер диаграмм позволяет легко получить графическое представление данных. Успеха в работе. Вариант 1 В таблице приведены сведения о заработной плате служащих одной фирмы
1. Построить по этим данным гистограмму. 2. Найти эмпирическую функцию распределения и построить ее график. 3. Вычислить среднее арифметическое выборки, выборочную дисперсию, выборочное среднее квадратичное отклонение, коэффициент вариации, размах вариации, начальные и центральные моменты до третьего порядка включительно, величину асимметрии и эксцесс, ошибки асимметрии и эксцесса. 4. Используя критерий Вариант 2 Наблюдения за жирностью молока дали такие результаты (%):
1. Построить по этим данным интервальный вариационный ряд случайной величины X с равными интервалами (первый интервал 3,45 - 3,55) и начертить гистограмму. 2. Найти эмпирическую функцию распределения и построить ее график. 3. Вычислить среднее арифметическое выборки, выборочную дисперсию, выборочное среднее квадратичное отклонение, коэффициент вариации, размах вариации, начальные и центральные моменты до третьего порядка включительно, величину асимметрии и эксцесс, ошибки асимметрии и эксцесса. 4. Используя критерии Вариант 3 Наблюдения за ошибкой взвешивания дали следующие результаты:
1. Построить по этим данным интервальный вариационный ряд случайной величины X с равными интервалами (первый интервал 0,020 - 0,024 и т.д.) и начертить гистограмму. 2. Найти эмпирическую функцию распределения и построить ее график. 3. Вычислить среднее арифметическое выборки, выборочную дисперсию, выборочное среднее квадратичное отклонение, коэффициент вариации, размах вариации, начальные и центральные моменты до третьего порядка включительно, величину асимметрии и эксцесс, ошибки асимметрии и эксцесса. 4. Используя критерии Вариант 4 Дана статистическая совокупность, характеризующая затраты (в копейках) на рубль продукции (работ, услуг) за 2003 г. по 100 предприятиям г. Н-ска:
1. Построить по этим данным интервальный вариационный ряд случайной величины X с равными интервалами (первый интервал 61,55 - 66,55 и т.д.) и начертить гистограмму. 2. Найти эмпирическую функцию распределения и построить ее график. 3. Вычислить среднее арифметическое выборки, выборочную дисперсию, выборочное среднее квадратичное отклонение, коэффициент вариации, размах вариации, начальные и центральные моменты до третьего порядка включительно, величину асимметрии и эксцесс, ошибки асимметрии и эксцесса. 4. Используя критерии Вариант 5 В течение месяца выборочно осуществлялась проверка торговых точек города по продаже овощей. В таблице представлены результаты проверки по недовесам покупателям одного вида овощей.
1. Построить по этим данным гистограмму. 2. Найти эмпирическую функцию распределения и построить ее график. 3. Вычислить среднее арифметическое выборки, выборочную дисперсию, выборочное среднее квадратичное отклонение, коэффициент вариации, размах вариации, начальные и центральные моменты до третьего порядка включительно, величину асимметрии и эксцесс, ошибки асимметрии и эксцесса. 4. Используя критерии Вариант 6 По результатам 80 пусков ракет определены расстояния (в км) до точек падения. Результаты оформлены в следующую статистическую совокупность:
1. Построить по этим данным интервальный вариационный ряд случайной величины X с равными интервалами (первый интервал 40,24 - 40,28 и т.д.) и начертить гистограмму. 2. Найти эмпирическую функцию распределения и построить ее график. 3. Вычислить среднее арифметическое выборки, выборочную дисперсию, выборочное среднее квадратичное отклонение, коэффициент вариации, размах вариации, начальные и центральные моменты до третьего порядка включительно, величину асимметрии и эксцесс, ошибки асимметрии и эксцесса. 4. Используя критерии Вариант 7 Дана статистическая совокупность, характеризующая продолжительность работы электроламп одного типа (в часах):
1. Построить по этим данным интервальный вариационный ряд случайной величины X с равными интервалами (первый интервал 8,4 - 10,4 и т.д.) и начертить гистограмму. 2. Найти эмпирическую функцию распределения и построить ее график. 3. Вычислить среднее арифметическое выборки, выборочную дисперсию, выборочное среднее квадратичное отклонение, коэффициент вариации, размах вариации, начальные и центральные моменты до третьего порядка включительно, величину асимметрии и эксцесс, ошибки асимметрии и эксцесса. 4. Используя критерии Вариант 8 Дана статистическая совокупность, характеризующая средний диаметр подшипников, обработанных на одном из станков завода:
1. Построить по этим данным интервальный вариационный ряд случайной величины X с равными интервалами (первый интервал 20,24 - 20,28 и т.д.) и начертить гистограмму. 2. Найти эмпирическую функцию распределения и построить ее график. 3. Вычислить среднее арифметическое выборки, выборочную дисперсию, выборочное среднее квадратичное отклонение, коэффициент вариации, размах вариации, начальные и центральные моменты до третьего порядка включительно, величину асимметрии и эксцесс, ошибки асимметрии и эксцесса. 4. Используя критерии Вариант 9 Дана статистическая совокупность, характеризующая длину нити в пряже (в метрах):
1. Построить по этим данным интервальный вариационный ряд случайной величины X с равными интервалами (первый интервал 51,55 - 56,55 и т.д.) и начертить гистограмму. 2. Найти эмпирическую функцию распределения и построить ее график. 3. Вычислить среднее арифметическое выборки, выборочную дисперсию, выборочное среднее квадратичное отклонение, коэффициент вариации, размах вариации, начальные и центральные моменты до третьего порядка включительно, величину асимметрии и эксцесс, ошибки асимметрии и эксцесса. 4. Используя критерии Вариант 0 В таблице приведено распределение квартир жилого дома по суточному потреблению электроэнергии (кВт.ч.). - Пирсона по данному вариационному ряду при уровне значимости
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
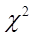- Пирсона по данным таблицы при уровне значимости 
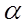=0,05, проверить гипотезу о том, что случайная величина X распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.