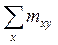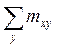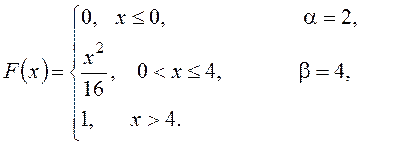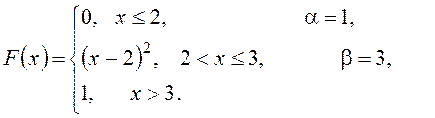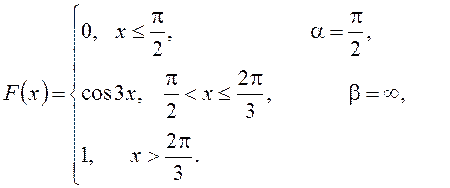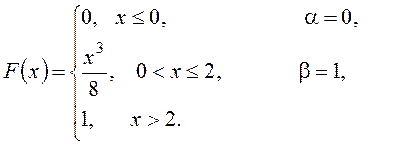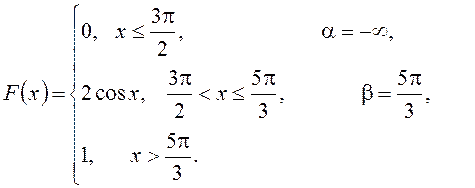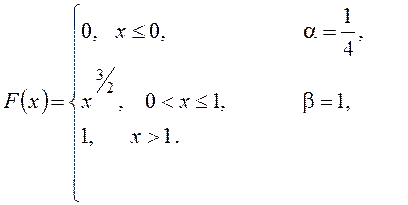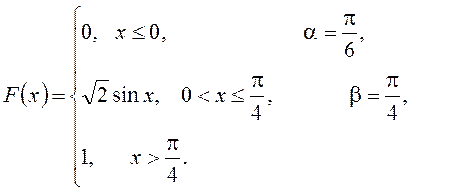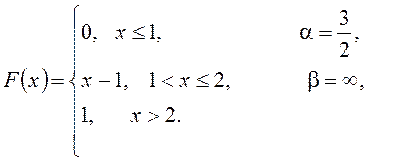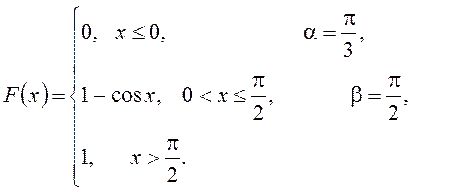Вариант №1.

1. Станок – автомат штампует детали. Вероятность, что изготовленная деталь бракованная равна 0,01. Найти вероятность того, что среди 200 деталей окажется:

а)  4 бракованных; б) более 165 небракованных.

в) Найти наиболее вероятное число бракованных деталей.

2. Среднее число вызовов, поступающих на АТС за 1 мин., равно двум. Найти вероятность того, что за 3 мин. поступит 7 вызовов.

3.  На складе находятся детали, изготовленные на двух заводах. Известно, что объем продукции первого завода  составляет 1/4, остальное – продукция второго завода. Вероятность брака на первом заводе равна 2%, на втором – 1%. Наудачу взятая деталь оказалась бракованной. Найти вероятность того, она изготовлена на втором заводе.

4. Наборщик пользуется двумя кассами (в одинаковой степени каждой). В первой кассе 90%, а во второй 80% отличного шрифта. Найти вероятность того, что наудачу извлеченная литера из наудачу взятой кассы будет отличного качества.

5. Монету бросают 5 раз. Найти вероятность того, что «герб» выпадет менее 2 раз.

6. Задана непрерывная случайная величина Χ функцией распределения F(х). Требуется: 1) найти плотность распределения вероятностей f(x) ; 2) схематично построить графики функций f(x) и F(х);3) найти  математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины Х; 4) найти вероятность того, что Х примет значение из интервала ().

7. Данные наблюдений над двумерной случайной величиной (Х; Y) представлены в корреляционной таблице. Найти выборочное уравнение прямой регрессии Y на X .

.

Вариант №2.

1. Работают 14 магазинов по продаже стиральных машин. Вероятность отказа покупателю в магазинах равна 0,1. Найти вероятность того, что покупатель получит отказ: а) в трех магазинах;  б) менее, чем в двух.

в) Найти наиболее вероятное число отказавших магазинов.

2. Среднее число заявок, поступивших на предприятие бытового обслуживания за 1 час, равно четырем. Найти вероятность того, что за 3 часа поступит 6 заявок.

3. В корзине 3 сорта яблок: 20 – первого, 15 – второго и 25 – третьего. Вероятность высокого содержания сахара в каждом из них соответственно равны 0,5, 0,6, 0,7. Наудачу взятое яблоко оказалось с высоким содержанием сахара. Найти, что это  яблоко 1 сорта.

4. На распределительной базе находятся электрические лампочки, изготовленные на двух заводах. Среди них 60% изготовлено первым заводом и 40% - вторым. Известно, что из которых 100 лампочек, изготовленных первым заводом, 95 удовлетворяют стандарту, а из 100 лампочек, изготовленных вторым заводом, удовлетворяют стандарту 85. Определить вероятность того, что взятая наудачу лампочка будет удовлетворять стандарту.

5. Студентка Петрова не очень добросовестно подготовилась к экзамену. Поэтому вероятность ответить на заданный ей вопрос равна 0,5. Какова вероятность того, что она ответит на три из семи заданных вопросов.

6.  Задана непрерывная случайная величина Χ функцией распределения F(х). Требуется: 1) найти плотность распределения вероятностей f(x) ; 2) схематично построить графики функций f(x) и F(х);
3) найти  математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины Х; 4) найти вероятность того, что Х примет значение из интервала ().

7. Данные наблюдений над двумерной случайной величиной (Х; Y) представлены в корреляционной таблице. Найти выборочное уравнение прямой регрессии Y на X.

.

Вариант №3.

1. На станциях отправления поездов находится 1000 автоматов для продажи билетов. Вероятность выхода из строя одного автомата в течение часа равна 0,005. Найти вероятность того, что в течение часа выйдут из строя:

а) 5 автоматов;  б) от 2 до 12 автоматов.

в) Найти наиболее вероятное число вышедших из строя автоматов.

2. Среднее число самолетов, прибывающих в аэропорт за 1 мин, равно трем. Найти вероятность того, что за 2 мин прибудут четыре самолета.

3. Два автомата по продаже газированной воды укомплектованы бумажными и пластмассовыми стаканами, причем первый содержит 20% бумажных стаканчиков, а второй 30%. Предложенная Вам газированная вода оказалась в пластмассовом стакане. Какова вероятность, что она набрана во втором автомате?

4. В мастерскую поступают телевизоры –75% от общего количества, стиральные машины - 15% и микроволновые печи – 10%. Вероятности того, что отремонтированный бытовой прибор прослужит в течение гарантийного срока, соответственно равны 0,9, 0,7 и 0,85. Найти вероятность того, что наудачу выбранный прибор сломался в гарантийное время.

5. Вероятность выиграть  по лотерейному билету равна 1/7. Найти вероятность выиграть не менее чем по двум билетам из шести.

6. Задана непрерывная случайная величина Χ функцией распределения F(х). Требуется: 1) найти плотность распределения вероятностей f(x) ; 2) схематично построить графики функций f(x) и F(х);
3) найти  математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины Х; 4) найти вероятность того, что Х примет значение из интервала ().

7.  Данные наблюдений над двумерной случайной величиной (Х; Y) представлены в корреляционной таблице. Найти выборочное уравнение прямой регрессии Y на X .

 .

Вариант №4.

1. Вероятность поражения мишени стрелком при одном выстреле 0,75. Найти вероятность того, что при 10 выстрелах стрелок поразит мишень:

а) 8 раз;  б) от 2 до 5 раз;  в) Найти наиболее вероятное число попаданий.

2. Среднее число кораблей, прибывающих в порт за 1 час, равно трем. Найти вероятность того, что за 4 часа прибудут в порт 6 кораблей.

3. Имеется три партии изделий, в каждой из которых содержится 3%, 2% и 1% некондиционных изделий соответственно. Из наугад выбранной партии случайным образом взятое изделие оказалось некондиционным. Какова вероятность того, что оно взято из первой партии?

4. На фабрике изготовляющей болты, первая машина производит 30%, вторая- 25%, третья – 45% всех изделий. Брак в их продукции составляет соответственно 2%, 1%, 3%. Найти вероятность того, что случайно выбранный болт окажется дефектным.

5. Монету подбрасывают 8 раз. Какова вероятность того, что она 6 раз упадет гербом вверх?

6. Задана непрерывная случайная величина Χ функцией распределения F(х). Требуется: 1) найти плотность распределения вероятностей f(x) ; 2) схематично построить графики функций f(x) и F(х);
3) найти  математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины Х; 4) найти вероятность того, что Х примет значение из интервала ().

7.  Данные наблюдений над двумерной случайной величиной (Х; Y) представлены в корреляционной таблице. Найти выборочное уравнение прямой регрессии Y на X .

.

Вариант №5.

1. Всхожесть семян огурцов равна 0,8. Найти вероятность того, что среди пяти посеянных семян взойдут:

а) не менее двух;  б) 4 семени;  в) Найти наиболее вероятное число взошедших семян.

2. Среднее число вызовов, поступающих на АТС за 1 мин., равно двум. Найти вероятность того, что за 4 мин. поступит 5 вызовов.

3. В библиотеке 90 учебников по математике разных лет издания: 25 - 1972г., 35 – 1983г и 30 – 1995г. Вероятности того, что учебники удовлетворяют программе соответственно равны 0,6, 0,7, 0,8. Наудачу взятый учебник соответствует программе. Найти вероятность того, что это учебник 1983 года.

4. Партия электрических лампочек на 20% изготовлена первым заводом, на 30% - вторым, на 50% - третьим. Вероятности выпуска бракованных лампочек соответственно равны q₁ =0,01, q₂ =0,005, q₃ =0,006. Найти вероятность того, что наудачу взятая из партии лампочка окажется стандартной.

5. Игральный кубик подбрасывается шесть раз подряд. Какова вероятность того, что шестерка выпадет ровно два раза?

6. Задана непрерывная случайная величина Χ функцией распределения F(х). Требуется: 1) найти плотность распределения вероятностей f(x) ; 2) схематично построить графики функций f(x) и F(х);
3) найти  математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины Х; 4) найти вероятность того, что Х примет значение из интервала ().

7.  Данные наблюдений над двумерной случайной величиной (Х; Y) представлены в корреляционной таблице. Найти выборочное уравнение прямой регрессии Y на X .

.

Вариант №6.

1. Вероятность выиграть в студенческой новогодней лотерее равна 0,3. Найти вероятность того, что среди 30 купленных студентом билетов окажется:

а) 10 выигрышных;  б) не более 9 выигрышных.

в) Найти наиболее вероятное число выигрышных билетов.

2. Среднее число заявок, поступивших на предприятие бытового обслуживания за 1 час, равно четырем. Найти вероятность того, что за 3 часа поступит 8 заявок.

3.  Два предприятия города хотели бы взять на временную работу студента. Вероятность того, что условия трудового договора устроят студента на первом предприятии, равна 0,7; на втором – 0,6. Студент с вероятностью в два раза большей может пойти на второе из данных предприятий, причем в течение одного рабочего дня  он может посетить только одно из них. В первый же день студент устроится на работу на одно из этих предприятий. Найти вероятность того, что он теперь работает на первом предприятии.

4. В продуктовом магазине в продаже имеется молочная продукция  двух молочно-консервных комбинатов: 40% продукции комбината А,  60% - комбината В. Вероятность некачественной продукции комбината А – 1%, комбината В – 2%. Найти вероятность того, что наудачу выбранный пакет молока окажется некачественным.

5. Вероятность того, что лотерейный билет окажется выигрышным, равна 0,3. Найти вероятность того, что два из четырех купленных гражданином билетов,  окажутся выигрышными.

6. Задана непрерывная случайная величина Χ функцией распределения F(х). Требуется: 1) найти плотность распределения вероятностей f(x) ; 2) схематично построить графики функций f(x) и F(х);
3) найти  математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины Х; 4) найти вероятность того, что Х примет значение из интервала ().

7.  Данные наблюдений над двумерной случайной величиной (Х; Y) представлены в корреляционной таблице. Найти выборочное уравнение прямой регрессии Y на X .

.

Вариант №7.

1. В новом микрорайоне построен новый дом, в котором 500 квартир. Вероятность продажи квартиры в доме равна 0,9. Найти вероятность того, что продано: а) 490 квартир;  б) от 200 до 350 квартир.

в) Найти наиболее вероятное число проданных квартир.

2. Среднее число самолетов, прибывающих в аэропорт за 1 мин, равно трем. Найти вероятность того, что за 3 мин прибудут четыре самолета.

3. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятности того, что деталь попадет к одному из них, соответственно равны 0,7 и 0,3. Вероятность того, что годная деталь будет признана стандартной первым контролером, равна 0,96, а вторым 0,78. Годная деталь при проверке была признана не стандартной. Найти вероятность того, что эту деталь проверил первый контролер.

4. Для экзаменационного сочинения по литературе может быть предложена одна из 6 тем по русской классической литературе или одна из 4 тем по современной литературе. Вероятность того, что ученик изложит на «отлично» тему по русской классике, равна 0,7, а по современной литературе – 0,4. Найти вероятность того, что ученик получит по сочинению «отлично». 

5. Монета брошена 7 раз. Какова вероятность того, что «герб» выпадет ровно три раза?

6. Задана непрерывная случайная величина Χ функцией распределения F(х).

Требуется:

1) найти плотность распределения вероятностей f(x);

2) схематично построить графики функций f(x) и F(х);
3) найти  математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины Х; 4) найти вероятность того, что Х примет значение из интервала ().

7.  Данные наблюдений над двумерной случайной величиной (Х; Y) представлены в корреляционной таблице. Найти выборочное уравнение прямой регрессии Y на X .

.

Вариант №8.

1. Всхожесть семян данного растения составляет 90%. Найти вероятность того, что из 700 семян взойдет: а) не менее 650;  б) 570 семян.

В) Найти наиболее вероятное число взошедших семян.

2. Среднее число кораблей, прибывающих в порт за 1 час, равно двум. Найти вероятность того, что за 4 часа прибудут в порт 6 кораблей.

3.  В обувной магазин поступает продукция двух фабрик по пошиву обуви: 40% с первой и 60% - со второй. Среди обуви, поступившей с первой фабрики 1% бракованной, а со второй – 3%. Купленная в этом магазине пара обуви оказалась бракованной. Какова вероятность того, что изготовлена эта пара  на второй фабрике?

4. Из пункта А в пункт В ведут две дороги: прямая и объездная. Вероятность проехать из А в В, не встретив заторов на перекрестках, по прямой дороге равна 0,3; по объездной – 0,9. Вероятность того, что водитель выберет прямую дорогу, равна 0,7; объездную – 0,3. Найти вероятность того, что на пути из А в В водитель не встретит «пробок» на дороге.

5.  Студент Иванов не очень добросовестно подготовился к экзамену. Поэтому вероятность ответить на заданный ему вопрос равна 0,5. Какова вероятность того, что он ответит на два из пяти заданных вопросов?

6. Задана непрерывная случайная величина Χ функцией распределения F(х). Требуется: 1) найти плотность распределения вероятностей f(x) ; 2) схематично построить графики функций f(x) и F(х);
3) найти  математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины Х; 4) найти вероятность того, что Х примет значение из интервала ().

7.  Данные наблюдений над двумерной случайной величиной (Х; Y) представлены в корреляционной таблице. Найти выборочное уравнение прямой регрессии Y на X .

.

Вариант №9.

1. В ралли принимают участие 500 экипажей, каждый из которых может сойти с дистанции из-за технических неполадок с вероятностью 0,05. Найти вероятность того, что среди них сойдут с дистанции:    а) от 4 до 8 экипажей;  б) 12 машин.

в) Найти наиболее вероятное число сошедших с дистанции экипажей.

2. Среднее число вызовов, поступающих на АТС за 1 мин., равно четырем. Найти вероятность того, что за 4 мин. поступит 7 вызовов.

3. С первого станка на сборку поступает 40%, со второго 60% всех деталей. Среди деталей, поступивших с первого станка 1% бракованных, со второго – 3%. Найти вероятность того, что поступившая на сборку бракованная деталь поступила с первого станка.

4. На двух автоматических станках изготовляются одинаковые детали. Известно, что производительность первого станка в два раза больше, чем второго, и что вероятность изготовления детали высшего качества на первом станке равна 0,9, а на втором - 0,81. Изготовленные за смену на обоих станках не рассортированные детали находятся на складе. Найти вероятность того, что наудачу взятая деталь окажется высшего качества.

5. Игральный кубик подбрасывается пять раз подряд. Какова вероятность того, что шестерка выпадет ровно три раза?

6. Задана непрерывная случайная величина Χ функцией распределения F(х). Требуется: 1) найти плотность распределения вероятностей f(x) ; 2) схематично построить графики функций f(x) и F(х);
3) найти  математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины Х; 4) найти вероятность того, что Х примет значение из интервала ().

7.  Данные наблюдений над двумерной случайной величиной (Х; Y) представлены в корреляционной таблице. Найти выборочное уравнение прямой регрессии Y на X .

.

Вариант №10.

1. Радиомастерская за год ремонтирует 730 магнитол. Вероятность неисправности в механической части отдельной магнитолы равна 0,2. Найти вероятность того, что среди них с указанной неисправностью за год окажется:

а) 550 магнитол;  б) от 110 до 370 магнитол.

в) Найти наиболее вероятное число магнитол с данной неисправностью.

2. Среднее число заявок, поступивших на предприятие бытового обслуживания за 1 час, равно пяти. Найти вероятность того, что за 3 часа поступит 3 заявки.

3. На предприятии работают две бригады рабочих: первая производит ¾ продукции с процентом брака 4%, вторая - ¼ продукции с процентом брака 6%. Найти вероятность того, что наугад взятое бракованное изделие изготовлено второй бригадой.

4. Два предприятия города хотели бы взять на временную работу студента. Вероятность того, что условия трудового договора устроят студента на первом предприятии, равна 0,8; на втором – 0,3. Студент с равной вероятностью может пойти на любое из  данных предприятий, причем в течение одного рабочего дня  он может посетить только одно из предприятий. Найти вероятность того, что в первый же день студент устроится на работу на одно из этих предприятий.

 5. Монета брошена 5 раз. Какова вероятность того, что «герб» выпадет ровно два раза?

6. Задана непрерывная случайная величина Χ функцией распределения F(х). Требуется: 1) найти плотность распределения вероятностей f(x) ; 2) схематично построить графики функций f(x) и F(х);
3) найти  математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины Х; 4) найти вероятность того, что Х примет значение из интервала ().

7.  Данные наблюдений над двумерной случайной величиной (Х; Y) представлены в корреляционной таблице. Найти выборочное уравнение прямой регрессии Y на X .

.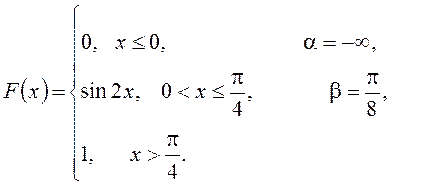
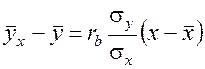