| Общая информация » Каталог студенческих работ » ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТ. СТАТИСТИКА » Теория вероятностей и мат. статистика |
| 13.10.2016, 19:57 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Экзаменационный/Зачетный билет № 1 1. Плотность вероятности и ее свойства. 2. Статистический критерий для сравнения двух дисперсий. 3. Игральная кость бросается 5 раз. Какова вероятность того, что двойка выпадет хотя бы один раз? 4. Вставить отсутствующее значение вероятности и найти M(x), D(x), s(x) случайной величины x:
Экзаменационный/Зачетный билет № 2 1. Случайные события. Алгебра событий. 2. Понятие о дисперсионном анализе. 3. В партии из 15 деталей имеются 10 стандартных. Наудачу отобраны 5 деталей. Найти вероятность того, что среди отобранных ровно 3 стандартных детали. 4.
Экзаменационный/Зачетный билет № 3 1. Нормальное распределение. 2. Полигон и гистограмма. Эмпирическая функция распределения и ее свойства. 3. Из колоды в 32 карты наугад вынимают 5. Найти вероятность того, что среди них окажется хотя бы один туз. 4. Случайная величина x имеет нормальное распределение с параметрами: а = 2, s = 1. Найти e, если R{|x - 2| < e} = 0,67.
Экзаменационный/Зачетный билет № 4 1. Теоремы сложения вероятностей. 2. Точечные оценки статистических параметров. Их свойства. Привести примеры. 3. В лаборатории имеются 6 калькуляторов и 4 компьютера. Вероятность безотказной работы калькулятора равна 0,95, а компьютера 0,8. Производится расчет наудачу в выбранном устройстве. Найти вероятность того, что во время расчета устройство не выйдет из строя. 4. Вставить отсутствующее значение вероятности и найти M(x), D(x), s(x) случайной величины x:
Экзаменационный/Зачетный билет № 5 1. Математическое ожидание, его свойства. 2. Статистический критерий для сравнения двух математических ожиданий. 3. Проводятся 6 независимых испытаний. Какова вероятность того, что событие А появится не менее, чем в двух и не более, чем в четырех испытаниях, если вероятность появления события А в каждом испытании равна 0,9? 4.
Экзаменационный/Зачетный билет № 6 1. Корреляционный момент и коэффициент корреляции. Его свойства. 2. Статистический критерий согласия Пирсона. 3. Из колоды в 32 карты вынимают сразу 3 карты. Найти вероятность того, что эти карты будут дамой, семеркой и тузом. 4. Случайная величина x имеет нормальное распределение с параметрами: а = 4, s = 0,8. Найти R{3 < x < 5}.
Экзаменационный/Зачетный билет № 7 1. Коэффициент корреляции. Уравнение прямой регрессии. 2. Основные понятия теории статистической проверки гипотез. 3. Колода в 12 карт (6 красных и 6 черных) делится пополам. Найти вероятность того, что число красных и черных карт в обеих пачках будет одинаковым. 4. Вставить отсутствующее значение вероятности и найти M(x), D(x), s(x) случайной величины x:
Экзаменационный/Зачетный билет № 8 1. Дисперсия, ее свойства. 2. Выборочный коэффициент корреляции. Выборочное уравнение прямой регрессии. 3. Два автомата производят детали, которые поступают на общий конвейер. Вероятность получения бракованной детали на первом автомате равна 0,05, на втором 0,06. Производительность второго автомата вдвое больше производительности первого. Найти вероятность того, что наудачу взятая с конвейера деталь небракованная. 4.
Экзаменационный/Зачетный билет № 9 1. Теоремы умножения вероятностей. Условные вероятности. 2. Выборочный коэффициент корреляции. Выборочное уравнение прямой регрессии. 3. Прибор состоит из трех последовательно соединенных блоков. Отказ прибора наступает в случае отказа хотя бы одного блока. Блоки отказывают независимо, вероятность отказа первого блока равна 0,1, второго 0,2, третьего 0,5. Найти вероятность того, что прибор исправен. 4. Случайная величина x имеет нормальное распределение с параметрами: а = 3, s = 1. Найти R{2 < x < 4}.
Экзаменационный/Зачетный билет № 10 1. Формула полной вероятности. Формула Бейеса. 2. Выборочная средняя и дисперсия. Их свойства. 3. В ящике среди 100 деталей находится одна бракованная. Из ящика наудачу извлечены 10 деталей. Найти вероятность того, что среди них окажется бракованная. 4. Вставить отсутствующее значение вероятности и найти M(x), D(x), s(x) случайной величины x:
Экзаменационный/Зачетный билет № 11 1. Уравнения прямой регрессии. 2. Однофакторный дисперсионный анализ. 3. В коробке 5 одинаковых изделий, причем 3 из них окрашены. Наудачу извлечены 2 изделия. Найти вероятность того, что среди двух извлеченных изделий окажется хотя бы одно окрашенное изделие. 4.
Экзаменационный/Зачетный билет № 12 1. Повторение испытаний. Формула Бернулли. 2. Генеральная и выборочная дисперсии. Их свойства. 3. Два станка производят детали, поступающие на общий конвейер. Вероятность брака на первом станке равна 0,04, на втором 0,06. Производительность первого станка втрое больше производительности второго. Найти вероятность того, что наудачу взятая с конвейера деталь небракованная. 4. Случайная величина x имеет нормальное распределение с параметрами: а = 1, s = 3. Найти R{|x – 1| < 2}.
Экзаменационный/Зачетный билет № 13 1. Неравенство Чебышева. Закон больших чисел в форме Чебышева. 2. Выборочный коэффициент корреляции. Выборочное уравнение прямой регрессии. 3. Проводятся 5 независимых испытаний. Какова вероятность того, что событие А появится не менее, чем в двух испытаниях, если вероятность появления события А в каждом испытании равна 0,9? 4.
Экзаменационный/Зачетный билет № 14 1. Неравенство Чебышева. Закон больших чисел в форме Бернулли. 2. Доверительные интервалы для математического ожидания. 3. Из колоды в 32 карты наугад вынимают 5. Найти вероятность того, что среди них окажется хотя бы один туз. 4. Случайная величина x имеет нормальное распределение с параметрами: а = 4, s = 0,8. Найти R{3 < x < 5}.
Экзаменационный/Зачетный билет № 15 1. Функция распределения случайной величины. Ее свойства для дискретной и непрерывной случайной величины. 2. Статистические критерии для сравнения математического ожидания и вероятности с заданным значением. 3. В коробке 5 одинаковых изделий, причем 3 из них окрашены. Наудачу извлечены 2 изделия. Найти вероятность того, что среди двух извлеченных изделий окажется хотя бы одно окрашенное изделие. 4.
Экзаменационный/Зачетный билет № 16 1. Плотность распределения случайной величины. Ее свойства. 2. Проверка гипотезы о значимости выборочного коэффициента корреляции. 3. Прибор состоит из трех последовательно соединенных блоков. Отказ прибора наступает в случае отказа хотя бы одного блока. Блоки отказывают независимо, вероятность отказа первого блока равна 0,1, второго 0,2, третьего 0,5. Найти вероятность того, что прибор исправен. 4. Вставить отсутствующее значение вероятности и найти M(x), D(x), s(x) случайной величины x:
Экзаменационный/Зачетный билет № 17 1. Примеры законов распределения дискретных случайных величин, их моменты. 2. Доверительные интервалы для математического ожидания. 3. Два станка производят детали, поступающие на общий конвейер. Вероятность брака на первом станке равна 0,04, на втором 0,06. Производительность первого станка втрое больше производительности второго. Найти вероятность того, что наудачу взятая с конвейера деталь небракованная. 4.
Экзаменационный/Зачетный билет № 18 1. Закон нормального распределения вероятностей и его моменты. Функция Лапласа. 2. Доверительные интервалы для дисперсии. 3. При изготовлении детали заготовка должна пройти 3 операции. Предполагая появление брака на отдельных операциях событиями независимыми, найти вероятность изготовления стандартной детали, если вероятность брака на первой операции равна 0,02, на второй 0,01, на третьей 0,03. 4. Случайная величина x имеет нормальное распределение с параметрами: а = 1, s = 3. Найти R{|x – 1| < 2}.
Экзаменационный/Зачетный билет № 19 1. Закон равномерного распределения вероятностей и его моменты. 2. Статистические оценки математического ожидания и корреляционной функции случайного процесса. 3. Проводятся 5 независимых испытаний. Какова вероятность того, что событие А появится не менее, чем в двух испытаниях, если вероятность появления события А в каждом испытании равна 0,9? 4. Вставить отсутствующее значение вероятности и найти M(x), D(x), s(x) случайной величины x:
Экзаменационный/Зачетный билет № 20 1. Стационарные случайные процессы. Спектральная плотность. Белый шум. 2. Точечные оценки статистических параметров. Их свойства. Привести примеры. 3. В лаборатории имеются 6 калькуляторов и 4 компьютера. Вероятность безотказной работы калькулятора равна 0,95, а компьютера 0,8. Производится расчет наудачу в выбранном устройстве. Найти вероятность того, что во время расчета устройство не выйдет из строя. 4.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

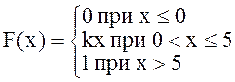 . Найти j(х), k, М(x), D(x). Построить графики j(х), F(х).
. Найти j(х), k, М(x), D(x). Построить графики j(х), F(х).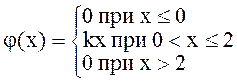 . Найти k, F(x), М(x), D(x). Построить графики j(х), F(х).
. Найти k, F(x), М(x), D(x). Построить графики j(х), F(х).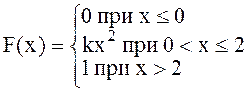 . Найти j(х), k, М(x), D(x). Построить графики j(х), F(х).
. Найти j(х), k, М(x), D(x). Построить графики j(х), F(х).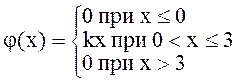 . Найти k, F(x), М(x), D(x). Построить графики j(х), F(х).
. Найти k, F(x), М(x), D(x). Построить графики j(х), F(х).