| Общая информация » Каталог студенческих работ » ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТ. СТАТИСТИКА » Теория вероятностей и мат. статистика |
| 26.04.2016, 10:04 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Номер варианта, который должен выполнять студент, соответствует последней цифре номера студенческого билета (или зачетной книжки). Контрольные задания 1. Классическое определение вероятности. 1.1. Из слова «наугад» выбирается случайно одна буква. Какова вероятность, что эта буква «а»? Какова вероятность того, что это гласная? 1.2. Брошены 3 монеты. Найти вероятность того, что выпадут два герба? 1.3. В бригаде работают 6 мужчин и 4 женщины. Для производства работ в соседний цех откомандировали 5-х. Какова вероятность, что среди них 2 мужчин и 3 женщины? 1.4. Брошены два игральных кубика. Какова вероятность, что в сумме выпадет 7 очков? 1.5. Какова вероятность того, что случайно сложив в ряд 5 карточек, на которых написаны буквы А, Г, И, К, и Н, прочитаем слово "КНИГА"? 1.6. Партия из 10 деталей содержит 7 стандартных и 3 нестандартных детали. Для контроля отбираются две. Какова вероятность, что обе детали стандартные? 1.7. Человек забыл последнюю цифру почтового индекса. Какова вероятность того, что, написав ее наугад, он получит верный индекс? 1.8. Случайным образом выбирается двузначное число. Найти вероятность того, что оно делится либо на 2, либо на 5. 1.9. Найти вероятность того, что при подбрасывании игральной кости один раз выпадает шесть очков; не менее трех очков; четное число очков ? 1.10. На пяти карточках написаны буквы А, А, Б, Н и Н. Случайным образом карточки выложены в ряд. Какова вероятность того, что сложилось слово "банан"?
2. Теоремы сложения и умножения вероятностей 2.1. В цепь последовательно включены три независимо работающих элемента с вероятностями отказа соответственно 0,1; 0,15 и 0,2. Какова вероятность того, что по цепи ток не идет? 2.2. Одновременно подбрасывают монету и игральную кость. Если на монете выпал герб, то выигрыш составляет 0 очков, а если решка - 2 очка. Эти очки суммируются с очками на кубике. Найти вероятность того, что суммарный выигрыш на кости и монете составит четыре очка. 2.3. Вероятность того, что можно выбить 10 очков на данной дистанции для данного стрелка при одном выстреле, равна 0,1, девять очков – 0,3. Какова вероятность того, что при трех выстрелах будет выбито более 27 очков? 2.4. Вероятность выигрыша на один билет 0,13. Какова вероятность хотя бы одного выигрыша для владельца пяти билетов 2.5.Три стрелка произвели залп, причем две пули поразили мишень. Найти вероятность того, что третий стрелок поразил мишень, если вероятности попадания первым, вторым и третьим стрелком равны соответственно 0,6; 0,5 и 0,4. 2.6. На склад поступает 60% продукции с первого участка и 40% со второго, причем с первого – 80% изделий первого сорта, а со второго – 75%. Какова вероятность того, что наудачу взятое изделие изготовлено на втором участке, если оно первого сорта. 2.7. Для контроля продукции, состоящей из пяти партий, отобрано наудачу одно изделие. Какова вероятность обнаружить брак, если в одной из партий 2/3 деталей браковано, а в остальных четырех все годные. 2.8. Узел состоит из двух независимо работающих деталей, исправность каждой необходима для работы узла. Первая из деталей за рассматриваемый промежуток времени остается годной с вероятностью 0,8, а вторая – 0,9. Узел вышел из строя. Какова вероятность того, что это произошло из-за неисправности лишь второй детали ? 2.9. Студент сдает зачет, причем получает один вопрос из трех разделов. Первые два раздела одинаковы по объему, а третий в два раза больше первого. Студент знает ответы на 70% вопросов первого раздела, на 50% вопросов второго и на 80% вопросов третьего. Студент зачет сдал. Найти вероятность того, что ему попался вопрос из второго раздела. 2.10. Вероятность того, что деталь изготовленная на первом станке будет первосортной равна 0,7. При изготовлении такой же детали на втором станке эта вероятность равна 0,8. На первом станке изготовлены две детали, а на втором – три. Найти вероятность того, что все детали первосортные.
3. Дискретные случайные величины. Найти неизвестную вероятность Р, математическое ожидание и дисперсию дискретной случайной величины, заданной таблицей распределения вероятностей. Найти функцию распределения. 3.1
3.2
3.3
3.4
3.5
3.6
3.7
3.8
3.9
3.10
4. Нормальный закон распределения. 4.1. Если отклонение размера изделия от номинала менее 0.345, оно относится к высшему сорту. Систематические отклонения исключены, а случайные отклонения подчинены нормальному закону со средним квадратическим отклонением 0.3 мм и математическим ожиданием равным нулю. Какова вероятность того, что два изделия относится к высшему сорту? 4.2. Рост взрослых женщин в одной группе является нормальной случайной величиной с математическим ожиданием 164 см и дисперсией 30,25 см2. Найти вероятность того, что пять случайно выбранных женщин имеют рост не ниже 160 см. 4.3. Если отклонение размера изделия от номинала менее 0.345, оно относится к высшему сорту. Систематические отклонения исключены, а случайные отклонения подчинены нормальному закону со средним квадратическим отклонением 0.3 мм и математическим ожиданием равным нулю. Какова вероятность того, что изделие не относится к высшему сорту? 4.4. Экспериментальное значение предела прочности силикатного кирпича носит случайный характер вследствие имеющихся микротрещин, напряжений и других причин, при этом подчиняется нормальному закону со средним квадратическим отклонением s = 30. Найти вероятность того, что два наудачу взятых кирпича имеют предельную прочность, отличающуюся от теоретического не более чем на 50 . 4.5. Определить среднее квадратическое отклонение случайной ошибки прибора, если ошибка подчиняется нормальному закону распределения с математическим отклонением, равным нулю, и вероятность того, что ошибка лежит в пределах ±20 м равна 0,8. (Указание. 0,8 = 4.6. Средняя прочность основной пряжи а = 60 и с вероятностью 0,9973 прочность лежит в пределах от 48 до 72. Найти вероятность того, что значение прочности находится в пределах от 52 до 68, если прочность распределена нормально. (Указание. При данной вероятности интервал 48 - 72 имеет длину 6σ). 4.7. Номинальные размеры детали 20 х 30 мм. Фактические размеры отклоняются от номинальных, причем отклонения по ширине и длине детали – нормальные независимые случайные величины со средними квадратическими отклонениями 1 мм и 2 мм. Деталь стандартна, если ширина лежит в пределах от 18 до 21 мм, а длина в пределах от 27 до 34 мм. Найти вероятность того, что две случайно взятые детали стандартны. 4.8. Время, необходимое на ремонт прибора, подчиняется нормальному закону распределения с математическим ожиданием 3 ч. и средним квадратическим отклонением 0,5 ч. Какова вероятность того, что на ремонт прибора потребуется не более 4-х ч? 4.9. Прочность пряжи распределена по нормальному закону с математическим ожиданием 60 и средним квадратическим отклонением 5,8 . Пряжа стандартна по прочности, если прочность не меньше 43. Найти вероятность того, что данная партия стандартна. 4.10. Длина заготовки подчинена нормальному закону распределения с математическим ожиданием 10 см и дисперсией 0,25 см2. Из заготовки можно изготовить деталь, если ее длина не меньше 8,5 см. Какова вероятность того, что из заготовки можно изготовить деталь?
5. Построить доверительный интервал для математического ожидания a нормально распределенной генеральной совокупности с известным среднеквадратичным отклонением s с помощью выборки объема n с данным средним выборочным ......................... 6. Исследовать статистически случайную величину X – прочность (разрывная нагрузка), мН, пряжи линейной плотности 18,5 текс. Для этого произведена выборка объема n = 40. Результаты испытаний приведены в таблице. Исследовать статистически случайную величину X – прочность (разрывная нагрузка), мН, пряжи линейной плотности 18,5 текс. Для этого произведена выборка объема n = 40. Результаты испытаний приведены в таблице. 6.1
6.2
6.3
6.4
6.5
6.6
6.7
6.8
6.9
6.10
7. Найти по заданному вариационному ряду выборки выборочное среднее
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

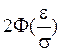 . Зная Ф, по таблице найти ε/σ.)
. Зная Ф, по таблице найти ε/σ.)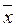 , с заданной надежностью g=0,90
, с заданной надежностью g=0,90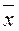 , выборочную дисперсию
, выборочную дисперсию 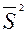 , исправленную выборочную дисперсию
, исправленную выборочную дисперсию 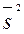 .
.