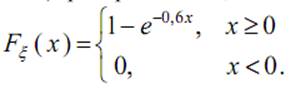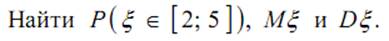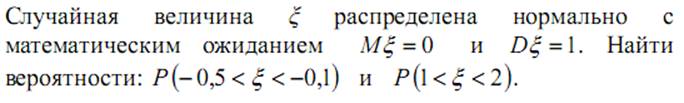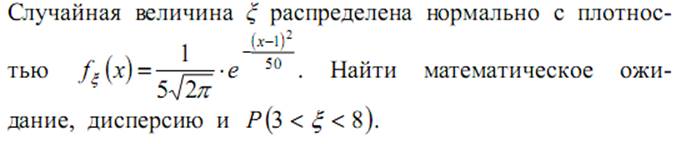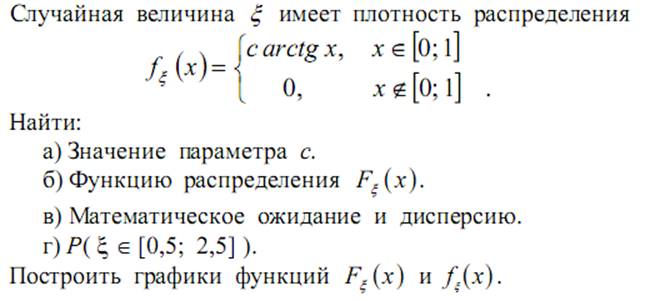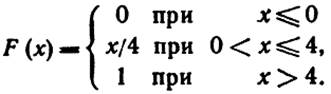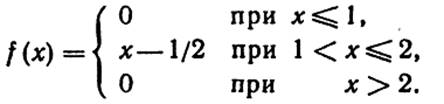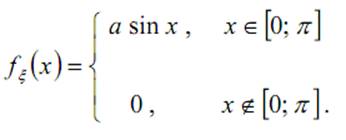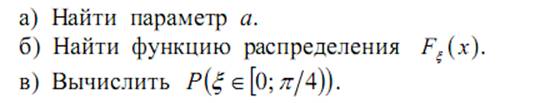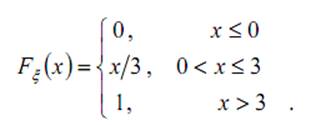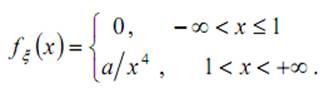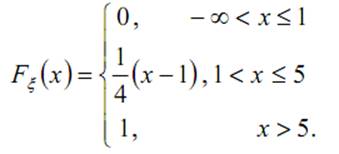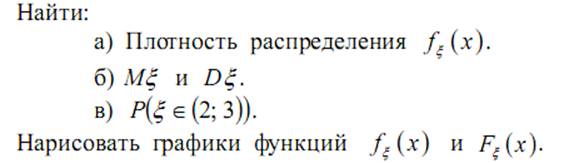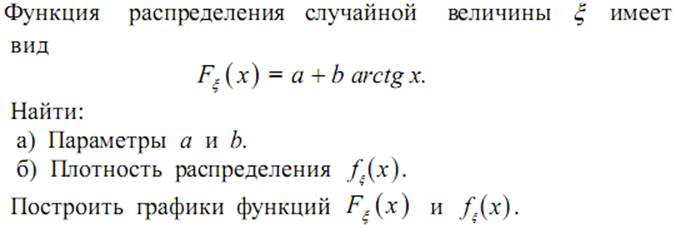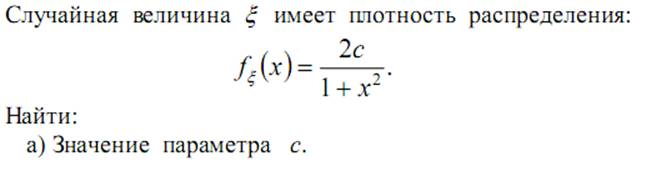Задание на работу

В работе необходимо решить пять задач: пять задач по теории вероятностей. В данных методических указаниях сначала приведены варианты заданий для задач 1-4, а затем – для задачи №5.

ВАРИАНТЫ ЗАДАНИЙ ДЛЯ ЗАДАЧ 1-4

Список задач

1. В коробке шесть одинаковых, занумерованных кубиков. Наудачу по одному извлекают все кубики. Найти вероятность того, что номера извлеченных кубиков появятся в возрастающем порядке.

2. В группе 15 студентов, среди которых 8 отличников. По списку наудачу отобраны 10 студентов. Найти вероятность того, что среди отобранных студентов пять отличников.

3. В коробке пять одинаковых изделий, причем три из них окрашены. Наудачу извлечены два изделия. Найти вероятность того, что среди двух извлеченных изделий окажутся: а) одно окрашенное изделие; б) хотя бы одно окрашенное изделие.

4. Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что наудачу извлеченный кубик имеет окрашенных граней: а) одну; б) две.

5. Задумано двузначное число. Найти вероятность того, что задуманным числом окажется: а) случайно названное двузначное число; б) случайно названное двузначное число, цифры которого различны.

6. В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает три детали. Найти вероятность того, что извлеченные детали окажутся окрашенными.

7. В конверте среди 100 фотокарточек находится одна разыскиваемая. Из конверта наудачу извлечены 10 карточек. Найти вероятность того, что среди них окажется нужная.

8. 14. В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены четыре детали. Найти вероятность того, что среди извлеченных деталей: а) нет бракованных; б) нет годных.

9. Устройство состоит из пяти элементов, из которых два изношены. При включении устройства включаются случайным образом два элемента. Найти вероятность того, что включенными окажутся неизношенные элементы.

10. Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.

11. В цехе работают шесть мужчин и четыре женщины. По табельным номерам наудачу отобраны семь человек. Найти вероятность того, что среди отобранных лиц окажутся три женщины.

11. На складе имеется 15 кинескопов, причем 10 из них изготовлены Львовским заводом. Найти вероятность того, что среди пяти взятых наудачу кинескопов окажутся три кинескопа Львовского завода.

12. В группе 12 студентов, среди которых 5 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов пять отличников.

13. Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что наудачу извлеченный кубик имеет три окрашенные грани.

14. Брошены две игральные кости. Найти вероятности следующих событий: а) сумма выпавших очков равна восьми, если известно, что их разность равна четырем; б) сумма выпавших очков равна пяти, а произведение — четырем.

15. Брошены две игральные кости. Найти вероятности следующих событий: а) сумма выпавших очков равна семи; б) сумма выпавших очков равна восьми, а разность — четырем.

16. Устройство состоит из трех элементов, работающих независимо. Вероятности безотказной работы (за время t) первого, второго и третьего элементов соответственно равны 0,6; 0,7; 0,8. Найти вероятности того, что за время t безотказно будут работать: а) только один элемент; б) только два элемента.

17. Устройство содержит два независимо работающих элемента. Вероятности отказа элементов соответственно равны 0,05 и 0,08. Найти вероятности отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент.

18. Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить четыре бомбы, вероятности попадания которых соответственно равны: 0,3; 0,4; 0,6; 0,7.

19. В ящике 10 деталей, из которых четыре окрашены. Сборщик наудачу взял три детали. Найти вероятность того, что хотя бы одна из взятых деталей окрашена.

20. В пирамиде пять винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки.

21. Два студента условились встретиться в определенном месте между 12 и 13 часами дня. Пришедший первым ждет второго в течение 1/4 часа, после чего уходит. Найти вероятность того, что встреча состоится, если каждый студент наудачу выбирает момент своего прихода (в промежутке от 12 до 13 часов).

22. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором три вопроса.

23. Вероятность попадания в мишень стрелком при одном выстреле равна 0,8. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью, меньшей 0,4, можно было ожидать, что не будет ни одного промаха?

24. Брошены три игральные кости. Найти вероятности следующих событий: а) на двух выпавших гранях появится одно очко, а на третьей грани—другое число очков; в) на всех выпавших гранях появится разное число очков.

25. Брошены три игральные кости. Найти вероятности следующих событий: а) на каждой из выпавших граней появится пять очков; б) на всех выпавших гранях появится одинаковое число очков.

26. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,9. Найти вероятность того, что из двух проверенных изделий только одно стандартное.

27. Наудачу взяты два положительных числа х и у, каждое из которых не превышает единицы. Найти вероятность того, что сумма х+у не превышает единицы, а произведение ху не меньше 0,09.

28. Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,8. Найти вероятность того, что из трех проверенных изделий только два изделия высшего сорта.

29. Наудачу взяты два положительных числа х и у, каждое из которых не превышает двух. Найти вероятность того, что произведение ху будет не больше единицы, а частное у/х не больше двух.

30. Устройство состоит из трех элементов, работающих независимо. Вероятности безотказной работы (за время t) первого, второго и третьего элементов соответственно равны 0,6; 0,7; 0,8. Найти вероятности того, что за время t безотказно будут работать: а) только один элемент; в) все три элемента.

 31. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,05. Составить закон распределения числа отказавших элементов в одном опыте. Найти математическое ожидание числа отказавших элементов в одном опыте. Построить график функции распределения для числа отказавших элементов в одном опыте.

32. В партии 10% нестандартных деталей. Наудачу отобраны четыре детали. Написать биномиальный закон распределения дискретной случайной величины X—числа нестандартных деталей среди четырех отобранных и построить многоугольник полученного распределения. Записать функцию распределения СВ Х.

33. Написать биномиальный закон распределения дискретной случайной величины X—числа появлений «герба» при трех бросаниях монеты и построить многоугольник полученного распределения. Записать функцию распределения СВ Х.

34. Две игральные кости одновременно бросают два раза. Написать биномиальный закон распределения дискретной случайной величины X—числа выпадений четного числа очков на двух игральных костях и построить многоугольник полученного распределения. Записать функцию распределения СВ Х.

35. В партии из шести деталей имеется четыре стандартных. Наудачу отобраны три детали. Составить закон распределения дискретной случайной величины X—числа стандартных деталей среди отобранных и построить многоугольник полученного распределения. Записать функцию распределения СВ Х.

36. Написать биномиальный закон распределения дискретной случайной величины X—числа появлений «герба» при двух бросаниях монеты и построить многоугольник полученного распределения. Записать функцию распределения СВ Х.

37. Дискретная случайная величина X задана законом распределения:

Построить многоугольник распределения СВ Х. Построить график функции распределения СВ Х. Найти математическое ожидание СВ Х и ее дисперсию.

38. Вероятность того, что стрелок попадет в мишень при одном выстреле, равна 0,8. Стрелку выдаются патроны до тех пор, пока он не промахнется. Требуется: а) составить закон распределения дискретной случайной величины X—числа патронов, выданных стрелку; б) найти наивероятнейшее число выданных стрелку патронов.

39. Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0,01. Составить закон распределения дискретной случайной величины X—числа бракованных деталей в партии из 200 деталей. Найти вероятность того, что среди 200 деталей окажется ровно четыре бракованных.

40. Дискретная случайная величина X задана законом распределения:

Построить многоугольник распределения СВ Х. Построить график функции распределения СВ Х. Найти математическое ожидание СВ Х и ее дисперсию.

41. Дискретная случайная величина X задана законом распределения:

Построить многоугольник распределения СВ Х. Построить график функции распределения СВ Х. Найти математическое ожидание СВ Х и ее дисперсию.

42. Устройство состоит из четырех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,2. Составить закон распределения числа отказавших элементов в одном опыте. Найти математическое ожидание числа отказавших элементов в одном опыте. Построить график функции распределения для числа отказавших элементов в одном опыте.

43. В партии 5% нестандартных деталей. Наудачу отобраны пять детали. Написать биномиальный закон распределения дискретной случайной величины X—числа нестандартных деталей среди четырех отобранных и построить многоугольник полученного распределения. Записать функцию распределения СВ Х.

44. В партии из семи деталей имеется четыре стандартных. Наудачу отобраны три детали. Составить закон распределения дискретной случайной величины X—числа стандартных деталей среди отобранных и построить многоугольник полученного распределения. Записать функцию распределения СВ Х.

45. Вероятность того, что стрелок попадет в мишень при одном выстреле, равна 0,9. Стрелку выдаются патроны до тех пор, пока он не промахнется. Требуется: а) составить закон распределения дискретной случайной величины X—числа патронов, выданных стрелку; б) найти наивероятнейшее число выданных стрелку патронов.

46. Испытывают три элемента, которые работают независимо один от другого. Длительность времени безотказной работы элементов распределена по показательному закону: для первого элемента F₁(t) = 1 – e^-0,1t; для второго F₂(t) = 1 – e^-0,2t, для третьего элемента F₃(t) = 1 – e^-0,3t. Найти вероятности того, что в интервале времени (0, 5) ч откажут: а) только один элемент; б) только два элемента.

47. Испытывают три элемента, которые работают независимо один от другого. Длительность времени безотказной работы элементов распределена по показательному закону: для первого элемента F₁(t) = 1 – e^-0,1t; для второго F₂(t) = 1 – e^-0,2t, для третьего элемента F₃(t) = 1 – e^-0,3t. Найти вероятности того, что в интервале времени (0, 7) ч откажут: а) только один элемент; в) все три элемента.

48. Производится испытание трех элементов, работающих независимо один от другого. Длительность времени безотказной работы элементов распределена по показательному закону: для первого элемента f₁(t)=0,1e^-0,1t, для второго f₂(t)=0,2e^-0,2t, для третьего элемента f₃(t)=0,3e^-0,3t. Найти вероятности того, что в интервале времени (0, 10) ч откажут: а) хотя бы один элемент; б) не менее двух элементов.

49. Производится испытание трех элементов, работающих независимо один от другого. Длительность времени безотказной работы элементов распределена по показательному закону: для первого элемента f₁(t)=0,1e^-0,1t, для второго f₂(t)=0,2e^-0,2t, для третьего элемента f₃(t)=0,3e^-0,3t. Найти вероятности того, что в интервале времени (0, 6) ч откажут: а) хотя бы один элемент; б) ровно два элемента.

50. Испытывают три новые микросхемы, которые работают независимо одна от другой. Длительность времени безотказной работы микросхем распределена по показательному закону: для первой схемы F₁(t) = 1 – e^-0,1t; для второй F₂(t) = 1 – e^-0,2t, для третьей схемы F₃(t) = 1 – e^-0,3t. Найти вероятности того, что в интервале времени (0, 8) месяца откажут: а) только две схемы; б) все три микросхемы.

51. Испытывают три новые микросхемы, которые работают независимо одна от другой. Длительность времени безотказной работы микросхем распределена по показательному закону: для первой схемы F₁(t) = 1 – e^-0,1t; для второй F₂(t) = 1 – e^-0,2t, для третьей схемы F₃(t) = 1 – e^-0,3t. Найти вероятности того, что в интервале времени (0, 4) месяцев откажут: а) только одна схема; в) хотя бы одна схема.

52. Производится испытание трех элементов, работающих независимо один от другого. Длительность времени безотказной работы элементов распределена по показательному закону: для первого элемента f₁(t)=0,1e^-0,1t, для второго f₂(t)=0,2e^-0,2t, для третьего элемента f₃(t)=0,3e^-0,3t. Найти вероятности того, что в интервале времени (0, 5) ч откажут: а) ровно один элемент; б) не менее двух элементов.

53. Производится испытание трех элементов, работающих независимо один от другого. Длительность времени безотказной работы элементов распределена по показательному закону: для первого элемента f₁(t)=0,1e^-0,1t, для второго f₂(t)=0,2e^-0,2t, для третьего элемента f₃(t)=0,3e^-0,3t. Найти вероятности того, что в интервале времени (0, 6) ч откажут: а) хотя бы один элемент; б) все три элемента.

54. При работе спецЭВМ в случайные моменты времени возникают неисправности. Время Т работы спецЭВМ от ее включения до возникновения неисправности распределено по показательному закону и в среднем равно 100 дней. Найти вероятность того, что спецЭВМ за 50 дней не откажет.

55. В некоторой организации, работающей круглосуточно, имеется достаточно большое количество вычислительной техники. При  использовании вычислительной техники в среднем каждые 12 минут  возникает неисправность и для ее устранения вызывается техник. Время между вызовами техника распределено по экспоненциальному закону. Требуется определить: 1) среднее число вызовов за год; 2) вероятность того, что на протяжении 24 рабочих часов не возникнет ни одной неисправности.

56. Длительность времени безотказной работы некоторого элемента спецЭВМ имеет показательное распределение и в среднем равно 33,3 дням. Построить математическую модель процесса. Найти вероятность того, что за время длительностью 100 дней: а) элемент откажет; б) элемент не откажет.

57. Испытывают два независимо работающих элемента. Длительности времени безотказной работы обоих элементов имеют показательное распределение. Среднее время безотказной работы первого элемента равно 120 часов, второго элемента – 240 часов. Найти вероятность того, что за время, равное 5 суткам 1) оба элемента не откажут; 2) откажет только один элемент.

58. 54. При работе спецЭВМ в случайные моменты времени возникают неисправности. Время Т работы спецЭВМ от ее включения до возникновения неисправности распределено по показательному закону и в среднем равно 150 дней. Найти вероятность того, что спецЭВМ за 100 дней откажет.

59. В медицинском учреждении, работающем круглосуточно, имеется достаточно большое количество вычислительной техники. При  использовании вычислительной техники в среднем каждые 30 минут  возникает неисправность и для ее устранения вызывается техник. Время между вызовами техника распределено по экспоненциальному закону. Требуется определить: 1) среднее число вызовов за месяц; 2) вероятность того, что на протяжении 8 рабочих часов не возникнет ни одной неисправности.

60. Производится взвешивание некоторого вещества   без систематических  ошибок.  Случайные  ошибки  взвешивания  подчинены  нормальному  закону  со  среднем  квадратичным  отклонением  σ = 20 г.  Найти  вероятность  того,  что  взвешивание   будет   произведено   с   ошибкой,   не   превосходящей  по абсолютной  величины  10 г.

61. Набирая  номер  телефона,  человек  забыл  последние  2  цифры,  помня  при  этом  лишь,  что  они  различные.  Найти  вероятность  того,  что  набран  желаемый  номер.

62. В  круг  радиуса R вписан  правильный   треугольник.   Найти вероятность   того, что точка, брошенная наудачу  в  круг,  попадет в треугольник.

63. Деревянный  куб,  все  грани  которого  окрашены,  распилили на 000  одинаковых кубиков,  которые  положили  в  мешок  и  тщательно  перемешали.   Затем   извлекли   один    кубик. Найти  вероятности  событий:   А –  «кубик  имеет  три  окрашенные  грани»; В – «кубик  не  имеет  ни одной  окрашенной  грани».

64. Деревянный  куб,  все  грани  которого  окрашены,  распилили на 000  одинаковых кубиков,  которые  положили  в  мешок  и  тщательно  перемешали.   Затем   извлекли   один    кубик. Найти  вероятности  событий: А –  «кубик  имеет  две  окрашенные  грани»; В – «кубик  не  имеет  ни одной  окрашенной  грани».

65. Заданы  два  неотрицательных  числа,  которые  не  превосходят  единицу.  Найти  вероятность  того,  что  сумма  этих  чисел  не  превзойдет  единицу,  а  их   произведение будет не больше  2/9.

66. Два   студента   условились   встретиться   в  определенном месте  в  течение  часа.  Первый  пришедший    ждет  второго 15 минут, после  чего уходит.  Найти  вероятность  того,  что  встреча   состоится,   если   каждый  может   прийти   на   нее  случайно  в  любой  момент  указанного  часа.

67. В  урне  находятся  3  белых  и  7  черных  шаров.  Наудачу  извлекли  2  шара.  Найти  вероятность  того,  что  они  будут  белыми.

68. Номер  телефона  состоит  из  6  цифр.  Найти  вероятность  того,   что   у   случайно   набранного   номера   все   цифры  различны.

69. Некто,  набирая  номер  телефона,  забыл  последние  2 цифры,  помня  лишь,  что  они  различны  и  нечетны.  Найти  вероятность  того,  что  будет  набран  нужный  номер.

70. В   урне   находятся  20   белых   и  10   черных   шаров.  Извлекают  наудачу  11   шаров.  Найти   вероятность   того,  что  среди  них окажутся  7  белых.

71. Бросают  5  игральных  костей.  Найти  вероятность  того,  что одно  очко  выпадет,  по  крайней  мере,  на  одной  кости.

72. В  чемпионате  страны  по  футболу  участвуют  16  команд,  которые   разбиты   на  2   одинаковые   подгруппы.   Найти  вероятность  того,  что  2  лучшие  команды  попадут  в  разные  подгруппы.

73.  В  коробке  находятся  75  спичек, среди  которых  5   без   головок.   Берут   наугад  15    спичек.  Найти   вероятность  того,  что  среди  них  будем  иметь  3  спички  без  головок.

74. В   партии   имеется  10   деталей,  7   из   них высшего  качества.  Найти  вероятность  того,  что  из  6  деталей, взятых  наудачу,  4  будут  высшего  качества.

75. На   складе   находятся  100   пар   сапог:  10   пар   имеют  черный  цвет,  остальные –  коричневый.  Наудачу   взяли  8 пар.   Какова   вероятность,   что   все   взятые   пары   будут  коричневыми?

76. В  некоторый  момент  времени  в  лифте  9 – этажного  дома находятся  7  пассажиров.  Найти вероятность   того,  что  2  пассажира  выйдут  на  одном   этаже,   а  остальные  5 – на разных  этажах.

77. Семь   путешественников   случайным   образом   садятся   в  поезд,  имеющий  12  вагонов.  Найти  вероятность  того,  что в   каждый  из   вагонов   сядет  не   более   одного  путешественника.

78. На  спортивной  студенческой    базе  находятся  30  ребят  и  25  девчат.  Для  изучения  мнения  относительно   графика  тренировок   наудачу   отбирают  10   студентов.   Найти вероятность  того,  что  в  эту  группу  попадет  8  ребят  и  2 девчат.

79. В  ящике  находятся  200  яблок,  среди  которых  25  испорчены.  Найти   вероятность   того,   что   среди  10   случайно отобранных   яблок  будут  испорченные.

80. На  книжную  полку  ставят  10  книг.  Найти  вероятность  того,  что  3  определенные  книги  окажутся  рядом.

81. В   группе  25 студентов,  среди  которых  15  юношей.  Было куплено  и  распределено  5  билетов  в  театр.  Найти  вероятность  того,  что  в  театр  пойдут  3  юношей. 

82. Цифры  0;  1;  2;  3;  4;  5;  6;  7;  8;  9   написаны на  карточках,  которые   помещаются   в   урну и тщательно перемешиваются. Из урны наудачу извлекают   две карточки.  Найти   вероятность того, что из них   можно образовать  число,  которое  делится на  18.

83. В коробке шесть одинаковых,   занумерованных кубиков. Наудачу,   по   одному   извлекают все  кубики.   Какова  вероятность  того, что  номера  извлеченных  кубиков  появятся  в  возрастающем  порядке?

84. В ящике находятся 25 деталей первого сорта и  5 деталей второго сорта.  Из   него   наудачу   извлекают  10 деталей.  Найти  вероятность  того, что среди извлеченных деталей  окажутся  две  детали  второго  сорта.

85. В  некотором  цехе  брак  составляет  5%  всех  изделий.  Составить  закон  распределения  ξ  - числа  бракованных  изделий   из  шести   взятых   наудачу.   Найти   математическое  ожидание  и  дисперсию  случайной  величины  ξ. Найти  функцию  распределения СВ  ξ . 

86. Стрелок  производит  шесть  выстрелов  по  мишени.  Вероятность  попадания  при  одном  выстреле  равна  0,2.  Найти  функцию  распределения  ξ   -  числа  попаданий  в  мишень.  С  ее  помощью  найти   P (1≤ ξ ≤ 5).

87. Монету  подбрасывают  6  раз.  Составить  ряд  распределения и построить функцию распределения отношения  числа появления герба к числу появления номинала монеты. Построить многоугольник распределения отношения  числа   появления   герба к числу   появления   номинала монеты.

88. Два  баскетболиста  по  очереди   забрасывают  мяч  в  корзину  с  вероятностью  попадания  при  каждом  броске  для  первого  0,8,   для   второго  -  0,7.  Всего   производится  5  бросков.   Составить   законы   распределения   числа попаданий   для   каждого   игрока,   если   начинает   бросать  первый баскетболист. Найти   математическое  ожидание  и  дисперсию  случайных  величин  (числа попаданий   для   каждого   игрока).

89. Из партии   в  25   деталей,   среди   которых   имеется  6  нестандартных,   выбраны   случайным   образом  3   детали.  Построить   закон   распределения   случайного   числа   ξ   нестандартных  деталей,  содержащихся  в  выборке. Найти   математическое  ожидание  и  дисперсию  случайной  величины  ξ. Найти  функцию  распределения СВ  ξ .

90. В  партии  содержатся  10  деталей,  среди  которых  3  имеют дефект.  Случайно  берут  3  детали.  Найти  закон  распределения,  математическое  ожидание  и  дисперсию  числа  деталей,  оказавшихся  с  дефектом  среди  выбранных. Найти  функцию  распределения СВ  ξ .

91. Из  партии  деталей  берется   последовательно  для  контроля  по одной  детали.  Если  взятая  деталь  имеет  дефект,  то  контроль  на  этом  завершается.  Исходя  из  этих  условий,  были  проверены  не  более  5  деталей.  Вероятность  того,  что   деталь   имеет   дефект, равна  0,1.   Найти   закон  распределения,   математическое   ожидание   и   дисперсию  числа  проверенных  деталей.

92. Из  урны,  содержащей  5  белых  и  3  черных  шара,  извлекают   последовательно   по   одному  шару   до   появления белого.  Найти   закон   распределения,   математическое  ожидание   и   дисперсию   числа   вынутых   черных  шаров,  если  вынутый  шар  обратно  в  урну  не  возвращается.

93. Делаются  попытки  открыть  замок,  имея  в  распоряжение  8  ключей,  которые  берутся  наудачу.  Найти  закон  распределения,   математическое   ожидание   и   дисперсию   числа попыток  в  случае,  когда ключ,  которым  сделана  неудачная  попытка,  исключается  из  дальнейшего  выбора.

94. Делаются  попытки  открыть  замок,  имея  в  распоряжение  8  ключей,  которые  берутся  наудачу.  Найти  закон  распределения,   математическое   ожидание   и   дисперсию   числа попыток  в  случае,  когда ключ,   которым   сделана неудачная попытка, не исключается  из  дальнейшего  выбора.

95. Бросаются  2  игральные  кости.  Пусть   ξ –     произведение  числа   выпавших   очков   на   обеих   костях.  Найти   закон  распределения,   математическое   ожидание,   дисперсию   и  среднее  квадратное  отклонение  случайной  величины  ξ.

96. Проверяется  функционирование  некоторого  устройства.  Вероятность   того,   что   оно   не   функционирует,   равна  0,2.  Найти  закон  распределения  числа  испорченных  устройств,  если   проверяется  10    устройств.   Найти   математическое  ожидание,  дисперсию  и  среднее  квадратичное  отклонение этого  числа.

97. Длительность времени безотказной работы некоторого элемента спецЭВМ имеет показательное распределение и в среднем равно 50 дням. Построить математическую модель процесса. Найти вероятность того, что за время длительностью 100 дней: а) элемент откажет; б) элемент не откажет.

98. Результаты  измерения  расстояния между  двумя  населенными  пунктами  подчинены  нормальному  закону  распределения  с  параметрами  а = 16 км,  σ  = 100 м.  Найти  вероятности  того,  что   расстояние  между  этими  пунктами: а)  не  менее  15,8 км; б)  не  более  16,25 км;

99. Рост   взрослого  мужчины   является   случайной   величиной распределенной  нормально.  Пусть  cм 170 = ξ M ,  = ξ D 36 см.  Вычислить  вероятность  того,  что  хотя  бы  один  из  наудачу  выбранных  четырех  мужчин  будет   иметь   рост   от  168 см   до  172 см.

100. Непрерывная  случайная  величина  ξ   имеет  показательное  (экспоненциальное)  распределение,  а

101.

102. Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка: а) меньшая 0,04; б) большая 0,05.

103. Автомат штампует детали. Контролируется длина детали X, которая распределена нормально с математическим ожиданием (проектная длина), равным 50 мм. Фактически длина изготовленных деталей не менее 32 и не более 68 мм. Найти вероятность того, что длина наудачу взятой детали: а) больше 55 мм; б) меньше 40 мм.

104. Производится измерение диаметра вала без систематических (одного знака) ошибок. Случайные ошибки измерения X подчинены нормальному закону со средним квадратическим отклонением 10 мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 15 мм.

105. Производится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону со средним квадратическим отклонением 20 г. Найти вероятность того, что взвешивание будет произведено с ошибкой, не превосходящей по абсолютной величине 10 г.

106. Случайная величина X распределена нормально с математическим ожиданием 10. Вероятность попадания X в интервал (10, 20) равна 0,3. Чему равна вероятность попадания X в интервал (0, 10)?

107.

108. Рост   взрослого   человека   является   случайной   величиной,  имеющей  нормальное  распределение.  Пусть  средний  рост  равен  175  см,  а  среднее  квадратичное  отклонение – 6  см.   Найти   вероятность   того,   что   хотя   бы   один   из   пяти  человек,  взятых  наудачу,  будет  иметь  рост  между  170 см  и  180 см.

ЗАДАЧА №5

1.

2.

3.

Случайная величина X задана плотностью распределения f(x) = c(x²+2x) в интервале (0; 1); вне этого интервала f(x) = 0. Найти

а) параметр с;

б) математическое ожидание СВ X;

в) функцию распределения F(x).

4.

5.

6.

7.

8.

9.

Случайная величина X задана плотностью распределения f(x) = (1/2)x в интервале (0; 2); вне этого интервала f(x) = 0. Найти

а) математическое ожидание СВ X;

б) функцию распределения F(x);

в) нарисовать графики функций f(x) и F(x).

10.

11.

12.

13.

Случайная величина X задана плотностью распределения f(x) = 2x в интервале (0; 1); вне этого интервала f(x) = 0. Найти

а) математическое ожидание СВ X;

б) функцию распределения F(x);

в) нарисовать графики функций f(x) и F(x).

14.

Случайная величина X задана функцией распределения

Найти:

а) математическое ожидание СВ X;

б) функцию плотности f(x);

в) нарисовать графики функций f(x) и F(x).

15.

16.

Случайная величина X задана плотностью распределения

Найти:

а) математическое ожидание СВ X;

б) функцию распределения F(x);

в) нарисовать графики функций f(x) и F(x).

17.

18.

Случайная  величина  ξ  имеет  плотность  распределения

19.

Задана  функция  распределения  случайной  величины  ξ:

20.

Случайная  величина  ξ  имеет  плотность  распределения

21.

Случайная   величина   ξ  имеет  функцию   распределения

22.

23.

24.

25.

26.

27.