Помимо метода наименьших квадратов, с помощью которого в большинстве случаев определяются неизвестные параметры модели регрессии, в случае линейной модели парной регрессии осуществим иной подход к решению данной проблемы.

Линейная модель парной регрессии может быть записана в виде:

где у – значения зависимой переменной;

х – значения независимой переменной;

– среднее значение зависимой переменной, которое определяется на основании выборочных данных вычисленное по формуле средней арифметической:

уi– значения зависимой переменной,

n – объём выборки;

– среднее значение независимой переменной, которое определяется на основании выборочных данных вычисленное по формуле средней арифметической: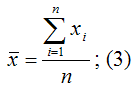

Параметр βyx называется выборочным коэффициентом регрессии переменной у по переменной х. Данный параметр показывает, на сколько в среднем изменится зависимая переменная у при изменении независимой переменной х на единицу своего измерения.

Выборочный коэффициент регрессии переменной у по переменной х рассчитывается по формуле: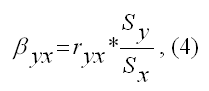

где ryx – это выборочный парный коэффициент корреляции между переменными у и х, который рассчитывается по формуле:

– среднее арифметическое значение произведения зависимой и независимой переменных:

Sy – показатель выборочного среднеквадратического отклонения зависимой переменной у. Этот показатель характеризует, на сколько единиц в среднем отклоняются значения зависимой переменной у от её среднего значения. Он рассчитывается по формуле:

– среднее значение из квадратов значений зависимой переменной у:

– квадрат средних значений зависимой переменной у:

Sx – показатель выборочного среднеквадратического отклонения независимой переменной х. Этот показатель характеризует, на сколько единиц в среднем отклоняются значения независимой переменной х от её среднего значения. Они рассчитывается по формуле: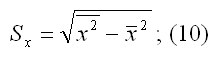

– среднее значение из квадратов значений независимой переменной х: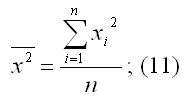

– квадрат средних значений независимой переменной х:

При использовании рассмотренного подхода оценивания неизвестных параметров линейной модели парной регрессии, следует учитывать что ryx=rxy, однако βyx≠βxy.