| Главная » Учебно-методические материалы » СТАТИСТИКА » Курс социально-экономической статистики. Под ред. Назарова М.Г. |
| 23.01.2012, 00:01 | |
53.1. Корреляционный анализКорреляционный анализ является одним из методов статистического анализа взаимозависимости нескольких признаков. Основная задача корреляционного анализа состоит в оценке корреляционной матрицы генеральной совокупности по выборке и определении на основе этой матрицы частных и множественных коэффициентов корреляции и детерминации. Парный и частный коэффициенты корреляции характеризуют тесноту линейной зависимости между двумя переменными соответственно на фоне действия и при исключении влияния всех остальных показателей, входящих в модель. Они изменяются в пределах от -1 до +1, причем чем ближе коэффициент корреляции к 1, тем сильнее зависимость между переменными. Если коэффициент корреляции больше нуля, то связь положительная, а если меньше нуля — отрицательная. Множественный коэффициент корреляции характеризует тесноту, линейной связи между одной переменной (результативной) и остальными, входящими в модель; он изменяется в пределах от 0 до 1. Квадрат множественного коэффициента корреляции называется множественным коэффициентом детерминации. Он характеризует долю дисперсии одной переменной (результативной), обусловленной влиянием всех остальных переменных (аргументов), входящих в модель. Исходной для анализа является матрица
размерности п х k, i-я строка которой характеризует i-е наблюдение (объект) по всем k показателям (j = 1, 2, ..., k). В корреляционном анализе матрицу Х рассматривают как выборку объема п из k-мерной генеральной совокупности, подчиняющейся k-мерному нормальному закону распределения. По выборке определяют оценки параметров генеральной совокупности, а именно: вектор средних
где
xij — значение i-го наблюдения j-го фактора, ril — выборочный парный коэффициент корреляции, характеризующий тесноту линейной связи между показателями xj и xl. При этом rjl является оценкой генерального парного коэффициента корреляции. Матрица R является симметричной (rjl = rlj) и положительно определенной. Кроме того, находятся точечные оценки частных и множественных коэффициентов корреляции любого порядка. Например, частный коэффициент корреляции (k - 2)-го порядка между переменными х1 и х2 равен
где Rjl — алгебраическое дополнение элемента rjl корреляционной матрицы R. При этом Rjl = (-l)j+l Mjl, где Mjl — минор, т.е. определитель матрицы, получаемой из матрицы R путем вычерчивания j-й строки и l-го столбца. Множественный коэффициент корреляции (k - 1)-го порядка результативного признака x1 определяется по формуле
где | R | — определитель матрицы R. Значимость частных и парных коэффициентов корреляции, т.е. гипотеза H0: ρ = 0, проверяется по t-критерию Стьюдента. Наблюдаемое значение критерия находится по формуле
где r — соответственно оценка частного или парного коэффициента корреляции ρ; l — порядок частного коэффициента корреляции, т.е. число фиксируемых факторов (для парного коэффициента корреляции l=0). Напомним, что проверяемый коэффициент корреляции считается значимым, т.е. гипотеза H0: ρ = 0 отвергается с вероятностью ошибки α, если tнабл по модулю будет больше, чем значение tкр, определяемое по таблицам t-распределения для заданного α и υ = n – l - 2. Значимость коэффициентов корреляции можно также проверить с помощью таблиц Фишера — Иейтса. При определении с надежностью у доверительного интервала для значимого парного или частного коэффициента корреляции р используют Z-преобразование Фишера и предварительно устанавливают интервальную оценку для Z:
где tγ вычисляют по таблице значений интегральной функции Лапласа из условия
значение Z' определяют по таблице Z-преобразования по найденному значению r. Функция Z' — нечетная, т.е.
Обратный переход от Z к ρ осуществляют также по таблице Z-преобразования, после использования которой получают интервальную оценку для ρ с надежностью γ:
Таким образом, с вероятностью γ гарантируется, что генеральный коэффициент корреляции ρ будет находиться в интервале (rmin, rmax). Значимость множественного коэффициента корреляции (или его квадрата — коэффициента детерминации) проверяется по F-критерию. Например, для множественного коэффициента корреляции проверка значимости сводится к проверке гипотезы, что генеральный множественный коэффициент корреляции равен нулю, т.е. H0 : ρ1/2,…,k = 0, а наблюдаемое значение статистики находится по формуле
Множественный коэффициент корреляции считается значимым, т.е. имеет место линейная статистическая зависимость между х1 и остальными факторами х2, ..., хk, если Fнабл > Fкр, где Fкр определяется по таблице F-распределения для заданных α, υ1 = k - 1, υ2 = n - k. 53.2. Регрессионный анализРегрессионный анализ — это статистический метод исследования зависимости случайной величины у от переменных (аргументов) хj (j = 1, 2,..., k), рассматриваемых в регрессионном анализе как неслучайные величины независимо от истинного закона распределения xj. Обычно предполагается, что случайная величина у имеет нормальный закон распределения с условным математическим ожиданием Для проведения регрессионного анализа из (k + 1)-мерной генеральной совокупности (у, x1, х2, ..., хj, ..., хk) берется выборка объемом n, и каждое i-е наблюдение (объект) характеризуется значениями переменных (уi, xi1, хi2, ..., хij, ..., xik), где хij — значение j-й переменной для i-го наблюдения (i = 1, 2,..., n), уi — значение результативного признака для i-го наблюдения. Наиболее часто используемая множественная линейная модель регрессионного анализа имеет вид
где βj — параметры регрессионной модели; εj — случайные ошибки наблюдения, не зависимые друг от друга, имеют нулевую среднюю и дисперсию σ2. Отметим, что модель (53.8) справедлива для всех i = 1,2, ..., n, линейна относительно неизвестных параметров β0, β1,…, βj, …, βk и аргументов. Как следует из (53.8), коэффициент регрессии Bj показывает, на какую величину в среднем изменится результативный признак у, если переменную хj увеличить на единицу измерения, т.е. является нормативным коэффициентом. В матричной форме регрессионная модель имеет вид
где Y — случайный вектор-столбец размерности п х 1 наблюдаемых значений результативного признака (у1, у2,.... уn); Х— матрица размерности п х (k + 1) наблюдаемых значений аргументов, элемент матрицы х,, рассматривается как неслучайная величина (i = 1, 2, ..., n; j=0,1, ..., k; x0i, = 1); β — вектор-столбец размерности (k + 1) х 1 неизвестных, подлежащих оценке параметров модели (коэффициентов регрессии); ε — случайный вектор-столбец размерности п х 1 ошибок наблюдений (остатков). Компоненты вектора εi не зависимы друг от друга, имеют нормальный закон распределения с нулевым математическим ожиданием (Mεi = 0) и неизвестной постоянной σ2 (Dεi = σ2). На практике рекомендуется, чтобы значение п превышало k не менее чем в три раза. В модели (53.9)
В первом столбце матрицы Х указываются единицы при наличии свободного члена в модели (53.8). Здесь предполагается, что существует переменная x0, которая во всех наблюдениях принимает значения, равные единице. Основная задача регрессионного анализа заключается в нахождении по выборке объемом п оценки неизвестных коэффициентов регрессии β0, β1, …, βk модели (53.8) или вектора β в (53.9). Так как в регрессионном анализе хj рассматриваются как неслучайные величины, a Mεi = 0, то согласно (53.8) уравнение регрессии имеет вид
для всех i = 1, 2, ..., п, или в матричной форме:
где Для оценки вектора-столбца β наиболее часто используют метод наименьших квадратов, согласно которому в качестве оценки принимают вектор-столбец b, который минимизирует сумму квадратов отклонений наблюдаемых значений уi от модельных значений
где символом «Т» обозначена транспонированная матрица. Наблюдаемые и модельные значения результативного признака у показаны на рис. 53.1.
Рис. 53.1. Наблюдаемые и модельные значения результативного признака у Дифференцируя, с учетом (53.11) и (53.10), квадратичную форму Q по β0, β1, …, βk и приравнивая частные производные к нулю, получим систему нормальных уравнений
решая которую получим вектор-столбец оценок b, где b = (b0, b1, ..., bk)T. Согласно методу наименьших квадратов, вектор-столбец оценок коэффициентов регрессии получается по формуле
ХT — транспонированная матрица X; (ХTХ)-1 — матрица, обратная матрице ХTХ. Зная вектор-столбец b оценок коэффициентов регрессии, найдем оценку
или в матричном виде:
Оценка ковариационной матрицы вектора коэффициентов регрессии b определяется выражением
где
Учитывая, что на главной диагонали ковариационной матрицы находятся дисперсии коэффициентов регрессии, имеем
Значимость уравнения регрессии, т.е. гипотеза Н0: β = 0 (β0,= β1 = βk = 0), проверяется по F-критерию, наблюдаемое значение которого определяется по формуле
По таблице F-распределения для заданных α, v 1 = k + l,v2 = n – k - l находят Fкр. Гипотеза H0 отклоняется с вероятностью α, если Fнабл > Fкр. Из этого следует, что уравнение является значимым, т.е. хотя бы один из коэффициентов регрессии отличен от нуля. Для проверки значимости отдельных коэффициентов регрессии, т.е. гипотезы Н0: βj = 0, где j = 1, 2, ..., k, используют t-критерий и вычисляют tнабл(bj) = bj / Гипотеза H0 отвергается с вероятностью α, если tнабл > tкр. Из этого следует, что соответствующий коэффициент регрессии βj значим, т.е. βj ≠ 0. В противном случае коэффициент регрессии незначим и соответствующая переменная в модель не включается. Тогда реализуется алгоритм пошагового регрессионного анализа, состоящий в том, что исключается одна из незначительных переменных, которой соответствует минимальное по абсолютной величине значение tнабл. После этого вновь проводят регрессионный анализ с числом факторов, уменьшенным на единицу. Алгоритм заканчивается получением уравнения регрессии со значимыми коэффициентами. Существуют и другие алгоритмы пошагового регрессионного анализа, например с последовательным включением факторов. Наряду с точечными оценками bj генеральных коэффициентов регрессии βj регрессионный анализ позволяет получать и интервальные оценки последних с доверительной вероятностью γ. Интервальная оценка с доверительной вероятностью γ для параметра βj имеет вид
где tα находят по таблице t-распределения при вероятности α = 1 - γ и числе степеней свободы v = п - k - 1. Интервальная оценка для уравнения регрессии
Интервал предсказания
где tα определяется по таблице t-распределения при α = 1 - γ и числе степеней свободы v = п - k - 1. По мере удаления вектора начальных условий х0 от вектора средних
Рис. 53.2. Точечная Мультиколлинеарность Одним из основных препятствий эффективного применения множественного регрессионного анализа является мультиколлинеарность. Она связана с линейной зависимостью между аргументами х1, х2, ..., хk. В результате мультиколлинеарности матрица парных коэффициентов корреляции и матрица (XTX) становятся слабообусловленными, т.е. их определители близки к нулю. Это приводит к неустойчивости оценок коэффициентов регрессии (53.12), завышению дисперсии s На практике о наличии мультиколлинеарности обычно судят по матрице парных коэффициентов корреляции. Если один из элементов матрицы R больше 0,8, т.е. | rjl | > 0,8, то считают, что имеет место мультиколлинеарность, и в уравнение регрессии следует включать один из показателей — хj или xl. Чтобы избавиться от этого негативного явления, обычно используют алгоритм пошагового регрессионного анализа или строят уравнение регрессии на главных компонентах. Пример. Построение регрессионного уравнения Согласно данным двадцати (п = 20) сельскохозяйственных районов, требуется построить регрессионную модель урожайности на основе следующих показателей: у — урожайность зерновых культур (ц/га); x1 — число колесных тракторов (приведенной мощности) на 100 га; х2 — число зерноуборочных комбайнов на 100 га; х3 — число орудий поверхностной обработки почвы на 100 га; x4 — количество удобрений, расходуемых на гектар; х5 — количество химических средств оздоровления растений, расходуемых на гектар. Исходные данные для анализа приведены в табл. 53.1. Таблица 53.1 Исходные данные для анализа
Решение. С целью предварительного анализа взаимосвязи показателей построена матрица R — таблица парных коэффициентов корреляции.
Анализ матрицы парных коэффициентов корреляции показывает, что результативный признак наиболее тесно связан с показателем х4 — количеством удобрений, расходуемых на гектар (ryx4 = 0,58). В то же время связь между аргументами достаточно тесная. Так, существует практически функциональная связь между числом колесных тракторов (x1) и числом орудий поверхностной обработки почвы x3(rx1x3) = 0,98. О наличии мультиколлинеарности свидетельствуют также коэффициенты корреляции rx1x2 = 0,85 и rx3x2 = 0,88. Чтобы продемонстрировать отрицательное влияние мультиколлинеарности, рассмотрим рассчитанное на ЭВМ регрессионное уравнение урожайности, включив в него все исходные показатели:
(-0,01) (0,72) (0,13) (2,90) (-0,95) В скобках указаны tнабл (βj) = tj — расчетные значения t-критерия для проверки гипотезы о значимости коэффициента регрессии Н0: βj = 0, j = 1, 2, 3, 4, 5. Критическое значение tкр = 1,76 найдено по таблице t-распределения при уровне значимости α = 0,1 и числе степеней свободы v = 14. Из уравнения следует, что статистически значимым является коэффициент регрессии только при х4, так как |t4| = 2,90 > tкр = 1,76. Не поддаются экономической интерпретации отрицательные значения коэффициентов регрессии при х1 и x5, из чего следует, что повышение насыщенности сельского хозяйства колесными тракторами (х1) и средствами оздоровления растений (x5) отрицательно сказывается на урожайности. Таким образом, полученное уравнение регрессии неприемлемо. После реализации алгоритма пошагового регрессионного анализа с исключением переменных и учетом того, что в уравнение должна войти только одна из трех тесно связанных переменных (x1, х2 или x3), получаем окончательное уравнение регрессии
(11,12) (2,09) (3,02) Уравнение значимо при α = 0,05, так как Fнабл = 266 > Fкр = 3,20, найденного по таблице F-распределения при α = 0,05, v1 = 3 и v2 = 17. Значимы и коэффициенты регрессии β1 и β4, так как |tj| > tкр = 2,11 (при α = 0,05, v = 17). Коэффициент регрессии β1 следует признать значимым (β1 ≠ 0) из экономических соображений; при этом t1 = 2,09 лишь незначительно меньше tкр = 2,11. В случае если α = 0,1, tкр = 1,74 и коэффициент регрессии β1 статистически значим. Из уравнения регрессии следует, что увеличение на единицу числа тракторов на 100 га пашни приводит к росту урожайности зерновых в среднем на 0,345 ц/га (b1 = 0,345). Коэффициенты эластичности Э1 = 0,068 и Э4 = 0,161 (Эj = Множественный коэффициент детерминации r 53.3. Компонентный анализКомпонентный анализ предназначен для преобразования системы k исходных признаков в систему k новых показателей (главных компонент). Главные компоненты не коррелированы между собой и упорядочены по величине их дисперсий, причем первая главная компонента имеет наибольшую дисперсию, а последняя, k-я — наименьшую. При этом выявляются неявные, непосредственно не измеряемые, но объективно существующие закономерности, обусловленные действием как внутренних, так и внешних причин. Компонентный анализ является одним из основных методов факторного анализа. В задачах снижения размерности и классификации обычно используются т первых компонент (т << k). При наличии результативного признака у может быть построено уравнение регрессии на главных компонентах. На основании матрицы исходных данных
размерности п х k, где хij.— значение j-го показателя у i-го наблюдения (i = 1, 2, ..., n; j = 1, 2, .... k), вычисляют средние значения показателей
с элементами
Рассчитывается матрица парных коэффициентов корреляции:
с элементами
где j, l= 1, 2, .... k. На главной диагонали матрицы R, т.е. при j = l, расположены элементы
Модель компонентного анализа имеет вид
где aiv — «вес», т.е. факторная нагрузка v-й главной компоненты на j-ю переменную; fiv — значение v-й главной компоненты для i-го наблюдения (объекта), где v = 1, 2, ...,k. В матричной форме модель (53.26) имеет вид
fiv — значение v-й главной компоненты для i-го наблюдения (объекта); aiv — значение факторной нагрузки v-й главной компоненты на j-ю переменную. Матрица F описывает п наблюдений в пространстве k главных компонент. При этом элементы матрицы F нормированы, т.е. fv =
Выражение (53.28) может быть представлено в виде
С целью интерпретации элементов матрицы А рассмотрим выражение для парного коэффициента корреляции между переменной zj и, например, f1-й главной компонентой. Так как zо и f1 нормированы, будем иметь с учетом (53.26):
Принимая во внимание (53.29), окончательно получим
Рассуждая аналогично, можно записать в общем виде
для всех j = 1, 2, .,., k и v = 1, 2, .... k. Таким образом, элемент ajv матрицы факторных нагрузок А характеризует тесноту линейной связи между исходной переменной zj и главной компонентой fv, т.е. –1 ≤ ajv ≤ +1. Рассмотрим теперь выражение для дисперсии нормированной переменной zj. С учетом (53.26) будем иметь
где v, v'= 1, 2, ..., k. Учитывая (53.29), окончательно получим
По условию, переменные zj нормированы и s Полный вклад v-й главной компоненты в дисперсию всех k исходных признаков вычисляется по формуле
Одно из основополагающих условий метода главных компонент связано с представлением корреляционной матрицы R через матрицу факторных нагрузок А. Подставив для этого (53.27) в (53.24), будем иметь
Учитывая (53.28), окончательно получим
Перейдем теперь непосредственно к отысканию собственных значений и собственных векторов корреляционной матрицы R. Из линейной алгебры известно, что для любой симметричной матрицы R всегда существует такая ортогональная матрица U, что выполняется условие
Так как матрица R положительно определена, т.е. ее главные миноры положительны, то все собственные значения λv > 0 для любых v =1, 2, ..., k. В компонентном анализе элементы матрицы Λ ранжированы: λ1 ≥ λ2 ≥ ... ≥ λv ... ≥ λk ≥ 0. Как будет показано ниже, собственное значение λv характеризует вклад v-й главной компоненты в суммарную дисперсию исходного признакового пространства. Таким образом, первая главная компонента вносит наибольший вклад в суммарную дисперсию, а последняя, k-я, — наименьший. В ортогональной матрице U собственных векторов v-й столбец является собственным вектором, соответствующим λv -му значению. Собственные значения λ1 ≥ ... ≥ λv.... ≥ λk находятся как корни характеристического уравнения
Собственный вектор Vv, соответствующий собственному значению λv корреляционной матрицы R, определяется как отличное от нуля решение уравнения, которое следует из (53.34):
Нормированный собственный вектор Uv равен
Из условия ортогональности матрицы U следует, что U-1 = UT, но тогда, по определению, матрицы R и Λ подобны, так как они, согласно (53.34), удовлетворяют условию
Так как у подобных матриц суммы диагональных элементов равны, то
Учитывая, что сумма диагональных элементов матрицы R равна k, будем иметь
Таким образом,
Представим матрицу факторных нагрузок А в виде
а v-й столбец матрицы А — как
где Uv — собственный вектор матрицы R, соответствующий собственному значению λv. Найдем норму вектора Аv:
Здесь учитывалось, что вектор Uv — нормированный и U
Сравнив полученный результат с (53.32), можно сделать вывод, что собственное значение λv характеризует вклад v-й главной компоненты в суммарную дисперсию всех исходных признаков. Из (53.38) следует, что
Согласно (53.37), общий вклад всех главных компонент в суммарную дисперсию равен k. Тогда удельный вклад v-й главной компоненты определяется по формуле Суммарный вклад т первых главных компонент определяется из выражения Обычно для анализа используют т первых главных компонент, вклад которых в суммарную дисперсию превышает 60—70%. Матрица факторных нагрузок А используется для экономической интерпретации главных компонент, которые представляют собой линейные функции исходных признаков. Для экономической интерпретации fv используются лишь те хj, для которых |ajv| > 0,5. Значения главных компонент для каждого i-го объекта (i = 1, 2, .... n) задаются матрицей F. Матрицу значений главных компонент можно получить из формулы
откуда
Уравнение регрессии на главных компонентах строится по алгоритму пошагового регрессионного анализа, где в качестве аргументов используются главные компоненты, а не исходные показатели. К достоинству последней модели следует отнести тот факт, что главные компоненты не коррелированы. При построении уравнений регрессии следует учитывать все главные компоненты. Пример. Построение регрессионного уравнения По данным примера из § 53.2 провести компонентный анализ и построить уравнение регрессии урожайности Y на главных компонентах. Решение. В примере из § 53.2 пошаговая процедура регрессионного анализа позволила исключить отрицательное значение мультиколлинеарности на качество регрессионной модели за счет значительной потери информации. Из пяти исходных показателей в окончательную модель вошли только два (x1 и x4). Более рациональным в условиях мультиколлинеарности можно считать построение уравнения регрессии на главных компонентах, которые являются линейными функциями всех исходных показателей и не коррелированы между собой. Воспользовавшись методом главных компонент, найдем собственные значения и на их основе — вклад главных компонент в суммарную дисперсию исходных показателей x1, х2, х3, х4, х5 (табл. 53.2). Таблица 53.2 Собственные значения главных компонент
Ограничимся экономической интерпретацией двух первых главных компонент, общий вклад которых в суммарную дисперсию составляет 89,0%. В матрице факторных нагрузок
звездочкой указаны элементы аjv = rxjfv, учитывающиеся при интерпретации главных компонент fv, где j, v = 1, 2, ..., 5. Из матрицы факторных нагрузок А следует, что первая главная компонента наиболее тесно связана со следующими показателями: x1 — число колесных тракторов на 100 га (a11 = rx1f1 = 0,95); х2 — число зерноуборочных комбайнов на 100 га (rx2f1 = 0,97); х3 — число орудий поверхностной обработки почвы на 100 га (rx3f1 = 0,94). В этой связи первая главная компонента — f1 — интерпретирована как уровень механизации работ. Вторая главная компонента — f2 — тесно связана с количеством удобрений (х4) и химических средств оздоровления растений (x5), расходуемых на гектар, и интерпретирована как уровень химизации растениеводства. Уравнение регрессии на главных компонентах строится по данным вектора значений результативного признака Y и матрицы F значений главных компонент. Некоррелированность главных компонент между собой и тесноту их связи с результативным признаком у показывает матрица парных коэффициентов корреляции (табл. 53.3). Анализ матрицы парных коэффициентов корреляции свидетельствует о том, что результативный признак у наиболее тесно связан с первой (ryf1 = 0,48), третьей (ryf3 = 0,37) и. второй (ryf2 = 0,34) главными компонентами. Можно предположить, что только эти главные компоненты войдут в регрессионную модель у. Таблица 53.3 Матрица парных коэффициентов корреляции
Первоначально в модель у включают все главные компоненты (в скобках указаны расчетные значения t-критерия):
Качество модели характеризуют: множественный коэффициент детерминации r Если значимость уравнения регрессии (гипотеза Н0: β1 = β2 = β3 = β4 = 0 проверялась при α = 0,05, то значимость коэффициентов регрессии, т.е. гипотезы H0: βj = 0 (j = 1, 2, 3, 4), следует проверять при уровне значимости, большем, чем 0,05, например при α = 0,1. Тогда при α = 0,1, v = 14 величина tкр = 1,76, и значимыми, как следует из уравнения (53.41), являются коэффициенты регрессии β1, β2, β3. Учитывая, что главные компоненты не коррелированы между собой, можно сразу исключить из уравнения все незначимые коэффициенты, и уравнение примет вид
Сравнив уравнения (53.41) и (53.42), видим, что исключение незначимых главных компонент f4 и f5, не отразилось на значениях коэффициентов уравнения b0 = 9,52, b1 = 0,93, b2 = 0,66 и соответствующих tj (j = 0, 1, 2, 3). Это обусловлено некоррелированностью главных компонент. Здесь интересна параллель уравнений регрессии по исходным показателям (53.22), (53.23) и главным компонентам (53.41), (53.42). Уравнение (53.42) значимо, поскольку Fнабл = 194 > Fкр = 3,01, найденного при α = 0,05, v1 = 4, v2 = 16. Значимы и коэффициенты уравнения, так как tj > tкр. = 1,746, соответствующего α = 0,01, v = 16 для j = 0, 1, 2, 3. Коэффициент детерминации r Уравнение (53.42) характеризуется средней относительной ошибкой аппроксимации Уравнение регрессии на главных компонентах (53.42) обладает несколько лучшими аппроксимирующими свойствами по сравнению с регрессионной моделью (53.23) по исходным показателям: r | |


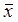 , вектор средних квадратических отклонений s и корреляционную матрицу R порядка k:
, вектор средних квадратических отклонений s и корреляционную матрицу R порядка k:
 (53.1)
(53.1) (53.2)
(53.2) (53.3)
(53.3) (53.4)
(53.4) (53.5)
(53.5)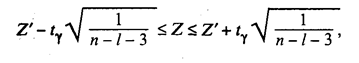 (53.6)
(53.6)


 (53.7)
(53.7) (53.8)
(53.8) (53.9)
(53.9)
 (53.10)
(53.10) (53.11)
(53.11) — вектор-столбец с элементами
— вектор-столбец с элементами  1...,
1..., 


 (53.12)
(53.12)
 уравнения регрессии
уравнения регрессии (53.13)
(53.13)

 (53.14)
(53.14) (53.15)
(53.15) (53.16)
(53.16) (53.17)
(53.17)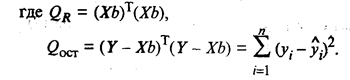
 bj. По таблице t-распределения для заданного α и v = п - k - 1 находят tкр.
bj. По таблице t-распределения для заданного α и v = п - k - 1 находят tкр. (53.19)
(53.19) , x
, x ,,..., x
,,..., x )T записывается в виде
)T записывается в виде (53.20)
(53.20) (53.21)
(53.21) ширина доверительного интервала при заданном значении γ будет увеличиваться (рис. 53.2), где
ширина доверительного интервала при заданном значении γ будет увеличиваться (рис. 53.2), где  ).
).
 и интервальная
и интервальная  оценки уравнения регрессии
оценки уравнения регрессии  .
. , оценок этих коэффициентов (53.14), так как в их выражения входит обратная матрица (XTX)-1, получение которой связано с делением на определитель матрицы (ХTХ). Отсюда следуют заниженные значения t(bj). Кроме того, мультиколлинеарность приводит к завышению значения множественного коэффициента корреляции.
, оценок этих коэффициентов (53.14), так как в их выражения входит обратная матрица (XTX)-1, получение которой связано с делением на определитель матрицы (ХTХ). Отсюда следуют заниженные значения t(bj). Кроме того, мультиколлинеарность приводит к завышению значения множественного коэффициента корреляции.

 ) показывают, что при увеличении показателей x1 и х4 на 1% урожайность зерновых повышается соответственно на 0,068% и 0,161%.
) показывают, что при увеличении показателей x1 и х4 на 1% урожайность зерновых повышается соответственно на 0,068% и 0,161%.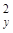 = 0,469 свидетельствует о том, что только 46,9% вариации урожайности объясняется вошедними в модель показателями (x1 и x4), т.е. насыщенностью растениеводства тракторами и удобрениями. Остальная часть вариации обусловлена действием неучтенных факторов (х2, x3, х5, погодными условиями и др.). Средняя относительная ошибка аппроксимации
= 0,469 свидетельствует о том, что только 46,9% вариации урожайности объясняется вошедними в модель показателями (x1 и x4), т.е. насыщенностью растениеводства тракторами и удобрениями. Остальная часть вариации обусловлена действием неучтенных факторов (х2, x3, х5, погодными условиями и др.). Средняя относительная ошибка аппроксимации 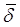 = 10,5% свидетельствует об адекватности модели, так же как и величина остаточной дисперсии s2 = 1,97.
= 10,5% свидетельствует об адекватности модели, так же как и величина остаточной дисперсии s2 = 1,97.
 а также s1, ..., sk и матрицу нормированных значений
а также s1, ..., sk и матрицу нормированных значений

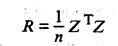 (53.24)
(53.24) (53.25)
(53.25)
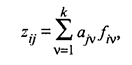 (53.26)
(53.26) (53.27)
(53.27)
 , a главные компоненты не коррелированы между собой. Из этого следует, что
, a главные компоненты не коррелированы между собой. Из этого следует, что  (53.28)
(53.28)
 (53.29)
(53.29)

 (53.30)
(53.30)
 (53.31)
(53.31) = 1. Таким образом, дисперсия переменной zj, согласно (53.31), представлена своими составляющими, определяющими долю вклада в нее всех k главных компонент.
= 1. Таким образом, дисперсия переменной zj, согласно (53.31), представлена своими составляющими, определяющими долю вклада в нее всех k главных компонент.  (53.32)
(53.32)
 (53.33)
(53.33)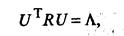 (53.34)
(53.34)
 (53.35)
(53.35) (53.36)
(53.36)



 (53.37)
(53.37)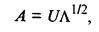 (53.38)
(53.38)
 (53.39)
(53.39) Uv = 1. Таким образом,
Uv = 1. Таким образом, 
 (53.40)
(53.40) .
. .
.




 (53.41)
(53.41) (53.42)
(53.42)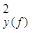 = 0,486 > r
= 0,486 > r = 0,469;
= 0,469;  = 9,99% <
= 9,99% < 