| Главная » Учебно-методические материалы » СТАТИСТИКА » Общая теория статистики: учебник. Под ред. Елисеевой И.И. |
| 23.01.2012, 19:59 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
11.6. Показатели концентрации, специализации, монополизации. Многомерная структураМетоды и показатели анализа структуры используются при изучении таких важных экономических процессов, как концентрация производства, специализация предприятий или отраслей, диверсификация капитала, степень монополизации рынка и др. В гл. 5 рассмотрены показатели специализации предприятий региона, зоны, основанные на измерении вариации объемов производства или долей предприятий, а также отношения фактических мер вариации к предельно возможным при данной численности совокупности. В предыдущем параграфе данной главы рассмотрены показатели концентрации объема признака, основанные на неравномерности его распределения между единицами совокупности. Но эти характеристики не исчерпывают проблемы. Даже равномерное распределение производства, скажем, автомобилей в стране, где всего три предприятия, производящих по 33,3% всего выпуска автомашин, говорит о высокой степени концентрации в данной отрасли, и вероятности его монополизации, для устранения конкуренции и получения монопольной прибыли. Следовательно, показатель концентрации должен учитывать две величины: численность совокупности и степень неравномерности распределения признака между ее единицами. Рассмотрим методику конструирования показателя по заданным его свойствам. Проще построить показатель, учитывающий численность совокупности и быстро убывающий, как убывает степень концентрации и вероятность монополизации, с ростом числа производителей п. Можно эту составляющую желаемого показателя представить например, как величину, обратную числу единиц совокупности, т. е. 1 : п. При одном предприятии имеем абсолютный максимум, равный единице; при п = 2, п = 3, п = 4 доля все еще довольно значительна, но при большом п (большом числе производителей товара или услуг) эта составляющая уже становится несущественно малой и главное значение приобретает вторая составляющая - степень неравномерности распределения объема признака между единицами совокупности. Чтобы построить показатель, рассмотрим, как зависит от степени неравномерности распределения признака сумма накопленных долей объема признака При этом условии минимальная сумма накопленных долей будет в том случае, когда доли всех единиц совокупности кроме последней, равны нулю, а доля последней («монополиста») равна единице. Сумма накопленных долей тоже равна единице. Итак, Найдем теперь выражение для максимума этой суммы, которая, согласно условию ранжирования, образуется при строгом равенстве всех долей, каждая из которых будет равна 1 : п. Нарастающие доли будут 1 : п, 2: п, 3 : п, и т. д. до п : п, а их сумма, как сумма членов арифметической прогрессии, выражается как: (1 : п) (1 + 2 + ... + п) = (1 : п)(п2 + п) : 2 = (п + 1) : 2. Чем дальше отстоит фактическая сумма накопленных долей от максимальной величины, тем сильнее неравномерность распределения. Следовательно, в числителе должны стоять величины: [(п + 1) : 2] - 1 = (n + 1 - 2): 2 = (п - 1) : 2. Итак, показатель степени концентрации за счет неравномерности распределения имеет форму: Теперь, объединяем обе составляющие и получаем окончательный показатель степени концентрации объема признака в совокупности, состоящей из п единиц, проранжированных в порядке возрастания объема признака или доли его у данной единицы в общем объеме признака в совокупности. Обозначим его К: Можно произвести преобразование этой формулы, но по нашему мнению, лучше сохранить выражения обеих составляющих частей, чтобы их разная природа оставалась явной для пользователя. Остается выяснить свойства предлагаемого показателя концентрации и меры возможности монополизации рынка. При единственном монополисте: п = 1, первое слагаемое будет равно единице, второе -нулю. В итоге весь коэффициент равен единице. При п = 2 и равномерном распределении объема признака При сосредоточении всего объема признака у второго предприятия Эта величина показателя К максимальная из возможных. При росте п первое слагаемое уменьшается и при п ® ¥ стремится к нулю. Второе слагаемое при концентрации всего производства у одного предприятия всегда остается равной единице, значит, при абсолютной концентрации К ® 1 при п®¥. При полной равномерности, когда второе слагаемое равно нулю, имеем: К ® 0 при n ® ¥, как и должно быть логически., При реальных значениях распределений объема признака между единицами совокупности получаем промежуточные значения между [(1 : п) + 1] и 1 : п. Рассмотрим, например, распределение производителей грузовых автомашин в России в 1994 г. (табл. 11.7). Таблица 11.7 Концентрация производства грузовых автомашин, в РФ 1994 г.*
Показатель степени концентрации производства грузовых автомобилей в РФ в 1994 г. составил: Величина показателя указывает на значительную, хотя,и не очень высокую, степень концентрации, большая часть которой следует из неравномерности распределения производства между фирмами. Опасность монополизации невелика. По-существу, она еще меньше, ибо грузовые автомашины разных фирм не вполне однородны, и нельзя рассматривать, как взаимозаменяющие товары. Из последнего замечания следует, что при экономической оценке величины концентрации и возможностей монополизации нельзя принимать в расчет только величину какого-то показателя, но надо проверить, насколько однородным является сам объемный признак, распределение которого изучается. Даже хлеб, мясо и другие подобные товары на самом деле неоднородны по сортам, видам и т. п. Чем разнообразнее ассортимент товара, тем меньше, при прочих равных условиях, возможность монополизации производства. Качественная вариация, как и количественная вариация долей, облегчает конкуренцию. Рассмотрим, измерение степени специализации привлекая методику многомерной характеристики структуры. Как известно, основным показателем специализации экономики считаются доли разных товаров, или их групп, или отраслей в общем объеме реализации продукции и услуг. Однако, нельзя игнорировать также структуру затрат труда, материалов, а в сельском хозяйстве - структуру использованных земельных ресурсов и т. д. Поэтому, более обоснованное суждение о специализации предприятия или региона можно получить с помощью многомерных показателей структуры, полученных тем или иным способом. В качестве примера рассмотрим показатели специализации в растениеводстве АПК Вологодской области (табл. 11.8). Как видим, в стоимости продукции лен занимает первое место. При одномерной характеристике специализации только на основе стоимости продукции надо было бы считать область льноводческой и кормодобывающей. Но нельзя игнорировать, что зерновые занимают более 50% в материальных затратах и первое место (почти половину) в затратах труда, а также и то, что лен занимает лишь 1,5% площади посева. Построим многомерные показатели структуры, тремя способами. Первый - с помощью простой арифметической средней величины долей. Очевидно, при этом полагаем все четыре признака структуры равноправными, что, конечно, является упрощением реальности. Второй способ состоит в вычислении взвешенных средних долей. При этом весами служат экспертные оценки сравнительной важности признаков специализации. Предположим, что наименее ценному признаку - доле в площади, присвоен балл 1, в затратах труда - балл 2, в материальных затратах - балл 3, наиболее ценному признаку - стоимости продукции - балл 5. Тогда можно рассчитать взвешенные по баллам средние доли. Они приведены в предпоследней графе табл. 11.8. Теперь, растениеводство надо признать специализированным на кормодобывании и зерновом производстве, но существенную роль играет и льноводство. Таблица 11.8 Показатели специализации растениеводства (АПК Вологодской обл., 1995 г.)*
Третий способ построения многомерных средних долей не требует привлечения каких-либо субъективных экспертных оценок -используется только информация, содержащаяся в исходных долях. Более информативным, а следовательно, весомым признается тот признак, который имеет более высокий коэффициент детерминации долей со всеми остающимися Признаками. Вычислив попарные и средние коэффициенты детерминации, примем меньший из них за единицу (один балл) и получим баллы для других признаков, как отношения их средних коэффициентов детерминации к меньшему (см. табл. 11.9). Таблица 11.9 Матрица коэффициентов детерминации долей
Как видим, полученные баллы сильно расходятся с принятыми экспертными оценками по второму способу. Расходятся и многомерные доли, взвешенные по новым, информационным баллам, (на основе коэффициентов детерминации) приведенные в последней графе табл. 11.8. Резко снизился удельный вес льноводства, а на первое место вышло производство зерна. 11.7. Абсолютные и относительные показатели изменения структурыОб особенностях измерения динамики относительных величин, в том числе и долей было сказано в п. 9.3. Здесь излагаются показатели, характеризующие не изменение отдельной доли, а изменение структуры в целом, т. е.«структурный сдвиг». Нередко под этим понятием Понимают хорошо и давно известные индексы влияния изменения структуры на среднюю Величину относительного показателя, например, показателей эффективности: производительности труда, себестоимости продукции, урожайности, рентабельности и т. п. Эти индексы измеряют не величину самого изменения структуры, а его влияние (они рассмотрены в гл. 10). Обратимся к примеру (табл. 11.10). Таблица 11.10 Изменение структуры ВВП России*
Эти данные свидетельствуют о существенном изменении долей ВВП, использованных на разные цели. Обобщающим абсолютным показателем изменения структуры может служить сумма модулей абсолютных изменений долей, выраженная в процентных пунктах:
В 1995 г. по сравнению с 1992 г. это абсолютное изменение, обозначенное Ad, составило 31,8 процентных пункта. Расчет среднего абсолютного изменения, приходящегося на одну долю (группу, единицу совокупности) не дает никакой добавочной информации, ибо отношение среднего изменения к величине средней доли тождественно суммарному изменению в отношении к сумме долей, равной единице. Зато очень важно определить, насколько сильно произошедшее изменение структуры в сравнении с предельно возможной величиной суммы модулей. Логически ясно, что максимальная сумма модулей изменения долей равна 2. Например, была одна доля в пределе равная 0, другая равная 1, а в следующем периоде наоборот. Сумма модулей разности долей равна 2. Теперь можно построить показатель степени интенсивности абсолютного структурного сдвига KAd:
По данным табл. 11.10. Изменение структуры использования ВВП страны на 16% всего за 3 года следует признать весьма быстрым. Чтобы избежать взаимопогашения разных по знаку изменений долей, вместо модулей можно применить квадраты и получить квадратическую меру абсолютного структурного сдвига, в форме среднего квадратического изменения долей: По данным табл. 11.10.
В данном случае, все доли изменились почти на одинаковое число пунктов, поэтому средняя квадратическая величина почта, равна арифметической средней: 31,8 : 4 = 7,95. При резко различных изменениях долей квадратическое изменение ближе к наибольшему из изменений, чем арифметическая средняя. Предельная величина суммы квадратов изменения долей также равна 2, как и сумма модулей изменений долей, так как 12 = 1 (-1)2 = 1. Для четырех долей максимальное значение sd = Ö2̅ ̅: ̅4̅ =0,71. Фактическое значение составило 0,0798 : 0,71 =0,112 или 11,2% максимального. Абсолютные показатели изменения долей не учитывают величины долей базисного периода, т. е. считается, что изменение доли на 10 процентных пунктов равнозначно, была ли доля до этого равна 2% или 50%. Такой подход недостаточен. Ведь первая из долей при увеличении на 10 процентных пунктов возросла в 6 раз, а вторая только на одну пятую часть. Очевидно, изменение структуры следует охарактеризовать и относительным показателем, измеряющим среднее относительное изменение долей. Рассмотрим построение этого показателя. Средний темп изменения долей, взвешенный по величине базисных долей, тождественно равен 1: Невзвешенный средний темп изменения при разных долях не обязательно равен 1, но из-за взаимопогашения темпов, больших 1 и темпов, меньших 1, близок к 1 и ничего не говорит о мере изменения структуры. Наиболее информативным оказывается среднее относительное линейное изменение (темп прироста) по модулю: По данным табл. 11.10 эта величина составляет: .
Этот показатель означает, что при изменении структуры использования ВВП России произошел в среднем 38-й процентный сдвиг - изменение роли статей в итоге. Величина Id предела не имеет, так как малая доля может возрасти в бесконечно большое число раз. Использовать необходимо лишь простую среднюю из относительных .изменений долей, так как средняя величина, взвешенная по базисным долям, как легко можно убедиться, всегда равна ранее рассмотренному абсолютному изменению Аd. К. Гатевым, С. В. Курышевой, Т. Н. Агаповой предложен еще ряд показателей относительного изменения структуры, о которых желающие расширить свои знания могут прочитать в указанной в конце главы литературе. 11.8. Ранговые и инновационнце показатели изменения структурыИзменения структуры не сводятся к возрастанию и уменьшению долей элементов этой структуры. В ряде Практических задач особую роль играют ранги долей. Представим себе, что в каком-то комитете, на конференции, в Государственной Думе РФ, и т. Д. обсуждался законопроект, и, по мере внесения в него поправок, проводилось три голосования, результаты которых представлены в табл. 11.11. Таблица 11.11 Результаты голосования по законопроекту
При втором голосовании в сравнении с первым произошло существенное изменение структуры вотумов: абсолютное изменение (по модулю) A^2/i =17+3+14= 34 процентных пункта, среднее изменение по 11,33 пункта на элемент. Абсолютный сдвиг при третьем голосовании в сравнении со вторым намного скромнее: Аd2/1 = 6+5+1=12 или по 4 пункта на элемент структуры. Однако, качественное различие структур второго и третьего голосований принципиально, а различие второго и первого голосований не принципиально. И в первом и во втором голосовании законопроект не принят, а в третьем он одобрен. Это качественное различие проявилось в изменении рангов вотумов. Аналогичную ситуацию имеем в ряде других явлений. Так в результате экзаменационной сессии ранг («место», занятое группой) может быть гораздо важнее (скажем - группа, занявшая I и II места, награждаются путевкой, ценным призом) чем величина различия в долях отличников, «хорошистов», троечников и двоечников. Изменение рангов статей платежного баланса страны, рангов статей в структуре ВПП может иметь гораздо большее экономическое значение, чем даже значительный абсолютный структурный сдвиг без изменения рангов. На основе изменения рангов долей можно построить два показателя: 1. Линейный коэффициент изменения рангов долей. Обозначим его KR. Он представляет собой отношение фактической суммы модулей изменения рангов к предельно возможной сумме модулей при п элементах структуры, равной (п2 : 2) для четного и (п2 - 1) : 2 для нечетного п:
По данным табл. 11.11 этот коэффициент составил
Изменение рангов на 50% максимального, конечно, является существенным преобразованием структуры. Если подсчитать по ней ранги долей по данным табл. 11.10 получим: 2.1 Квадратический коэффициент изменения рангов долей KRK. Для его построения используем известный коэффициент корреляции оангов Спирмена (см. гл. 8). При полном совпадении рангов долей в базисном и текущем периодах коэффициент Спирмена равен +1. При максимальном изменении рангов (первый становится последним, порядок рангов «переворачивается») коэффициент Спирмена составит -1, следовательно максимальное значение изменения коэффициента Спирмена равно 2. Чтобы построить показатель степени интенсивности изменения рангов элементов структуры, следует отклонение фактического коэффициента Спирмена от единицы разделить на 2. Получим формулу KRK:
где R1i и R0i - ранги долей элементов структуры в базисном и отчетном периодах. Измерим с помощью этого показателя структурный сдвиг в распределении банков Санкт-Петербурга по сумме активов, рассматривая только банки, действовавшие и в 1994, и в 1995 гг. (табл. 11.12). Что касается измерения сдвига с обновлением состава элементов структуры, эта проблема рассмотрена ниже.
Рассмотрим, в заключение инновационные показатели изменения структуры, т. е. характеристики степени обновления ее качественного состава и элементов. Воспользуемся в качестве примера таблицей из уже упоминавшейся монографии Т. Н. Агаповой (табл. 11.13). Линейный коэффициент интенсивности абсолютного структурного сдвига Таблица 11.12 Изменение рангов банков Санкт-Петербурга по сумме активов
Таблица 11.13 Изменение и обновление структуры посевной площади сельскохозяйственного предприятия
Для построения рангового коэффициента логично будет условиться приписать нулевым значениям элементов последние по порядку ранги, если таких элементов несколько - в порядке их рангов в другом периоде. Тогда получим:
Квадратический коэффициент интенсивности изменения рангов: Все три показателя указывают на сильный количественный сдвиг в структуре. Но в отличие от ранее рассмотренных примеров, в данном примере нельзя этим ограничиться. Произошло качественное обновление структуры, состава сельскохозяйственных культур, и это качественное изменение отразится следующими показателями: 1. Показатель обновления по числу элементов структуры - отношение числа выбывших и числа новых элементов структуры к общему числу имевшихся разных элементов за оба периода, его можно назвать «коэффициентом обновления состава»: где ЧВ, ЧН - число выбывших и число новых элементов: П0 и П1 - число элементов базисной и текущей структуры.
2. Принимая во внимание не только число обновившихся элементов структуры, но и их доли, т. е. значение в системе, получим отношение суммы обновившихся долей к максимальной сумме, как уже известно, равной двум целым. Этот показатель назовем «коэффициентом обновления долей» где dВ, dН - выбывшие и новые доли; к1 и к2 - их число. В данном примере имеем: КОД (0,14 + 0,20 +0,30) : 2 = 0,32 или 32% максимального показателя. При полном обновлении всех элементов структуры оба коэффициента обновления равны единице или 100%, так как числа выбывших и новых элементов равны в сумме числам прежних и новых элементов, а суммы выбывших долей и новых долей дают в числителе показателя КОД 2, и 2 в знаменателе. При отсутствии качественного обновления элементов структуры оба коэффициента, естественно, равны нулю, хотя количественный сдвиг может быть очень велик. Например, если при 20 элементах структуры 10 элементов имели по 0,01 и 10 элементов по 0,09, а в следующем периоде размеры их полностью поменяются, то абсолютный показатель интенсивности структурного сдвига достигнет (10∙0,08 + 10∙0,08) : 2 = 0,8 или 80% максимального. Напротив, при сильном качественном обновлении, например, 18 элементов структуры из 20, если сумма долей этих обновившихся элементов составляет всего 0,18, а 2 доли, составляющие в сумме 0,82, остались неизменными, то количественные меры структурного сдвига окажутся низкими, хотя коэффициент обновления достигает по числу элементов: КОС = 18 : 20 = 0,9 или 90% максимального. Приведенные примеры показывают, что при анализе изменения структуры следует применить не какой-то один показатель, а всю их систему, так как каждый показатель отражает, измеряет особый аспект структурного сдвига. Разные показатели изменения структуры связаны между собой не жесткой связью, а связью статистической, в среднем - прямой зависимостью, но в конкретных процессах изменения структуры разные показатели могут сильно расходиться и даже изменяться в разных направлениях. Изменение структуры сложных систем включает не только изменение состава и долей материальных элементов структуры, но также изменение структуры связей между этими элементами. Об изучении структуры связей, в частности, коэффициента детерминации при многофакторной регрессии см. гл. 8. Рекомендуемая литература к главе 11 1. Агапова Т. Н. Методы статистического изучения структуры сложных систем и ее изменения. - М.: Финансы и статистика, 1996. 2. Казинец Л. С. Измерение структурных сдвигов в экономике. - М.: Экономика, 1969. 3. Казинец Л. С. Темпы роста и структурные сдвиги в экономике. - М.: Экономика, 1981. 4. Гатев К. Статистическая оценка различий между структурами / Теоретические и методологические проблемы статистики / М., Статистика, 1979. 5. Елисеева И. И., Рукавишников В. Н. Группировка, корреляция, распознавание образов. - М.: Статистика, 1977. 6. Миркин Б. Г. Анализ качественных признаков и структур. - М.: Статистика, 1980. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

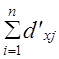 при условии, что изучаемая совокупность проранжирована в порядке нарастания долей объема признака.
при условии, что изучаемая совокупность проранжирована в порядке нарастания долей объема признака.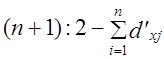 . Чтобы измерить степень отклонения от равномерности распределения, нужно сравнить меру фактической неравномерности с максимально возможной, равной разности между максимально возможной суммой накопленных долей и минимальной их суммой, равной единице. Следовательно, знаменатель должен иметь вид:
. Чтобы измерить степень отклонения от равномерности распределения, нужно сравнить меру фактической неравномерности с максимально возможной, равной разности между максимально возможной суммой накопленных долей и минимальной их суммой, равной единице. Следовательно, знаменатель должен иметь вид: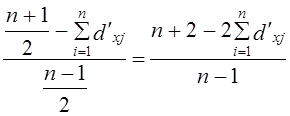 (11.4)
(11.4)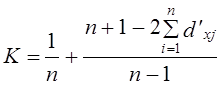 (11.5)
(11.5)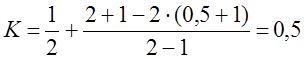
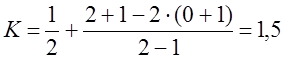
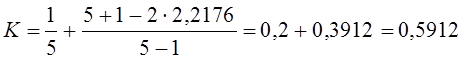
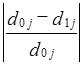

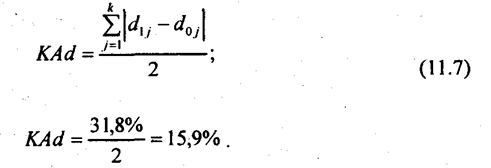
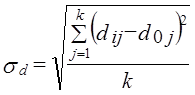 (11.8)
(11.8)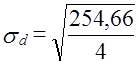 = 7,98 процентных пункта.
= 7,98 процентных пункта.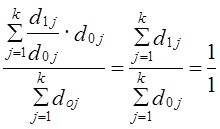 .
.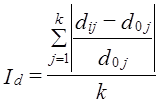 . (11.9)
. (11.9)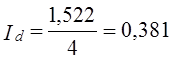 или 38,1 % (а не пункта).
или 38,1 % (а не пункта).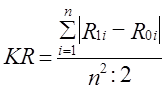 или
или 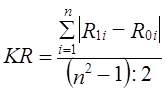 . (11.10)
. (11.10)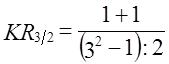 = 0,5 или 50%.
= 0,5 или 50%.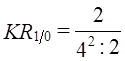 = 0,25 , или 25% максимального, что также следует признать значительным изменением. О социально-экономическом значении этого изменения («хорошо» или «плохо») можно спорить, ибо сокращение доли накопления, да еще приабсолютном снижении всего объема ВВП, подрывает перспективы роста экономики в будущие годы.
= 0,25 , или 25% максимального, что также следует признать значительным изменением. О социально-экономическом значении этого изменения («хорошо» или «плохо») можно спорить, ибо сокращение доли накопления, да еще приабсолютном снижении всего объема ВВП, подрывает перспективы роста экономики в будущие годы.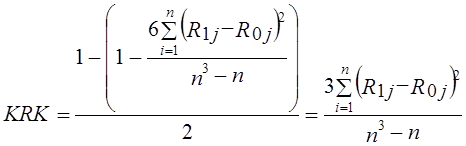 , (11.11)
, (11.11)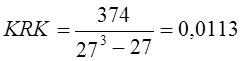 или 1,13%, что говорит об устойчивости иерархии петербургских банков, изменение их рангов за год было несущественным.
или 1,13%, что говорит об устойчивости иерархии петербургских банков, изменение их рангов за год было несущественным.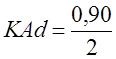 = 0,45 или 45% максимального.
= 0,45 или 45% максимального.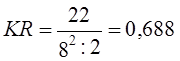 или 68,8% максимального.
или 68,8% максимального.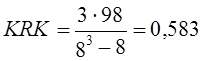 или 58,3% максимального значения.
или 58,3% максимального значения.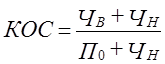 или
или 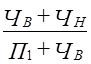 , (11.12)
, (11.12)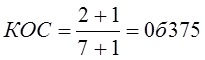 или 37,5% предельной величины.
или 37,5% предельной величины.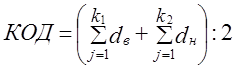 ,
,