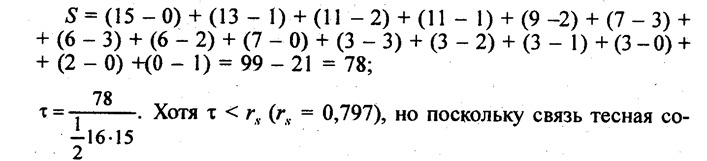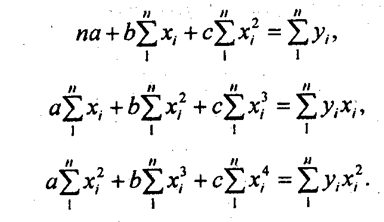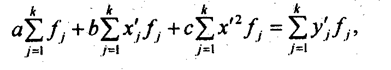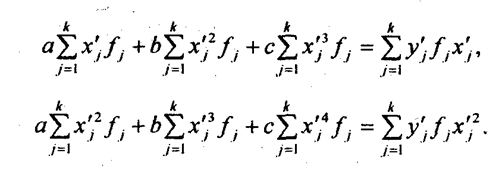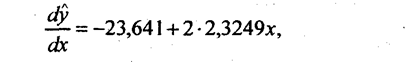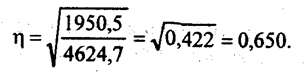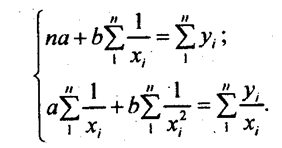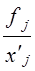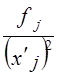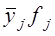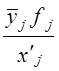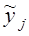| Главная » Учебно-методические материалы » СТАТИСТИКА » Общая теория статистики: учебник. Под ред. Елисеевой И.И. |
| 23.01.2012, 16:53 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
8.6. Применение парного линейного уравнения регрессииПрежде чем обсуждать вопросы использования уравнений парной регрессии, напомним, что парный корреляционный анализ не дает чистых мер влияния только одного изучаемого фактора. Если факторы взаимосвязаны, то парная связь измеряет влияние данного фактора и часть влияния прочих факторов, связанных с ним. И все же при тесной связи уравнение регрессии может стать полезным орудием анализа экономических, технологических, социальных или природных процессов. Сравнивая фактические уровни надоя в табл. 8.1 с расчетными, т. е. такими, которые были бы получены при фактических затратах средств на корову и средней по совокупности эффективности, измеряемой коэффициентом регрессии, можно найти отклонения уi –˜уi. Они показывают, насколько хозяйство получило от коров больше или меньше молока в условиях фактической эффективности использования средств, чем при средней по совокупности эффективности использования средств. Так, в хозяйстве № 6 получено от коровы в среднем 31,8 ц молока, хотя при низком уровне затрат 1355 руб. на корову и средней эффективности затрат было бы получено только по 26,5 ц молока. Фактически надой составил 120% к расчетному. Наоборот, хозяйство № 9 получило по 26,7 ц вместо расчетных 35,6 ц. Следовательно, эффективность использования средств на производство молока в этом хозяйстве (1616 руб. на корову) составила только 26,7 : 35,7 = 75% средней по совокупности. Оценка хозяйственной деятельности по отклонениям от расчетных значений показателей на основе уравнений регрессии (тем более на основе многофакторных регрессионных моделей) гораздо более оправдана и содержательна, чем оценка результатов производства по отклонениям от среднего значения результативного признака в совокупности без учета факторов - характеристик возможностей и природных условий предприятия. Уравнения регрессии применимо и для прогнозирования возможных ожидаемых значений результативного признака. При этом следует учесть, что перенос закономерности связи, измеренной в варьирующей совокупности, в статике на динамику не является, строго говоря, корректным и требует проверки условий допустимости такого переноса (экстраполяции), что выходит за рамки статистики и может быть сделано только специалистом, хорошо знающим объект (систему) и возможности его развития в будущем. Ограничением прогнозирования на основании регрессионного уравнения, тем более парного, служит условие стабильности или по крайней мере малой изменчивости других факторов и условий изучаемого процесса, не связанных с ними. Если резко изменится "внешняя среда" протекающего процесса, прежнее уравнение регрессии результативного признака на факторный потеряет свое значение. В сильно засушливый год доза удобрений может не оказать влияния на урожайность сельскохозяйственной культуры, так как последнюю лимитирует недостаточная влагообеспеченность. Прогнозируемое значение результативного показателя получается при подстановке в уравнение регрессии ожидаемой величины факторного признака. Так, если подставить в уравнение (8.14) расход средств на корову, равный 2200 руб., то получим ожидаемый надой молока от коровы, равный 55,85 ц. При таком прогнозировании следует соблюдать еще одно ограничение: нельзя подставлять значения факторного признака, значительно отличающиеся от входящих в базисную информацию, по которой вычислено уравнение регрессии. При качественно иных уровнях фактора, если они даже возможны в принципе, были бы другими параметры уравнения. Можно рекомендовать при определении значений факторов не выходить за пределы трети размаха вариации как за минимальное, так и за максимальное значение признака-фактора, имевшееся в исходной информации. Прогноз, полученный подстановкой в уравнение регрессии ожидаемого значения фактора, называют точечным прогнозом. Вероятность точной реализации такого прогноза крайне мала. Необходимо сопроводить его значением средней ошибки прогноза или доверительным интервалам прогноза с достаточно большой вероятностью. Средняя ошибка положения линии регрессии в генеральной совокупности при значении факторного признака, равном хk, вычисляется для линии регрессии по формуле (8.20) где тỹk - средняя ошибка положения линии регрессии в генеральной совокупности при х = хk, п - объем выборки; хk - ожидаемое значение фактора; syост - оценка среднего квадратического отклонения результативного признака от линии регрессии в генеральной совокупности с учетом степеней свободы вариации. По данным табл. 8.1 находим syост . При хл = 2200 руб. на 1 голову имеем: Для вычисления доверительных границ прогноза линии регрессии нужно умножить ее среднюю ошибку на t-критерий Стьюдента. При 14 степенях свободы и доверительной вероятности 0,95 (a = 0,05) значение t-критерия равно 2,14. Получаем доверительные границы: 55,85 ± 2,629·2,14, или от 50,22 до 61,48 ц от 1 коровы. Интервал довольно широкий. Значительная неопределенность прогноза линии регрессии связана с малым объемом выборки. При объеме совокупности, равном 400, и той же вариации надоев ошибка прогноза была бы в 5 раз меньше и доверительный интервал был бы уже. Средняя ошибка прогноза для индивидуального значения по правилу о дисперсии суммы независимых переменных образуется из ошибки прогноза положения линии регрессии и среднего квадратического отклонения индивидуальных значений от линии регрессии (остаточной вариации), т. е. В нашем примере имеем: Доверительные границы прогноза индивидуальных значений надоя молока на корову при расходе 2200 руб. на 1 голову составляют с вероятностью нахождения внутри границ, равной 0,95: 55,85 ± 4,568·2,14, или от 46,07 до 65,63 ц. Главным источником ошибки неопределенности прогноза индивидуальных значений служит не столько неопределенность прогноза линии регрессии, сколько значительная вариация надоев за счет других факторов, кроме входящих в уравнение регрессии. 8.7. Вычисление параметров парной линейной корреляции на основе аналитической группировкиВ главе 6 рассмотрен метод аналитической группировки, позволяющий установить наличие, вид и форму связи признаков. Но группировка не дает меры тесноты связи и уравнения регрессии. Теперь, пользуясь методикой корреляционно-регрессионного анализа, можно дополнить аналитическую группировку вычислением этих мер связи. Возьмем в качестве примера приведенную в главе 6 группировку и рассчитаем необходимые показатели (см. табл. 8.2). Таблица 8.2 Расчет корреляции по аналитической группировке
Коэффициент линейной регрессии свободный член уравнения регрессии а = у̅ - bх̅ = 11,77 - (-0,18·63) = 23,15. Итак, имеем уравнение связи: у̃ = 23,15 - 0,18х. Вычислим по этому уравнению расчетные значения прибыли у̃i для каждой группы. Подставив в уравнение середины интервалов групп х̅', запишем у̃i в графу 9 табл. 8.2. Вариация расчетных значений прибыли связана с влиянием оборачиваемости х. Найдем сумму квадратов отклонений прибыли за счет вариации оборачиваемости - факторную вариацию (графа 10 табл. 8.2). Для расчета общей вариации результативного признака была вычислена сумма квадратов отклонений по индивидуальным данным: Эта сумма квадратов - общая вариация объема прибыли - равна 222,4. Теперь можем построить меры тесноты связи: теоретическое корреляционное отношение эмпирическое корреляционное отношение (рассчитанное в гл. б) Оба квадрата корреляционных отношений соответствуют по содержанию ранее рассмотренному коэффициенту детерминации (8.1) и (8.2) и интерпретируются как Показатели доли вариации результативного признака, объясняемой за счет вариации группировочного, факторного признака (и, конечно, связанных с ним прочих факторов). В данном примере связь является тесной. Различие в том, что в эмпирическом корреляционном отношении связь признаков не абстрагирована от случайных влияний прочих факторов на вариацию у, не связанных с вариацией х. Наиболее рациональным приемом анализа и расчета параметров корреляционной связи с помощью группировки является построение так называемой «корреляционной решетки» (табл. 8.3). Это таблица, в которой изучаемая совокупность сгруппирована одновременно по обоим признакам, связь между которыми изучается (двумерное распределение). Число групп по признакам может быть как равным, так и неравным. Если наибольшие числа частот каждой строки и каждого столбца располагаются на первой диагонали (в табл. 8.3 эти цифры подчеркнуты), связь является прямой и близкой к линейной; если наибольшие числа частот располагаются вдоль второй диагонали (в табл. 8.3 эти цифры также подчеркнуты), связь обратная, линейная. Если частоты во всех клетках таблицы примерно равны, связи нет; если наибольшие числа расположены по дуге, связь криволинейная. В табл. 8.3 кроме частот приведены строки и графы для расчета необходимых сумм при вычислении параметров корреляционной связи. 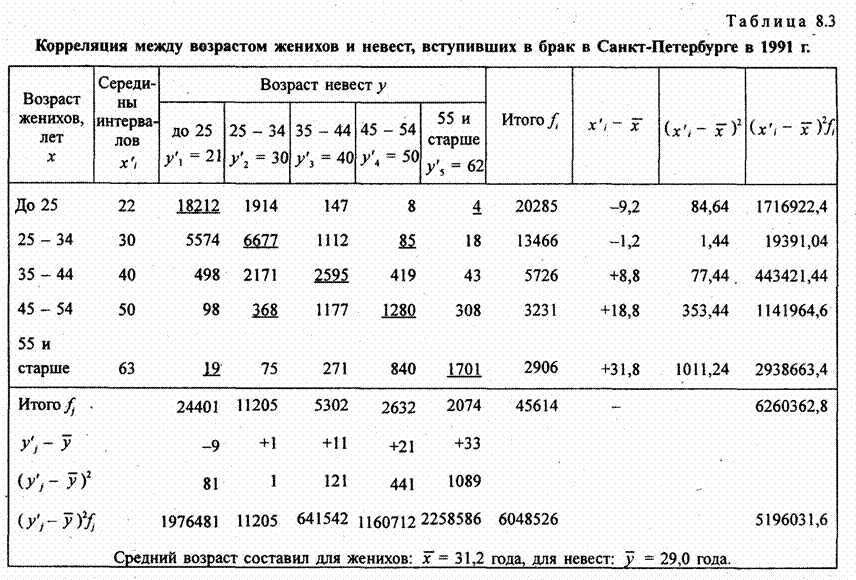
В табл. 8.3 наибольшие частоты в строках и графах расположены вдоль первой диагонали, что говорит в соответствии с логикой о прямой линейной связи возрастов женихов и невест. Связь эта далеко не полная; как видим, «любви все возрасты покорны», все клетки таблицы заполнены, значит, существуют браки между лицами любых возрастов. Как средние величины признаков, так и все суммы, входящие в расчет параметров корреляции, при группировке взвешиваются на соответствующие частоты, поэтому формулы (8.9) и (8.11) приобретают следующий вид: где x'i, yj. - середины интервалов i-й категории х и j-й категории y; fi - частота i-го значения х; fj - частота j-го значения у; fij - частота совместного появления i-го значения х и j-гo значения у (это числа в клетках «корреляционной решетки»). Взвешенные суммы квадратов отклонений подсчитаны и приведены в последней графе и в последней строке табл. 8.3. Для вычисления числителя в (8.22) и (8.23) необходимо умножить отклонения по обоим признакам (с учетом их знаков) на частоты совместного распределения и сложить все 25 произведений: (-9).(-9,2)·18212 +1·(-9,2)·1914 + ... + 33·31,8·1701 = 5196031,6. Это число записано в правом нижнем углу табл. 8.3. Рассчитаем параметры уравнения регрессии. Согласно (8.22) Это означает, что в среднем с увеличением возраста женихов на 1 год возраст их невест возрастал на 0,83 года. Свободный член уравнения согласно (8.6) a = 29,0 - 0,83·31,2 = 3,1. Уравнение имеет вид: у̂ = 3,1 + 0,83·х. Так как оба признака равноправны, то можно получить уравнение зависимости среднего возраста жениха от возраста невесты. Поменяв местами х и у, получаем:
Коэффициент корреляции согласно формуле (8.23) составляет: Коэффициент детерминации r2 = 71,3%, т. е. вариация возраста супруга или супруги на 71% зависит от вариации возраста «второй половины». Связь весьма тесная. Конечно, расчет параметров корреляции на основе группировки является приближенным: реальные значения признаков заменяются серединами интервалов, а при открытых интервалах - их экспертными оценками. Не учитывается неравномерность изменения частот внутри интервалов. Казалось бы, с появлением программ для ЭВМ этот метод должен отмереть. Однако для больших совокупностей в десятки и сотни тысяч единиц большинство программ ввиду ограничений на объем оперативной памяти непригодно. Да и сам процесс занесения в память ЭВМ сотни тысяч чисел занял бы столь громадное время, что, выигрыш во времени расчета на ЭВМ был бы многократно превышен. Таким образом, иногда трудоемкость расчета с помощью группировки и простого калькулятора оказывается намного меньше, чем на ЭВМ, а степень точности достаточна для большинства задач анализа связи. 8.8. Коэффициент корреляции ранговК мерам тесноты парной связи относится и предложенный английским психологом Ч. Спирменом (1863 - 1945) коэффициент корреляции рангов. Ранги - это порядковые номера единиц совокупности в ранжированном ряду. Если проранжировать совокупность по двум признакам, связь между которыми изучается, то полное совпадение рангов означает максимально тесную прямую связь, а полная противоположность рангов - максимально тесную обратную связь. Ранжировать оба признака необходимо в одном и том же порядке: либо от меньших значений признака к большим, либо наоборот. Если ранги единиц совокупности по признакам х и у обозначить какр^,, р ,, то коэффициент корреляции рангов согласно (8.11) имеет вид: где р̅x = р̅y - средние ранги в ряду натуральных чисел от 1 до п, равные, как известно, (п +1)/2. Также известно, что сумма квадратов отклонений чисел натурального ряда от их средней величины Рассмотрим далее разности рангов di =pxi –pyi и сумму их квадратов:
Отсюда
Это числитель коэффициента корреляции рангов. Подставив в (8.24) найденные выражения для числителя и для знаменателя, имеем:
Это и есть формула Спирмена. Преимущество коэффициента корреляции рангов состоит в том, что ранжировать можно и по таким признакам, которые нельзя выразить численно: можно проранжировать кандидатов на занятие определенной должности по профессиональному уровню, по умению руководить коллективом, по личному обаянию и т. п, При экспертных оценках можно ранжировать оценки разных экспертов и найти их корреляции друг с другом, чтобы затем исключить из рассмотрения оценки эксперта, слабо коррелированные с оценками других экспертов. Коэффициент корреляции рангов, как будет показано в гл. 9, применяется для оценки устойчивости тенденции динамики. Недостатком коэффициента корреляции рангов является то, что одинаковым разностям рангов могут соответствовать совершенно отличные разности значений признаков (в случае количественных признаков). Поэтому для последних следует считать корреляцию рангов, как и коэффициент знаков Фехнера, приближенными мерами тесноты связи, обладающими меньшей информативностью, чем коэффициент корреляции числовых значений признаков. В качестве примера рассчитаем коэффициент корреляции рангов по данным табл. 8.1 (табл. 8.4). Коэффициент корреляции рангов по формуле Спирмена
Полученное значение больше коэффициента Фехнера, но намного ниже обычного коэффициента корреляции, составившего 0,916. Как видим, недоучет размеров отклонений признаков от их средних величин занижает меру тесноты связи. Если среди значений признаков х и у встречается несколько одинаковых, образуются связанные ранги, т. е. одинаковые средние номера; например, вместо одинаковых по порядку третьего и четвертого значений признака будут два ранга по 3,5. В таком случае коэффициент Спирмена вычисляется как где: j - номера связок по порядку для признака х; Аj - число одинаковых рангов в j-й связке по х; k - номера связок по порядку для признака у; Вk — число одинаковых рангов в k-й связке по у. Таблица 8.4 Расчет коэффициента корреляции рангов по данным табл. 8.1
Коэффициент корреляции рангов может быть рассчитан и по формуле, предложенной английским статистиком М. Кендаллом:
где s - фактическая сумма рангов;
Этот коэффициент также изменяется в пределах - 1 < t < 1. Он дает несколько более строгую оценку связи нежели коэффициент Спирмена:
Это соотношение выполняется при большом числе наблюдений, п > 30, и слабых либо умеренно тесных связях. Для расчета т все единицы ранжируются по признаку х; по ряду другого признака у подсчитывается для каждого ранга число последующих рангов, превышающих данный (их сумму обозначим Р), и число последующих рангов ниже данного (их сумму обозначим Q). Тогда S = Р - Q. Можно показать, что P+Q= - n(n-1), так что t может быть представлен как Вычислим коэффициент корреляции рангов Кендалла по данным табл. 8.4:
отношение между этими двумя коэффициентами не вполне соответствует упомянутому: коэффициент Спирмена в нашем примере превосходит t не в 1,5 раза, а на 23%. 8.9. Параболическая корреляцияЛинейные связи являются основными. Однако встречаются и нелинейные связи, хорошо описываемые параболой, гиперболой и т. д. Уравнение регрессии в форме параболы 2-го порядка имеет следующий вид:
Если при линейной связи среднее изменение результативного признака на единицу фактора постоянно по всей области вариации фактора, то при параболической корреляции изменение признака х на единицу признака^ меняется равномерно с изменением величины фактора. В результате связь может даже поменять знак на противоположный, из прямой превратится в обратную, из обратной в прямую. Такой характер связи объективно присущ многим системам. Например, с увеличением дозы удобрений урожайность сель-хозкультур сначала повышается, но если превысить оптимальную величину дозы, то при дальнейшем росте дозы удобрений растения угнетаются и урожайность снижается. Нормальные уравнения метода наименьших квадратов для параболы 2-го порядка таковы:
Если расчет производится не по индивидуальным данным, а на основе аналитической группировки, то уравнения МНК приобретают следующий вид:
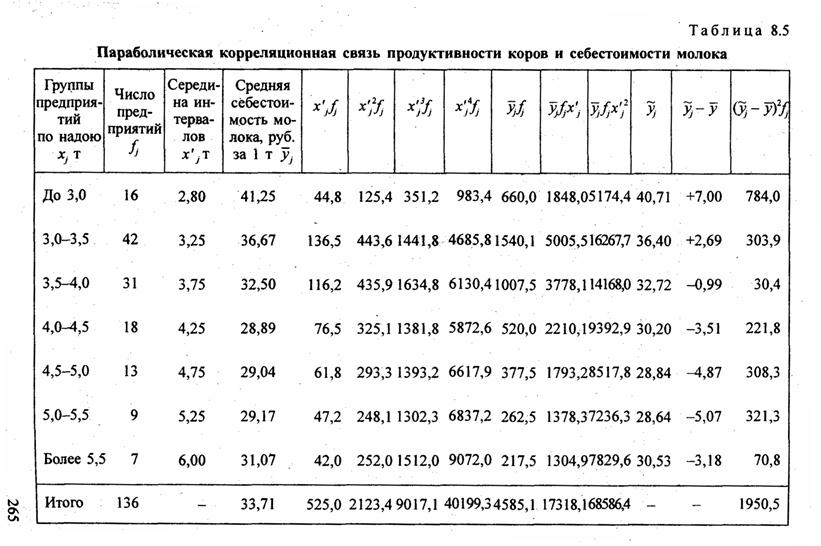
Решая эту систему, получаем значения параметров а, b и с. Показателем тесноты параболической корреляции является корреляционное отношение, вычисляемое как корень квадратный из выражения (8.2). В качестве примера параболической корреляционной связи рассмотрим зависимость себестоимости молока от продуктивности коров по данным аналитической группировки сельхозпредприятий области (табл. 8.5). В этой же таблице приведены расчетные величины, входящие в уравнения МНК для параболы. Были получены нормальные уравнения МНК: 136а + 5256 + 2123,4с = 4585,1, 525а+2123.4А + 9017,1с = 17318,1, 2123,4а + 9017,16 + 40199,3с = 68586,4.
Эта парабола имеет точку минимума в фактической области вариации факторного признака. Для нахождения значения фактора, при котором достигается минимальное значение результативного признака, следует приравнять нулю первую производную по х уравнения (8.30):
откуда х = 23,641/4,6498 = 5,084 т молока на корову. Итак, минимальная себестоимость молока в совокупности предприятий, в условиях периода, к моторому относятся данные, достигалась в среднем при надое молока на корову 5084 кг. Значение фактора х при достижении минимума себестоимости можно назвать оптимальной продуктивностью коров, а сама задача его поиска - это одна из оптимизационных задач, решаемая математико-статистическим методом.
Для измерения тесноты параболической корреляционной связи находим вариацию результативного признака у, объясняемую вариацией фактора х как сумму квадратов отклонений расчетных величин у от средней величины у, взвешенных на число предприятий. Общая сумма квадратов отклонений всех 136 значений у, от средней величины составляет 4624,7. Таким образом согласно формуле (8.1), корреляционное отношение
8.10. Гиперболическая корреляцияУравнение регрессии в форме гиперболы имеет следующий вид:
Если величина Ъ положительна, то при увеличении значений факторного признака х значения результативного признака уменьшаются, причем это уменьшение все время замедляется, и при х -> оо средняя величина признака у будет равна а. Если же параметр Ь отрицателен, то значения результативного признака с ростом фактора возрастают, причем- их рост замедляется, и в пределе при х ® ¥ у̃ = а. Таким образом, гиперболические зависимости характерны для связей, в которых результативный признак не может варьировать неограниченно, его вариация имеет односторонний предел. Например, при освоении нового оборудования его производительность возрастет, но рост замедлится по мере приближения к конструктивно-технологическому пределу производственной мощности агрегата. Совершенствуя двигатель, можно увеличивать его КПД, но тоже не выше предела, допускаемого данным видом преобразования энергии. Таков же характер связи между уровнем душевого дохода х в семье и долей семей, имеющих телевизоры, у; он приближен к пределу (100%) в наиболее обеспеченной группе семей. Нормальные уравнения метода наименьших квадратов для гиперболы таковы:
Легко видеть, что эти уравнения, по существу, те же, что и для линейной связи. Линеаризация гиперболического уравнения достигается заменой 1/х на новую переменную, которую можно обозначить z. Тогда уравнение (8.27) примет вид ỹ = а + bz. Это и следует cделать, вычисляя гиперболу на компьютере, если программа для него не предусматривает автоматического вычисления гиперболических регрессий. В качестве примера расчета уравнения гиперболической связи рассмотрим влияние среднесуточного прироста живой массы крупного рогатого скота на откорме на себестоимость прироста живой массы в совокупности предприятий области, занимавшихся откормом скота (табл. 8.6).
где х в сотнях граммов Таблиц а 8.6 Гиперболическая связь себестоимости прироста со скоростью прироста массы скота
Точечный прогноз по уравнению регрессии при среднесуточном приросте массы животных, равном 900 г, уже достигнутом передовыми хозяйствами, приводит к ожидаемой средней себестоимости.
Следовательно, 67% вариации себестоимости прироста массы скота объяснились вариацией скорости роста массы животных и связанных с ней других факторов, например, чем быстрее растет масса, тем меньше расход кормов на единицу прироста массы. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

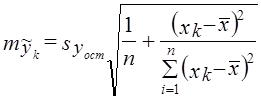 , (8.20)
, (8.20)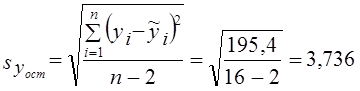 ц на одну корову
ц на одну корову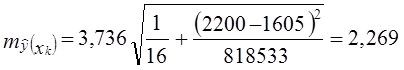 ц на 1 корову.
ц на 1 корову.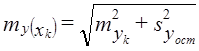 . (8.21)
. (8.21)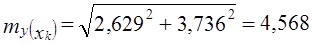 ц на 1 корову.
ц на 1 корову.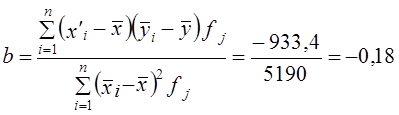 ,
,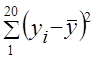 .
.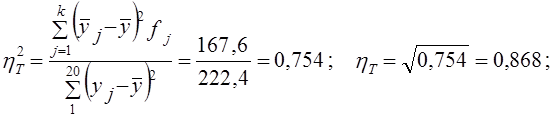
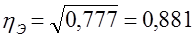 .
.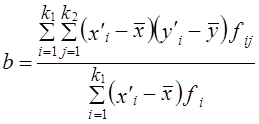 , (8.22)
, (8.22)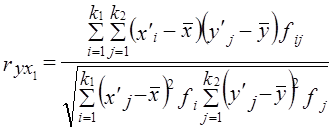 , (8.23)
, (8.23) 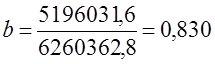
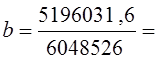 =0,859; а = 31,2 - 0,859·29 = 6,3; х̂ = 6,3 + 0,859у.
=0,859; а = 31,2 - 0,859·29 = 6,3; х̂ = 6,3 + 0,859у.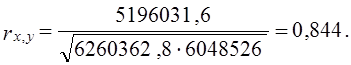
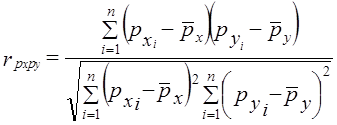 , (8.24)
, (8.24)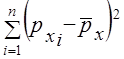 и
и 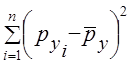 равна (n3 - n)/12. Следовательно, знаменатель формулы (8.23) есть (п3 - п)/12.
равна (n3 - n)/12. Следовательно, знаменатель формулы (8.23) есть (п3 - п)/12.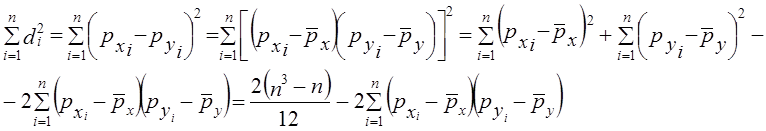
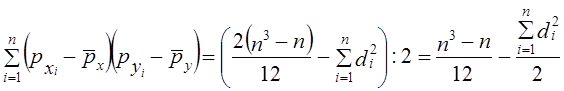
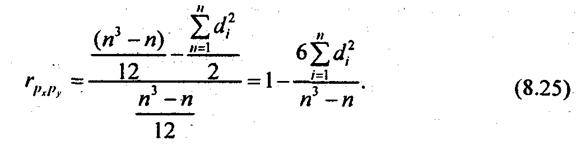
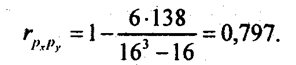
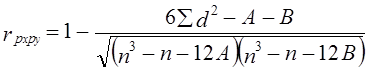 , (8.26)
, (8.26)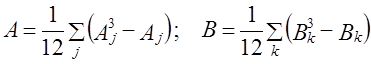 ;
;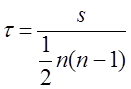 , (8.27)
, (8.27)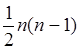 - максимальная сумма рангов.
- максимальная сумма рангов.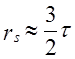 .
.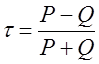 (8.28)
(8.28)