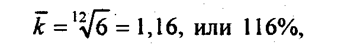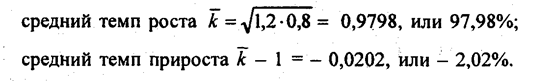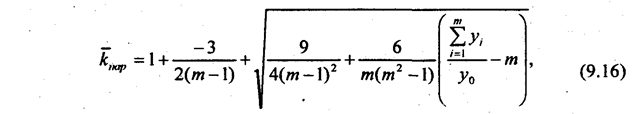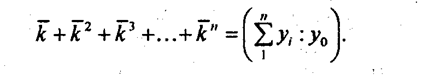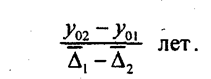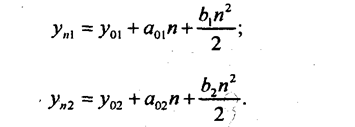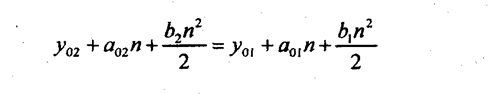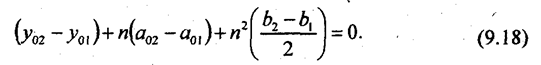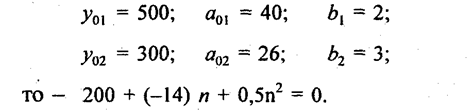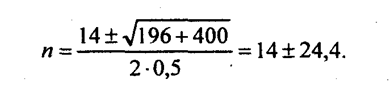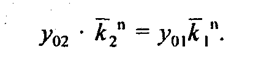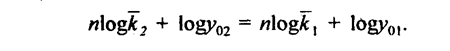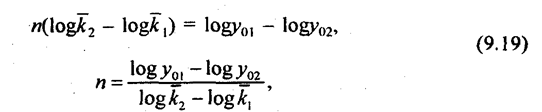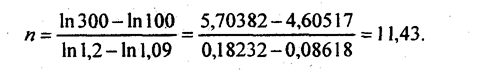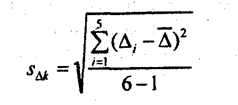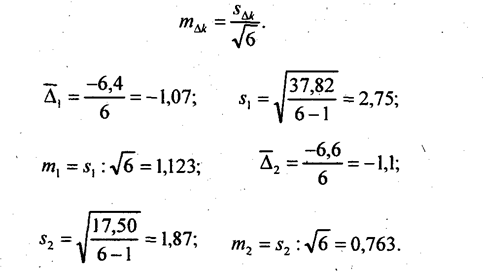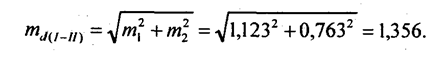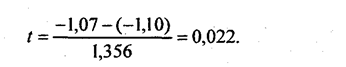| Главная » Учебно-методические материалы » СТАТИСТИКА » Общая теория статистики: учебник. Под ред. Елисеевой И.И. |
| 23.01.2012, 17:22 | ||||||||||||||||||||||||||||||||
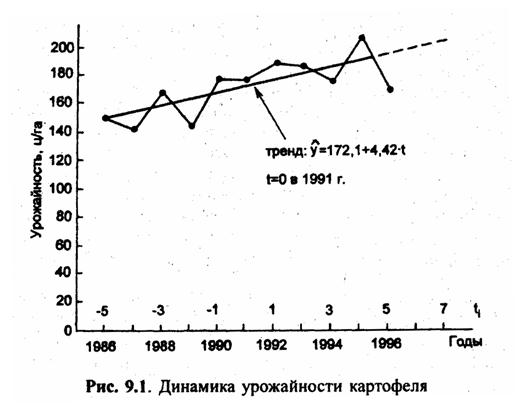
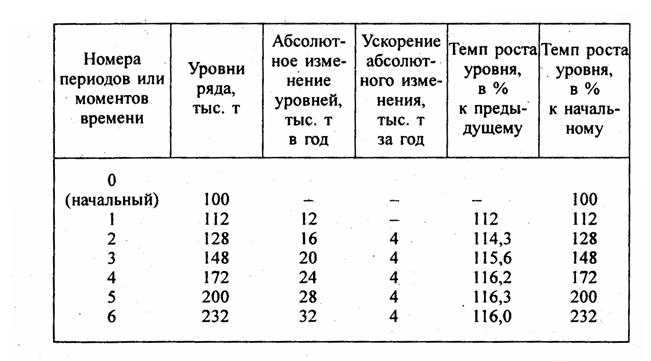
| Одно из основных положений научной методологии - необходимость изучать все явления в развитии, во времени. Это относится и к статистике: она должна дать характеристику изменений статистических показателей во времени. Как изменяются год за годом валовой национальный продукт и национальный доход страны? Как возрастает или снижается уровень оплаты труда? Велики ли колебания урожайности зерновых культур и существует ли тенденция ее роста? На все аналогичные вопросы ответ может дать только специальная система статистических методов, предназначенная для изучения развития, изменений во времени или, как принято в статистике говорить, изучения динамики. 9.1. Составляющие элементы динамики: основная тенденция и колебанияРассмотрим данные табл. 9.1. Условимся, что относящиеся к отдельным годам значения урожайности картофеля, будем называть уровнями, а всю их последовательность с 1986 по 1996 г. -рядом динамики (динамическим рядом, временным рядом, английский термин «Time series»). Таблица 9.1 Динамика урожайности картофеля в хозяйстве Ряд динамики состоит из двух строк или столбцов: промежутков или моментов времени, к которым относятся уровни, и самих уровней признака (показателя). Ряд, в котором время задано в виде промежутков - лет, месяцев, суток, называется интервальным динамическим рядом. В табл. 9.1 приведен такой ряд. Ряд, в котором время задано в виде конкретных дат (моментов времени), называется моментным динамическим рядом. Например, ряд численности населения по оценке на 1 января каждого года. Вернемся к табл. 9.1. Сравнивая уровни разных лет, мы замечаем, что в целом урожайность возрастает. Однако нередко уровень урожайности следующего года оказывается ниже предыдущего. Иногда рост по сравнению с предыдущим годом велик, как в 1990 г., а иногда мал. Следовательно, рост урожайности наблюдается лишь в среднем, как тенденция. В отдельные же годы уровни испытывают колебания, отклоняясь от основной тенденции. Эти колебания урожайности связаны в основном с различием метеорологических . условий в разные годы. Если рассматривать динамические ряды месячных уровней производства мяса или молока, ряды объема продажи разных видов одежды и обуви, ряды заболеваемости населения, выявятся регулярно повторяющиеся из года в год сезонные колебания уровней. В силу солнечно-земных связей частота полярных сияний, интенсивность гроз, те же изменения урожайности отдельных сельхозкуль-тур и ряд других процессов имеют циклическую 10 - 11- летнюю колеблемость. Колебания числа рождений, связанные с потерями в войне, повторяются с угасающей амплитудой через поколение, т.е. через 20 - 25 лет. Тенденция динамики связана с действием долговременно существующих причин и условий развития, хотя, конечно, после какого-то периода эти причины и условия тоже могут измениться и породить уже другую тенденцию развития изучаемого объекта. Колебания же, напротив, связаны с действием краткосрочных или циклических факторов, влияющих на отдельные уровни динамического ряда, и отклоняющих уровни от тенденции то в одном, то в другом направлении. Например, тенденция динамики урожайности связана с прогрессом агротехники, с укреплением экономики данной совокупности хозяйств, совершенствованием организации производства. Колеблемость урожайности вызвана чередованием благоприятных по погоде и неблагоприятных лет, циклами солнечной активности, колебаниями в развитии вредных насекомых и болезней растений. При статистическом изучении динамики необходимо четко разделить ее два основных элемента - тенденцию и колеблемость чтобы дйть каждому из них количественную характеристику с по^ мощыо специальных показателей. Смешение тенденции и колеблемости ведет к неверным выводам о динамике. Если из табл. 9.1 произвольно взять данные за отдельные годы и сравнить их друг с другом, можно получить «выводы», прямо противоположные истине. Например, если сравнить урожайность в 1995 г. с урожайностью в 1987 г., то получим, что за 8 лет она возросла на 66 ц с 1 га, т.е. более чем по 8 ц с 1 га за год. Если же урожайность в 1996 г. сравнить с ее уровнем в 1988 г., то получим, что за 8 лет, из которых 7 лет те же, что и в предыдущем сравнении, урожайность возросла всего лишь на 2 ц с1 га. Тенденцию и колебания наглядно показывает график (рис. 9.1). По оси абсцисс всегда отражается время, по оси ординат - уровни. По обеим осям строго соблюдается масштаб, иначе характер динамики будет искажен. На рис 9.1 хорошо заметно, что рост урожайности в 1986 - 1996 гг. характеризовался линейной тенденцией, а колеблемость была хаотической, без явной цикличности. О линии тренда и ее уравнении будет сказано далее, в п. 9.5 и 9.6. 9.2. Показатели, характеризующие тенденцию динамикиЧтобы построить систему показателей, характеризующих тенденцию динамики, нужно ответить на вопрос: какие черты, свойства этой тенденции нужно измерить и выразить в статистических показателях? Очевидно, нас интересует величина изменений уровня как в абсолютном, так и в относительном выражении (на какую долю, процент уровня, принятого за базу, произошло изменение?). Далее нас интересует: является ли изменение равномерным или неравномерным, ускоренным (замедленным?). Наконец, нас интересует выражение тенденции в форме некоторого достаточно простого уравнения, наилучшим образом аппроксимирующего фактическую тенденцию динамики. Понятие об уравнении тенденции динамики было введено в статистику английским ученым Гукером в 1902 г. Он предложил называть такое уравнение трендом (the trend). Для того чтобы нагляднее представить показатели, характеризующие тенденцию, следует абстрагироваться от колеблемости и выявить динамический ряд в форме «чистого» тренда при отсутствии колебаний. Пример такого ряда представлен в табл. 9.2. Таблица 9.2 Абсолютные и относительные показатели тенденции
Абсолютное изменение уровней - в данном случае его можно назвать абсолютным приростом - это разность между сравниваемым уровнем и уровнем более раннего периода, принятым за базу сравнения. Если эта база непосредственно предыдущий уровень, показатель называют цепным, если за базу взят, например, начальный уровень, показатель называют базисным. Формулы абсолютного изменения уровня:
Если абсолютное изменение отрицательно, его следует называть абсолютным сокращением. Абсолютное изменение имеет ту же единицу измерения, что и уровни ряда с добавлением единицы времени, за которую определено изменение: 22 тысячи тонн в год (или 1,83 тыс. т в месяц, или 110 тыс. т в пятилетие). Без указания единицы времени, за которую произошло измерение, абсолютный прирост нельзя правильно интерпретировать. В табл. 9.2 абсолютное изменение уровня не является константой тенденции. Оно со временем возрастает, т.е. уровни ряда изменяются с ускорением. Ускорение - это разность между абсолютным изменением за данный период и абсолютным изменением за предыдущий период одинаковой длительности:
Показатель абсолютного ускорения применяется только в цепном варианте, но не в базисном. Отрицательная величина ускорения говорит о замедлении роста или об ускорении снижения уровней ряда. Как видно по данным табл. 9.2, ускорение является константой тенденции данного ряда, что свидетельствует о параболической форме этой тенденции. Ее уравнение имеет вид:
Показатель ускорения абсолютного изменения уровней выражается в единицах измерения уровня, деленных на квадрат длины периода. В нашем случае ускорение составило 4 тыс. т в год за год или 4 тыс. т год-2. Смысл показателя следующий: объем производства (или добычи угля, руды) имел абсолютный прирост, возрастающий на 4 тыс. т в год ежегодно. Усвоить рассмотренные показатели поможет следующая аналогия с механическим движением: уровень - это аналог пройденного пути, причем начало его отсчета не в нулевой точке. Абсолютный прирост - аналог скорости движения тела, а ускорение абсолютного прироста - аналог ускорения движения. Пройденный путь, считая и тот, который уже был пройден до начала отсчета времени в данной задаче, равен:
Сравнивая с формулой (9.3), видим, что s0 - аналог свободного члена a, v0 - аналог абсолютного изменения в; a/2 — аналог ускорения прироста С. Как показано в гл. 3, система показателей должна содержать не только абсолютные, но и относительные статистические показатели. Относительные показатели динамики необходимы для сравнения развития разных объектов, особенно если их абсолютные характеристики различны. Предположим, другое предприятие увеличивало производство аналогичной продукции с тенденцией, выраженной уравнением тренда: уi = 20 + 4t + 0,5t2i. И абсолютный прирост, и ускорение роста объема продукции во втором предприятии гораздо меньше, чем в первом. Но можно ли ограничиться этими показателями и сделать вывод, что развитие второго предприятия более медленное, чем первого? Меньший уровень еще не есть меньший темп развития, и это покажет относительная характеристика тенденции динамики — темп роста. Темп роста — это отношение сравниваемого уровня (более позднего) к уровню, принятому за базу сравнения (более раннему). Темп роста исчисляется в цепном варианте - к уровню предыдущего года и в базисном варианте — к одному и тому же, обычно начальному уровню (см. формулы (9.4). Он говорит о том, сколько процентов составляет сравниваемый уровень по отношению к уровню, принятому за базу, или во сколько раз сравниваемый уровень больше уровня, принятого за базу. При этом если уровни снижаются со временем, то сказать, что последующий уровень «больше в 0,33 раза», или составляет 33,3% базового уровня, это, разумеется, означает, что уровень уменьшился в 3 раза. Но сказать что «уровень меньше в 0,33 раза», это неверно. Темп изменения в разах всегда говорит о том, во сколько раз сравниваемый уровень больше. Теперь можно сказать, что относительная характеристика роста объема продукции на первом предприятии в среднем за год близка к 115% (рост приблизительно на 15% за год), и за шесть лет продукция увеличилась в 2,32 раза, а на втором предприятии, вычислив также шесть уровней параболического тренда, читатель убедится, что в среднем за год объем продукции возрастал примерно на 20%, а за шесть лет объем ее возрос в 3,1 раза. Следовательно, в относительном выражении объем продукции на втором предприятии развивался, возрастал быстрее. Только в сочетании абсолютных и относительных характеристик динамики можно правильно отразить процесс развития совокупности (объекта).
или же темпом прироста. Он равен к-\ или к-100%. Темп прироста (относительное изменение) может иметь как положительные значения, так и отрицательные. Наоборот, темп изменения -величина всегда положительная. Если уровень ряда динамики принимает положительные и отрицательные значения, например финансовый результат от реализации продукции предприятием может быть прибылью (+), а может быть убытком (-), тогда темп изменения и темп прироста применять нельзя. В этом случае такие показатели теряют смысл и не имеют экономической интерпретации. Сохраняют смысл только абсолютные показатели динамики. Рассмотрим соотношения между цепными и базисными показателями на примере данных табл. 9.2: 1) сумма цепных абсолютных изменений равна базисному абсолютному изменению SDi(цепн) = Di(баз). (9.6) По данным табл. 9.2 получим: 12 + 16 + 20 + 24 + 28 + 32 = 232 - 100 = 132; 2) произведение цепных темпов изменения равно базисному темпу изменения По данным табл. 9.2 получим: 1,12·1,143·1,156·1,162·1,163·1,16 = 2,32. Сумма цепных темпов прироста не равна базисному темпу прироста. 12 + 13,3 + 15,6 + 16,2 + 16,3 + 16 ≠ 132 (в процентах). Значения цепных темпов прироста, рассчитанных каждый к своей базе, различаются не только числом процентов, но и величиной абсолютного изменения, составляющей каждый процент. Поэтому складывать или вычитать цепные темпы прироста нельзя. Абсолютное значение 1% прироста равно сотой части предыдущего уровня, или базисного уровня. 9.3. Особенности показателей динамики для рядов, состоящих их относительных уровнейУровнями динамического ряда могут быть не только абсолютные показатели. Ряды динамики могут отражать развитие структуры совокупности, изменение со временем вариации признака в совокупности, взаимосвязи между признаками, соотношения значений признака для разных объектов. В этих случаях уровни динамического ряда сами являются относительными показателями, нередко выражаются в процентах. Следовательно, абсолютные изменения (и ускорения) тоже окажутся относительными величинами, могут быть выражены в процентах. В процентах, разумеется, будут выражены темпы изменения и относительные приросты. Все это создает нередко путаницу в интерпретации и использовании показателей динамики в печати и даже в специальной экономической литературе. Рассмотрим пример. В США с конца XIX в. для группы ведущих акционерных компаний исчисляется так называемый индекс Доу Джонса - арифметическая средняя величина котировок акций на фондовых биржах. Этот показатель характеризует хозяйственную конъюнктуру: если индекс Доу Джонса повышается, т.е. растет относительная цена акций, значит, вкладчики капитала рассчитывают получить по акциям больший дивиденд (распределяемая часть прибыли). Это говорит о росте деловой активности. Падение индекса Доу Джонса говорит о снижении деловой активности в стране. Величина этого показателя есть отношение в процентах цены акций на бирже к их номиналу (первоначальной цене при выпуске акций). Это отношение зависит не только от колебаний деловой активности, но имеет также общую тенденцию роста ввиду инфляции - падения покупательной силы доллара США. С начала века этот рост значителен, поэтому в наше время индекс Доу Джонса составляет более 2000% (акция, когда-то выпущенная на сумму 100 долл., теперь стоит более 2000 современных долларов). Биржевые новости за 5.05.1990 г. сообщают: индекс Доу Джонса на 3.05.1990 г. составил 2689,64% в сравнении с 2759,55% на 29.04.1990 т. Если вычислить показатель абсолютного изменения индекса, т.е. 2689,64% - 2759,55% =- 69,91%, и сказать, что индекс Доу Джонса за неделю понизился почти на 70%, создается ложное впечатление о чудовищном крахе на биржах США, потому что снижение на 70% воспринимается как темп изменения - будто от прежней цены акций осталось только 30%. На самом деле снижение показателей с 2760 до 2690% никакой катастрофой экономике США не грозит: это обычная на рынке ценных бумаг колеблемость курсов. «Биржевые ведомости» далее сообщали, что индекс Доу Джонса на 7.06.1990 г. достиг 2911,6%, т.е. с 5.05.1990 г. возрос на 222 единицы, которые во избежании путаницы принято именовать «пунктами». В первом рассмотренном случае индекс снизился на 70 пунктов, во втором - возрос на 222 пункта, а не процента. В процентах рост составил: 222 : 2690 = 8,25% - это и есть темп прироста курса акций. Аналогичные термины должны, применяться и к динамике показателей структуры. Например, общее производство электроэнергии в Российской Федерации в 1980 г. составляло 805 млрд кВ-ч, в том числе на атомных электростанциях 54 млрд кВт-ч, т. е. их доля была равна 6,7%. В 1995 г. общее производство электроэнергии составило 860 млрд кВт-ч, в том числе на АЭС 99,5 млрд кВт-ч, или 11,6%. Доля АЭС возросла, за 15 лет на 11,6- 6,7 = 4,9 пункта. А темп роста доли АЭС составил 11,6% : 6,7% = 1,73. Доля АЭС возросла на 73%. Показатели динамики долей имеют еще одну особенность, вытекающую из того, что сумма всех долей в любой период времени равна единице, или 100%. Изменение, произошедшее с одной из долей, поэтому, неизбежно меняет и доли всех других частей целого, если даже по абсолютной величине эти части не изменились. Казалось бы, это положение самоочевидно, однако нередко в печати встречаются рассуждения о том, что увеличение доли пшеницы и ячменя среди зерновых культур - это хорошо, но вот плохо, что уменьшились доли ржи, овса и гречихи. Как будто все доли сразу могут увеличиться! Если признак варьирует альтернативно, то увеличение доли одной группы равно уменьшению доли другой группы в пунктах, но темпы изменения долей в процентах при этом могут сильно различаться. Темп больше у той доли, которая в базисном периоде была меньше - темп прироста (изменения) понимается по абсолютной величине, по модулю. Например, в 1992 г. оплата труда составила 69,9% всех денежных доходов населения России, а прочие доходы 30,1%. В 1995 г. оплата труда составила только 39,3% всех денежных доходов населения, а доля прочих доходов возросла до 60,7%. Темп прироста доли прочих доходов составил 201,7%, т. е. их доля возросла на 101,7%. Доля же оплаты труда сократилась в относительном выражении на 43,8% В общем виде темп роста одной из альтернативных долей зависит от темпа роста другой доли и величины этой доли следующим образом:
Абсолютное изменение долей в пунктах зависит от величины доли и темпа роста таким образом:
При наличии в совокупности не двух, а более групп абсолютное изменение каждой из долей в пунктах зависит от доли этой группы в базисный период и от соотношения темпа роста абсолютной величины объемного признака этой группы со средним темпом роста объемного признака во всей совокупности. Доля f-й группы в сравниваемый (текущий) период определяется как
Рассмотрим распределение занятого населения России по секторам экономики и его изменение (табл. 9.3). Таблица 9.3 Занятое население России по секторам экономики в организациях по формам собственности1
Согласно формуле (9.10) доля работающих в организациях с государственной и муниципальной формами собственности в 1995 г. составит:
или 37,45%. Доля работающих в частном секторе: Доля работающих в общественных организациях: Доля работающих в совместных и предприятиях смешанной формы собственности:
Знаменатели обеих дробей - 0,9327 - это средний (общий) темп изменения численности всех занятых. Особенностью показателей динамики относительных величин интенсивности является то, что темпы роста и темпы прироста (или сокращения) прямого и обратного показателей не совпадают. Пример. Трудоемкость производственной операции на старом станке составляла 10 мин., а производительность труда - 48 операций за смену. После замены станка на новый трудоемкость операции снизилась в 5 раз (до 2 мин.), а производительность возросла в те же 5 раз - до 240 операций за смену. Относительное изменение трудоемкости составило (2 - 10) : 10 = -0,8, т. е. трудоемкость снизилась на 80%. Относительное изменение производительности труда составило (240 - 48) : 48 = 4 или 400%, т. е. производительность труда возросла на 400%. Причина состоит в том, что пределом, к которому стремятся по мере прогресса показатели ресурсо-отдачи, является бесконечность, а пределом, к которому стремятся обратные им показатели ресурсоемкости, является нуль. Понимание разного поведения показателей динамики прямых и обратных мер эффективности очень важно для экономиста и статистика. По мере приближения относительного показателя к пределу одно и то же абсолютное изменение в пунктах приобретает иное качественное содержание. Например, если показатель тесноты связи -коэффициент детерминации - возрос с 40 до 65% (на 25 пунктов), то система факторов в регрессионном уравнении как была, так и осталась неполной, хорошей модели не получено. Но если после изменения состава факторов коэффициент детерминации возрос с 65 до 90% - на те же 25 пунктов, это изменение имеет другое качественное содержание: получена хорошая регрессионная модель, в основном объясняющая вариацию результативного признака с достаточно полной системой факторов. 9.4. Средние показатели тенденции динамикиСредние показатели динамики - средний уровень ряда, средние абсолютные изменения и ускорения, средние темпы роста - характеризуют тенденцию. Они необходимы при обобщении характеристик тенденции за длительный период, по различным периодам и незаменимы при сравнении развития за неодинаковые по длительности отрезки времени, при выборе аналитического выражения тренда. При наличии в динамическом ряду существенных колебаний уровней определение средних показателей тенденции требует применения специальных методов статистики, которые излагаются в последующих разделах. В данном разделе рассматривается только форма, математические свойства средних показателей динамики и простейшие приемы их вычисления, применимые на практике к рядам со слабой колеблемостью. Средний уровень интервального ряда динамики определяется как простая арифметическая средняя из уровней за равные промежутки времени:
или как взвешенная арифметическая средняя из уровней за неравные промежутки времени, длительность которых и является весами. - По данным табл. 9.1 определим среднегодовые уровни урожайности картофеля по пяти-шестилетиям:
Средние уровни принято условно относить к середине интервала времени, т. е. для пятилетия 1986—1990 гг. - к 1988 г., для шестилетия 1991-1996 - к середине между 1993 и 1994 гг., т. е. к 1993,5. Если, например, с 1-го числа месяца по 18-е число на предприятии работали 45 человек, с 19-го по 27-е - 48 человек, а с 28-го по 31 -е число - 54 человека, то среднее списочное число работников за месяц составит:
В моментном ряду роль, смысл среднего уровня в том, что он характеризует уже не состояние объекта в отдельные моменты, а его среднее, обобщенное состояние между начальным и конечным моментом учета. Из этого следует, что роль уровней, отно-t сящихся к начальному и конечному моменту, существенно иная, чем роль уровней на моменты внутри изучаемого отрезка времени. Начальный и конечный уровни находятся на границе изучаемого интервала, они наполовину относятся к предыдущему и последующему интервалам и лишь наполовину к изучаемому. Уровни, относящиеся к моментам внутри осредняемого интервала, целиком относятся только к нему. Отсюда получаем особую форму средней арифметической величины, называемой хронологической средней:
Проблема вычисления среднего уровня моментного ряда при неравных промежутках между моментами является спорной и здесь не рассматривается. Если известны точные даты изменения уровней моментного ряда то средний уровень определяется как
где ti - время, в течение которого сохранялся уровень. Средний абсолютный прирост (абсолютное изменение) определяется как простая арифметическая средняя из абсолютных изменений за равные промежутки времени (цепных абсолютных изменений) или как частное от деления базисного абсолютного изменения на число осредняемых отрезков времени от базисного до сравниваемого периода:
Как уже сказано в п. 9.1, при наличии существенной колеблемости уровней средний абсолютный прирост (изменение), как и средний темп следует вычислять, отделив сначала тренд от колебаний (соответствующая методика будет изложена ниже). Прямое определение среднего абсолютного прироста по крайним уровням ряда допустимо, если нет существенных колебаний уровней. Например, добыча угля в России довольно равномерно снижалась с 337 млн т в 1992 г. до 262 млн т в 1995 г. По формуле (9.14) среднее годовое сокращение добычи угля составило: Для правильной интерпретации показатель среднего абсолютного изменения должен сопровождаться указанием двух единиц времени: 1) время, за которое он вычислен, к которому относится и которое он характеризует (в нашем примере это трехлетие - 1992 - 1995); 2) время, на которое показатель рассчитан, время, входящее в его единицу измерения, - 1 год. Можно рассчитать среднемесячный прирост за пятилетие, среднесуточное изменение за год, за месяц, за квартал. Среднее ускорение абсолютного изменения применяется реже. Для его надежного расчета даже при слабых колебаниях уровней требуется применять методику аналитического выравнивания по параболе II порядка (см. п. 9.5 и 9.6). Не рекомендуется измерять среднее ускорение без абстрагирования от колебаний уровней. Для более грубого, приближенного расчета среднего ускорения можно воспользоваться средними годовыми уровнями, сглаживающими колебания. Например, среднегодовое производство мяса в Российской Федерации составляло: Годы 1976 - 1980 1981 - 1985 1986 - 1990 Млн т 7,40 8,09 9,68 Абсолютный прирост за второе пятилетие в сравнении с первым составил 0,69 млн т, за третье в сравнении со вторым - 1,59 млн т. Следовательно, ускорение в третьем пятилетии по сравнению со вторым составило 1,59 - 0,69 = 0,90 млн т в год за пять лет, а среднегодовое ускорение прироста равно: 0,90 : 5 = 0,18 млн т в год за год. Среднее ускорение требует указания трех единиц времени, хотя, как правило, две из них одинаковы: период, на который рассчитан прирост, и время, на которое рассчитано ускорение. Средний темп изменения определяется наиболее точно при аналитическом выравнивании динамического ряда по экспоненте (см. п. 9.5 и 9.6). Если можно пренебречь колеблемостью, то средний темп определяют как геометрическую среднюю (см. гл. 5) из цепных темпов роста за п лет или из общего (базисного) темпа роста за п лет:
Например, стоимость потребительской корзины за год в результате инфляции возросла в 6 раз. Каков средний месячный темп инфляции?
т.е. в среднем за месяц цена увеличивалась на 16% к уровню предыдущего месяца. Средний темп роста так же, как средний прирост, следует сопровождать указанием двух единиц времени: 1) периода, который им характеризуется; 2) периода, на который рассчитан темп. Например, среднегодовой темп за последнее десятилетие; среднемесячный темп за полугодие и т.п. Если исходной информацией служат темпы прироста и нужно вычислить их среднегодовую величину, то предварительно следует все темпы прироста превратить в темпы роста, прибавив 1, или 100%, вычислить их среднюю геометрическую и снова вычесть 1, или 100%. Интересно, что ввиду асимметрии темпа прироста и темпа сокращения при равных их величинах общий темп прироста всегда отрицателен. Так, если за первый год объем производства вырос на 20%, а за второй снизился на 20% (темпы цепные), то за два года имеем:
Как отмечалось в главе 5, применяя для вычисления среднего темпа среднюю геометрическую, мы опираемся на соблюдение фактического отношение конечного уровня к начальному при замене фактических темпов на средние. В практических задачах может потребоваться вычисление среднего уровня при условии соблюдения отношения суммы уровней за период к уровню, принятому за базу. Например, если общий выпуск продукции за пятилетие должен составить 800% к базисному (среднегодовому за предыдущие 5 лет выпуску), или, что то же самое, среднегодовой уровень должен составить 160% к базовому уровню, каков должен быть среднегодовой темп роста выпуска продукции? В 1974 г. украинские статистики А. и И. Соляники предложили следующую приближенную формулу для среднего темпа роста, удовлетворяющую этому условию:
где т - число суммируемых уровней; у0 - базисный уровень.
Расчет по этому среднегодовому темпу дает сумму выпуска за 5 лет в 8,069 раза больше базисной, т.е. приближение хорошее. В общем виде проблема параболических темпов исследована саратовским статистиком Л. С. Казинцом в книге «Темпы роста и абсолютные приросты» (М.: Статистика, 1975). Им составлены таблицы, с помощью которых, зная отношение суммы уровней к базисному уровню и число суммируемых уровней т, можно получить knap. Таблица Л. С. Казинца рассчитана на основе нахождения корней уравнения:
Для нашего примера таблица Л. С. Казинца дает среднегодовой темп роста 116,1% и сумму выпуска в 8,00016 раза больше базисной. Если необходимо определить средний темп изменения, исходя из заданной на п периодов суммы абсолютных изменений, то следует использовать формулу (9.17):
Интересную задачу представляет определение срока, за который ряд с большим средним показателем динамики, но меньшим начальным уровнем догонит другой ряд с большим начальным уровнем, но меньшим показателем динамики.
Та же задача может быть решена на основе ускорений. Имеем первый ряд с базисным уровнем у01, базисным абсолютным изменением a01 и средним ускорением b1; второй ряд - с показателями у02, а02, b02. При каком числе п периодов (лет) после базисного уровня рядов сравняются? Тенденции рядов параболические:
Приравняв правые части уравнений, получим:
или
Искомый срок п является корнем этого квадратного уравнения. Если, например, имеем:
Откуда
Второй ряд догонит первый по уровню через 38,4 года; в прошлом уровни рядов были одинаковы 10,4 года назад. Будущие равные уровни составляют 3510, а прошлые были равны 192. Если мы хотим найти срок п, через который уровни рядов сравняются, то эту задачу можно решить и на основе средних темпов динамики. Имеем:
Логарифмируя это равенство получаем:
т. е. искомый срок равен частному от деления разности логарифмов уровней рядов в базисном периоде на разность логарифмов темпов изменения, только переставленных при вычитании. Обычно и в числителе, и в знаменателе от большего логарифма вычитается меньший. Например, первый ряд имеет у10 = 300; k1 =1,09; второй ряд имеет у110 100; k11 = 1,2. Тогда:
Через 11,43 года уровень второго ряда сравняется с первым при сохранении экспоненциальных трендов обоих рядов. 9.5. Методы выявления типа тенденции динамикиПрежде чем применить методы математического анализа для вычисления параметров уравнения тренда, необходимо выявить тип тенденции, а эта задача не является чисто математической. Наличие колебаний уровней крайне усложняет выявление типа тенденции и требует всестороннего подхода к этой проблеме, прежде всего качественного изучения характера развития объекта. При этом нужно дать ответ на такие вопросы: 1. Были ли условия развития объекта достаточно однородными в изучаемый период? 2. Каков характер действия основных факторов развития? 3. Не произошло ли качественное, существенное изменение условий развития объекта внутри изучаемого периода времени? Если, например, часть периода предприятие работало по старой технологии, а затем произошло техническое перевооружение - введены новые цехи, поточные линий, то единой тенденции показателей за весь период не будет, скорее всего нужна «периодизация» ряда, т.е. его дробление на отдельные подпериоды: до реконструкции, во время таковой (если она длительна) и после освоения новой технологии. Чем крупнее изучаемая система, чем больше факторов влияют на динамику изучаемого признака, тем реже возможны резкие, скачкообразные изменения в ряду динамики (не колебания, а именно изменения в тенденции). Большие и сложные системы обладают значительной инерцией, и для скачкообразного, резкого изменения тенденции такой системы требуются большие затраты ресурсов, которые общество выделить не в состоянии. Поэтому такое столь коренное изменение в экономике, как переход от командно-административного планового хозяйства к рыночной регулируемой экономике, в масштабе нашей страны неизбежно займет достаточно большое время, за которое сформируются новые тенденции народнохозяйственных показателей. Чтобы разглядеть эти новые тенденции, понадобится время. Напротив, в масштабе отдельных предприятий вполне возможны резкие изменения, переходы от одной тенденции к другой. Рассмотрим некоторые основные типы уравнений тренда, выражающие те или иные качественные свойства развития. А. Линейная форма тренда: у̂ = а + bt, (9.20) где у̂ — уровни, освобожденные от колебаний, выравненные по прямой; а - начальный уровень тренда в момент или период, принятый за начало отсчета времени t; b - среднегодовой абсолютный прирост (среднее изменение за единицу времени); константа тренда. Линейный тренд хорошо отражает тенденцию изменений при действии множества разнообразных факторов, изменяющихся различным образом по разным закономерностям. Равнодействующая этих факторов при взаимопогашении особенностей отдельных факторов (ускорение, замедление, нелинейность) часто выражается в • примерно постоянной абсолютной скорости изменения, т.е. в прямолинейном тренде. Таковы, например, тенденции динамики урожайности для масштаба области, республики, крупного региона, страны в целом. Б. Параболическая форма тренда: ̂у = а + bt + сt2, (9.21) где с - квадратический параметр, равный половине ускорения; константа параболического тренда. Остальные обозначения прежние. Параболическая форма тренда выражает ускоренное или замедленное изменение уровней ряда с постоянным ускорением. Такой характер развития можно ожидать при наличии важных факторов прогрессивного развития (прогрессирующее поступление нового высокопроизводительного оборудования, увеличение среднесуточного прироста живого веса поросят с возрастом и т.п.). Ускоренное возрастание может происходить в период после снятия каких-то сдерживающих развитие преград - ограничений в распределении дохода, в уровне оплаты труда, при повышении цены реализации на дефицитную продукцию. Параболическая форма тренда с отрицательным ускорением (с < 0) приводит со временем не только к приостановке роста уровня, но и к его снижению со все большей скоростью. Такой характер развития может быть свойствен производству устаревшей продукции, ликвидируемой отрасли сельского хозяйства на предприятии (ферме) и т.п. Парабола 2-го порядка (квадратическая) имеет либо максимум (если с < 0 и b > 0), либо минимум (b < 0, с > 0). Для нахождения экстремума производную параболы по времени t следует приравнять нулю и решить полученное уравнение относительно t. Например, если население города (тыс. чел.) возрастает по параболе у =1800 + 80t - 2t2, то производная по времени df/dt будет иметь вид: 80 - 4t = 0, откуда t = 20. Максимум населения будет достигнут через 20 лет после начала отсчета времени, и это максимальное население составит: ŷmax = 1800 + 80· 20 - 2·202 = 2600 тыс. человек. В. Экспоненциальная форма тренда:
где k — темп изменения в разах; константа тренда. Если k > 1, экспоненциальный тренд выражает тенденцию ускоренного и все более ускоряющегося возрастания уровней. Такой характер свойствен, например, размножению организмов при отсутствии ограничения со стороны среды: кормов, пространства, хищников, болезней. При росте по экспоненте абсолютный прирост пропорционален достигнутому уровню. Так росло население Земли в эпоху «демографического взрыва» в XX столетии; сейчас этот период заканчивается и темп роста населения стал уменьшаться. Если бы он остался на уровне 1960 - 1970 гг. т. е. около 2% прироста в год от 1985 г., когда население составило 5 млрд чел., то к 2500 г. население Земли достигло бы уровня: 5 млрд·1,02515 = 134 трлн 286 млрд человек; на 1 человека приходилось бы примерно 1 м2 всей площади суши. Ясно, что рост любого объекта по экспоненциальному закону может продолжаться только небольшой исторический период времени, ибо ресурсы для любого процесса развития всегда встретят ограничения. При k < 1 экспоненциальный тренд означает тенденцию постоянно все более замедляющегося снижения уровней динамического ряда. Такая тенденция может быть присуща динамике трудоемкости продукции, удельных затрат топлива, металла на единицу полезного эффекта (на 1 кВт ч, на 1 м2 жилой площади и т.д.) при технологическом прогрессе; экстремальных точек экспонента не имеет. Г. Логарифмическая форма тренда: у̂ = а + blogt. (9.23) Логарифмический тренд пригоден для отображения тенденции замедляющегося роста уровней при отсутствии предельного возможного значения. Замедление роста становится все меньше и меньше, и при достаточно большом t логарифмическая кривая становится малоотличимой от прямой линии. Логарифмический тренд пригоден для отображения роста спортивных достижений (чем они выше, тем труднее их улучшать), роста производительности агрегата по мере его освоения и совершенствования, повышения продуктивности скота или вообще эффективности системы при ее совершенствовании без качественных, коренных преобразований. Экстремума логарифмическая кривая не имеет. Д. Тренд в форме степенной кривой: ŷ = ath, (9.24) где b - константа тренда.
При b = 1 имеем линейный тренд, b = 2 - параболический и т.п. Степенная форма - гибкая, пригодная для отображения изменений с разной мерой пропорциональности изменений во времени. Жестким условием является обязательное прохождение через начало координат: при t = 0, у = 0. Можно усложнить форму тренда: у̃ = а + th или у̃ = а + cth, но эти уравнения нельзя логарифмировать, трудно вычислять параметры, и они крайне редко применяются. Е. Гиперболическая форма тренда:
Если b > 0, гиперболический тренд выражает тенденцию замедляющегося снижения уровня, стремящегося к пределу а. Если b < 0, тренд выражает тенденцию замедляющегося роста уровней, стремящихся в пределе к а. Следовательно, гиперболическая форма тренда подходит для отображения тенденции, процессов, ограниченных предельным значением уровня (предельным коэффициентом полезного действия двигателя, пределом 100%-ной грамотности населения и т.п.). Ж. Логистическая форма тренда:
Логистическая кривая имеет форму латинской буквы s положенной на бок, отчего еще называется эсобризной кривой. Она имеет два перегиба: от ускоряющегося роста к равномерному (вогнутость) и от равномерного роста посреди периода к замедляющемуся (выпуклость). Она подходит для отображения развития в течение длительного периода, проходящего все фазы, например процесса насыщения потребителей каким-то новым товаром, скажем, телевизорами: сначала медленный, но все ускоряющийся рост доли семей, имеющих телевизор, затем рост равномерный (примерно от 30 -40% семей до 70 - 80%). Затем рост доли семей, имеющих телевизор, замедляется по мере приближения доли к 100%. Если ymin = 0, ymax = 100% или 1, уравнение упрощается до формы
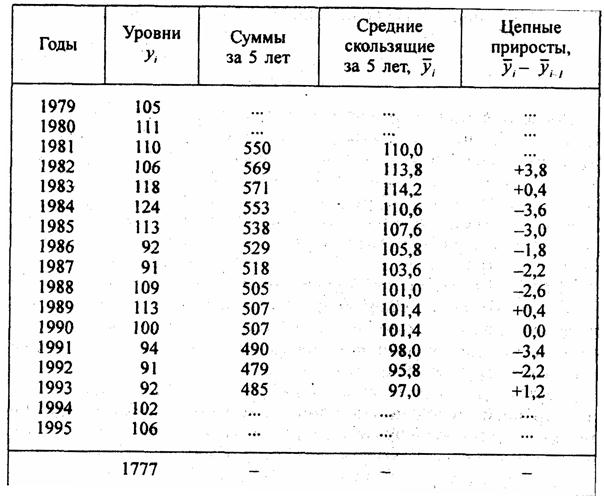
После теоретического исследования особенностей разных форм тренда необходимо обратиться к фактическому ряду динамики, тем более что далеко не всегда можно надежно установить, какой должна быть форма тренда из чисто теоретических соображений. По фактическому динамическому ряду тип тренда устанавливают на основе графического изображения, путем осреднения показателей динамики, на основе статистической проверки гипотезы о постоянстве параметра тренда. На рис. 9.1 достаточно хорошо видно, что тренд урожайности выражен прямой линией. Исходный ряд уровней короткий, поэтому на данном примере нельзя использовать другие приемы. Применим их к анализу динамики индекса цен на нетопливные товары развивающихся стран за 1979 - 1995 гг. Скользящая пятилетняя средняя, сглаживая колебания отдельных уровней, довольно отчетливо показывает тенденцию равномерного снижения уровней. Если разбить ряд на три части, то средние уровни также подтверждают этот вывод: за 1979 - 1983 гг. средний уровень равен 112,3; за 1984 - 1989 гг. - 103,0; за 1990 -1995 гг. - 97,0. Существенного различия в величине снижения среднегодовых уровней нет. Оба приема - скользящая средняя и средние уровни по частям ряда - не свободны от субъективных факторов. Можно скользящую среднюю вычислять не за 5 лет, а за 6 или 7; можно иначе разбить ряд на три части или на другое число частей. Более обоснованным приемом выявления тренда является проверка статистической гипотезы о постоянстве того или иного показателя динамики. Рассмотрим этот прием по данным табл. 9.4. Таблица 9.4 Проверка гипотезы о линейном тренде индекса цен (1990 г. = 100%) В первую очередь проверяется гипотеза о наиболее простой - линейной форме уравнения тренда, т. е. о несущественности различий цепных абсолютных изменений. Имеем 12 абсолютных изменений скользящей средней, которая хотя и сгладила сильные колебания уровней ряда, но как видим, ее абсолютные изменения далеко не одинаковы. Разбиваем эти 12 цепных приростов на два подпериода: по 6 приростов в каждом, и для каждого подпериода вычисляем среднюю Δ̅k среднее квадрагическое отклонение (СКО) как оценку генерального СКО с учетом потери одной степени свободы вариации, s
и среднюю ошибку среднего изменения тΔk по правилам, рассмотренным в главе 7:
Для проверки гипотезы о несущественности различий между средними абсолютными изменениями по подпериодам Δ̅1, Δ̅2. М. С. Каяйкина предложила проверять существенность их различий попарно по t-критерию Стьюдента. Затем методика была дополнена и усовершенствована А. И. Манеллей, предложившим проверять существенность всех различий сразу по критерию Фишера. Средняя случайная ошибка разностей двух выборочных средних оценок, как показано в гл. 7, есть корень квадратный из суммы квадратов ошибок каждой из средних, т. е.
Критерий Стьюдента для существенности различия двух среднегодовых приростов (изменений) составит:
Критическое значение критерия при уровне значимости 0,05 и при (6-1) + (6-1) = 10 степенях свободы равно 2,23 (см. Приложение 2). Фактическое значение много меньше. Следовательно вероятность того, что различие среднегодовых приростов в разные под-периоды случайно, превышает 0,05 и гипотеза о равенстве приростов не отклоняется. А значит, тенденцию динамики на реем протяжении ряда можно считать линейной. Если же гипотеза о линейности отклоняется, по скользящим средним и их цепным приростам вычисляют ускорения приростов и аналогичным методом проверяют существенность различия ускорения в подпериодах. Если несущественно различиеускорений, принимается гипотеза о том, что тренд - парабола II порядка. Если и гипотеза о постоянстве ускорений отклоняется, то по скользящей средней вычисляют цепные темпы роста и проверяют гипотезу об их постоянстве по подпериодам. Подтверждение (неотклонение) этой гипотезы означает принятие гипотезы о том, что тренд экспоненциальный. Проверка гипотез о других типах тенденций динамики, рассмотренных в п. 9.4, сложнее и здесь излагаться не будет. Итак, в нашем примере принято решение считать тренд линейным, и следует приступить к вычислению его параметров. | ||||||||||||||||||||||||||||||||




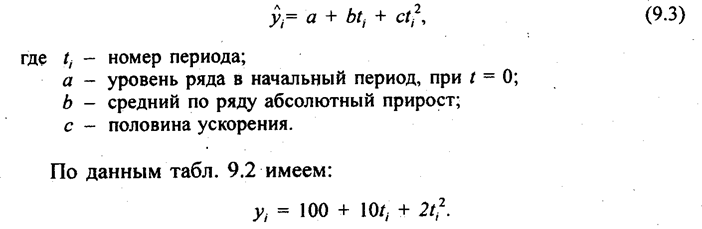
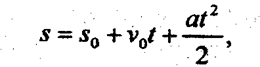


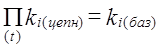
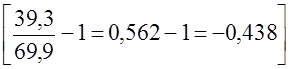


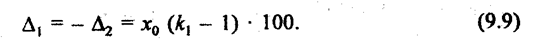


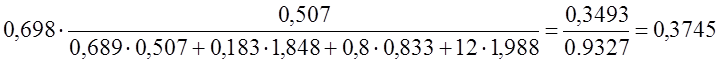
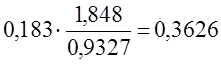 или 36,26%.
или 36,26%.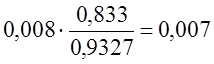 или 0,7%.
или 0,7%.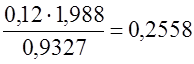 или 25,58%.
или 25,58%. 

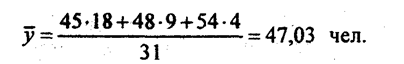
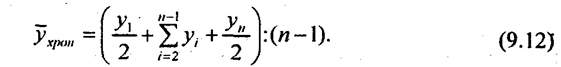

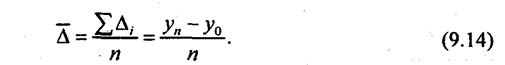
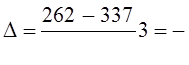 25 млн т в год. Итак, добыча угля в период 1992 - 1995 гг. в среднем за год снижалась на 25 млн т в год, или на 2,08 млн т в месяц.
25 млн т в год. Итак, добыча угля в период 1992 - 1995 гг. в среднем за год снижалась на 25 млн т в год, или на 2,08 млн т в месяц.