| ВАРИАЦИЯ – (в переводе с лат. – изменение, колеблемость, различие) это различие значений какого-либо признака у разных единиц совокупности в один и тот же период или момент времени.
Вариация порождается комплексом условий, действующих на совокупность и её единицы, и присуща всем без исключения явлениям природы и общества (за исключением законодательно закреплённых нормативных значений отдельных социальных признаков).
Измерение вариации даёт возможность оценить степень влияния на изучаемый признак других варьирующих признаков. Например, установить, какие факторы и в какой степени влияют на смертность населения, финансовое положение предприятий, урожайность пшеницы и т. п.
Для измерения вариации признака применяются различные обобщающие показатели.
1. Размах колебаний (вариации) (R) представляет собой разность между максимальным и минимальным значениями признака в изучаемой совокупности: 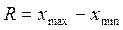 . .
2. Формулы для расчёта среднего линейного отклонения, дисперсии, среднего квадратического отклонения зависят от того, в каком виде представлены данные (сгруппированы они или нет) (таблица 6).
Таблица 6 – Показатели вариации
|
Показатель |
Для первичного ряда (по несгруппированным данным) |
Для вариационного ряда (по сгруппированным данным) |
|
Среднее линейное отклонение |
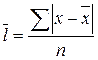
|
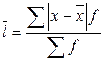
|
|
Дисперсия |
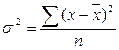
|
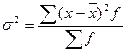
|
|
Среднее квадратическое отклонение |
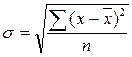
|
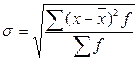
|
Качественные (альтернативные) признаки, так же как и количественные варьируют (изменяются). Вариация альтернативного признака оценивается с помощью показателя дисперсии, определяемого по формуле: 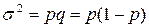 , где p – доля единиц, обладающих данным признаком; q – доля единиц, не обладающих данным признаком. , где p – доля единиц, обладающих данным признаком; q – доля единиц, не обладающих данным признаком.
При сравнении колеблемости различных признаков в одной и той же совокупности или при сравнении колеблемости одного и того же признака в нескольких совокупностях с различной средней арифметической используются относительные показатели рассеивания (вариации). К относительным показателям вариации относятся:
1) коэффициент осцилляции 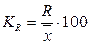 ; ;
2) относительное линейное отклонение 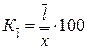 ; ;
3) коэффициент вариации 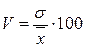 , используется для оценки типичности средней величины признака. Совокупность считается однородной, а средняя типичной для данной совокупности, если коэффициент вариации не больше 33 %. , используется для оценки типичности средней величины признака. Совокупность считается однородной, а средняя типичной для данной совокупности, если коэффициент вариации не больше 33 %.
Для оценки влияния различных факторов, определяющих колеблемость индивидуальных значений признака, используется разложение общей дисперсии на составляющие: межгрупповую дисперсию и среднюю дисперсию из внутригрупповых.
Общая дисперсия рассчитывается по всей совокупности и характеризует вариацию признака, обусловленную влиянием всех факторов, действующих в совокупности:
|
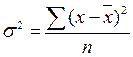 - простая дисперсия; - простая дисперсия;
|
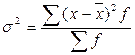 - взвешенная дисперсия - взвешенная дисперсия
|
Межгрупповая дисперсия (является мерой колеблемости частных или групповых средних вокруг общей средней) характеризует вариацию признака, обусловленную влиянием фактора, положенного в основу группировки: 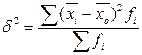 . .
Вариацию признака под влиянием прочих факторов (помимо признака-фактора, положенного в основу группировки), действующих в совокупности, характеризует средняя дисперсия из внутригрупповых (частных) дисперсий: 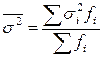 . .
Внутригрупповая (частная) дисперсия: 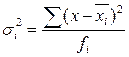 , отражает вариацию признака только за счёт условий и причин, действующих внутри группы. , отражает вариацию признака только за счёт условий и причин, действующих внутри группы.
Между названными видами дисперсий существует определённое соотношение, которое называют ЗАКОНОМ (правилом) сложения дисперсий: 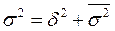 . .
Отношение межгрупповой дисперсии к общей даст коэффициент детерминации 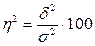 , который характеризует долю вариации результативного признака, обусловленную признаком-фактором, положенным в основу группировки, в общей вариации признака. , который характеризует долю вариации результативного признака, обусловленную признаком-фактором, положенным в основу группировки, в общей вариации признака.
Показатель, полученный как корень квадратный из коэффициента детерминации, называется эмпирическим корреляционным отношением: 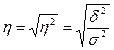 . .
Эмпирическое корреляционное соотношение характеризует тесноту связи между результативным и факторным признаками. Чем ближе эмпирическое корреляционное отношение к 1, тем теснее связь между признаками.
УПРАЖНЕНИЯ
По результатам группировки (задача 3.1) оцените тесноту связи между издержками обращения и товарооборотом магазина. Для этого вычислите общую и межгрупповую дисперсию товарооборота, коэффициент детерминации и эмпирическое корреляционное отношение с помощью вспомогательных таблиц 1 и 2. Результаты расчетов необходимых показателей представьте в таблице 3
Вспомогательная таблица 1
№ магазина |
Издержки обращения, млн. руб. |
х2 |
№ магазина |
Издержки обращения, млн. руб. |
х2 |
|
1 |
1,6 |
|
14 |
3,9 |
|
|
2 |
3,8 |
|
15 |
3,8 |
|
|
3 |
4,7 |
|
16 |
3,7 |
|
|
4 |
3,9 |
|
17 |
2,7 |
|
|
5 |
1,5 |
|
18 |
2,9 |
|
|
6 |
2,7 |
|
19 |
4 |
|
|
7 |
3,1 |
|
20 |
3,7 |
|
|
8 |
3 |
|
21 |
1,7 |
|
|
9 |
4,5 |
|
22 |
2,8 |
|
|
10 |
3,7 |
|
23 |
4 |
|
|
11 |
3,9 |
|
24 |
3,9 |
|
|
12 |
2,9 |
|
25 |
4 |
|
|
13 |
1,8 |
|
Итого: |
-- |
|
Вспомогательная таблица 2
|
Группы магазинов по объему розничного товарооборота, млн. руб. |
Число магазинов |
Издержки обращения в среднем на 1 магазин, млн. руб. |
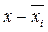
|
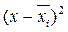
|
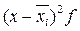
|
|
от 20 до 33 |
|
|
|
|
|
|
от 33 до 46 |
|
|
|
|
|
|
от 46 до 59 |
|
|
|
|
|
|
от 59 до 72 |
|
|
|
|
|
|
72 и более |
|
|
|
|
|
|
Итого: |
|
|
|
|
|
Таблица 3
|
Наименование показателя |
Величина |
|
Межгрупповая дисперсия |
|
|
Общая дисперсия |
|
|
Коэффициент детерминации |
|
|
Эмпирическое корреляционное отношение |
|
| 