Таблица выбора вариантов домашней контрольной работы:

Основными структурными элементами домашней контрольной работы являются:

- титульный лист;

- рецензия;

- содержание;

- основная часть;

- список использованных источников;

-  приложения (при необходимости).

ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ

Задание 1. Составить экономико-математическую модель задачи

Вар. 1. Из пункта А в пункт Б ежедневно отправляются скорые и пассажирские поезда. Наличный парк вагонов разных типов, из которых ежедневно можно комплектовать данные поезда, и число пассажиров, вмещающихся в каждом из вагонов, приведены ниже

Постройте математическую модель задачи, на основании которой можно определить количество скорых и пассажирских поездов, при которых число перевозимых пассажиров достигает максимума.

Вар. 2. Три завода выпускают комбайны, которые отправляются потребителям. Первый завод поставляет 50 комбайнов, второй – 40 комбайнов, третий – 70 комбайнов. Каждому из потребителей требуется соответственно 30, 50, 40 и 40 комбайнов. Стоимость перевозки одной единицы техники от поставщика потребителю задана матрицей стоимостей:

Постройте математическую модель задачи, обеспечивающую общую минимальную стоимость перевозки комбайнов.

Вар. 3. Фармацевтическая фирма ежедневно производит не менее 800 кг некой пищевой добавки – смеси кукурузной и соевой муки, состав которой представлен в следующей таблице.

Диетологи требуют, чтобы в пищевой добавке было не менее 30% белка и не более 5% клетчатки. Фирма хочет определить рецептуру смеси минимальной стоимости с учетом требований диетологов. Постройте математическую модель задачи.

Вар. 4. Три завода выпускают грузовые автомобили, которые отправляются четырем потребителям. Первый завод поставляет 90 платформ грузовиков, второй – 30 платформ, третий – 40 платформ. Требуется поставить платформы следующим потребителям: первому – 70 шт., второму – 30 шт., третьему – 20 шт., четвертому – 40 шт. Стоимость перевозки одной платформы от поставщика до потребителя указана в следующей таблице (д.е.):

Постройте математическую модель, на основании которой можно найти план доставки грузовых автомобилей, обеспечивающую минимальные расходы.

Вар. 5. Кондитерская фабрика для производства трех видов карамели А, В, и С использует три вида основного сырья: сахарный песок, патоку и фруктовое пюре. Нормы расхода сырья каждого вида на производство 1 т карамели данного вида, общее количество сырья каждого вида, прибыль от реализации 1 т карамели указаны в следующей таблице:

Найти план производства карамели, обеспечивающий максимальную прибыль от ее реализации.

Вар. 6. Промышленный концерн имеет два завода и пять складов в различных регионах страны. Каждый месяц первый завод производит 40 ед. продукции, а второй – 70 ед. продукции. Вся продукция, произведенная заводами, должна быть направлена на склады. Вместимость первого склада равна 20 ед. продукции, второго – 30, третьего – 15, четвертого – 27, пятого – 28 ед. продукции. Издержки транспортировки продукции от перевозки продукции до склада заданы матрицей. Распределите  план перевозок из условия минимизации ежемесячных расходов на транспортировку.

Вар. 7. В угольном бассейне добывается уголь, который хранится на трех складах в количестве 120, 60, 100 ед. соответственно. Добытый уголь доставляется четырем энергетическим установкам в количестве 70, 90, 50, и 70 ед. Стоимость доставки 1 ед. угля из  каждого  склада  соответствующим  энергетическим  установкам  задана  матрицей. Определить оптимальный план доставки угля энергетическим установкам, обеспечивающий суммарные минимальные затраты.

Вар. 8. В резерве трех железнодорожных станций А, В, С находятся соответственно 60, 80, 100 вагонов. Составить оптимальный план перегона этих вагонов к четырем пунктам погрузки хлеба, если пункту 1 необходимо 40 вагонов, пункту 2 – 60 вагонов, пункту 3 – 80 вагонов и пункту 4 – 60 вагонов. Стоимости перегонов одного вагона со станции А в указанные пункты соответственно равны 1, 2, 3, 4 д.е., со станции В – 4, 3, 2 и 1 д.е., со станции С – 1, 2, 2, 1 д.е.

Вар. 9. На складах А, В, С находится сортовое зерно 100, 150, 250 т., которое нужно доставить в четыре пункта. Пункту 1 необходимо поставить 50 т., пункту 2 – 100 т., пункту 3 – 200 т., пункту 4 – 150 т. сортового зерна. Стоимость доставки 1 т. зерна со склада А в указанные пункты соответственно равна (д. е.) 80, 30, 50, 20; со склада В – 40, 10, 60, 70; со склада С – 10, 90, 40, 30. Составьте оптимальный план перевозки зерна из условия минимума стоимости перевозки.

Вар. 10. Строительный песок добывается в трех карьерах и доставляется на четыре строительные площадки. Производительность карьеров за день составляет соответственно 45т, 35т, 40т. Потребности в песке строительных площадок составляют соответственно 30т, 40т, 50т Транспортные расходы определены матрицей. Определить план закрепления строительных площадок за карьерами, обеспечивающий минимальные расходы.

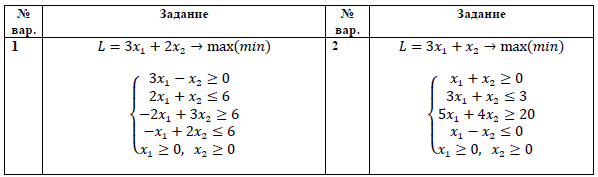
Задание 2. Решить задачи графическим методом.

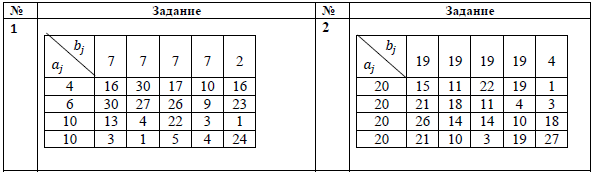
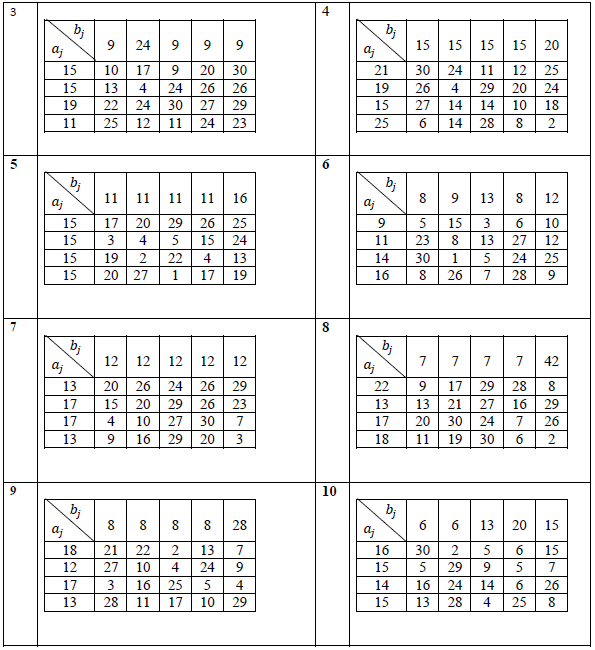
Задание 3. Условие транспортной задачи задано величинами aij – запасов поставщиков, bij – потребностей потребителей, cij – тарифов на перевозку грузов. Требуется составить план перевозок груза с минимальными транспортными издержками. Решить задачу в MS Excel.