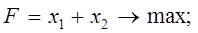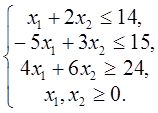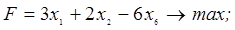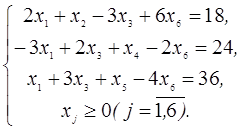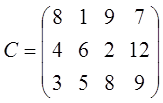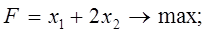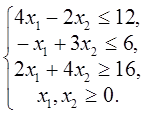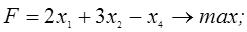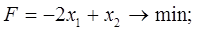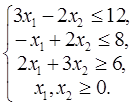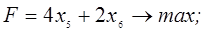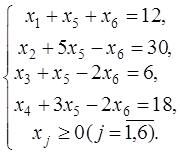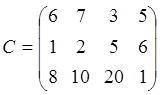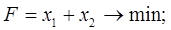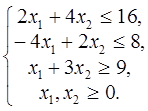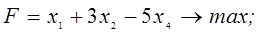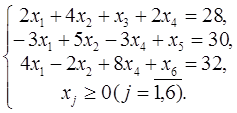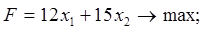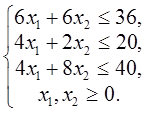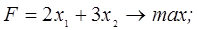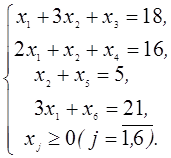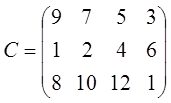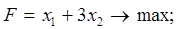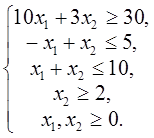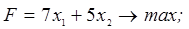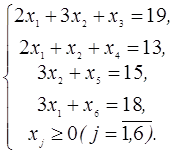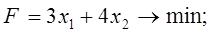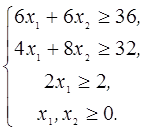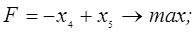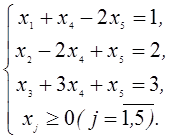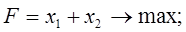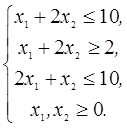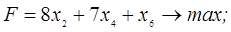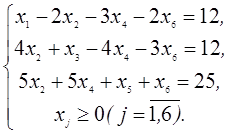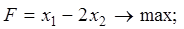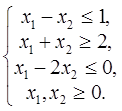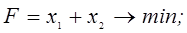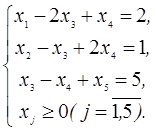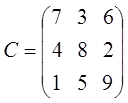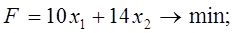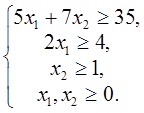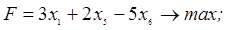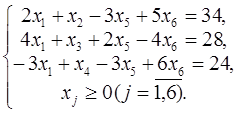Вариант № 1

1. Найти решение задачи ЛП, используя графический метод.

2. Составить математическую модель задачи.

На швейной фабрике для изготовления четырёх видов изделий может быть использована ткань трёх артикулов. Нормы расхода тканей всех артикулов на пошив одного изделия приведены в таблице. В ней же указаны имеющееся в распоряжении фабрики общее количество тканей каждого артикула и цена одного изделия данного вида. Определить сколько изделий каждого вида должна произвести фабрика, чтобы стоимость изготовленной продукции была максимальной.

3. В следующей задаче требуется: а) составить для данной задачи линейного программирования двойственную задачу; б) решить исходную задачу симплексным методом; в) по решению исходной найти решение двойственной задачи.

4. Решить транспортную задачу.

На трёх хлебокомбинатах ежедневно производится 110, 190 и 90 т муки. Эта мука потребляется четырьмя хлебозаводами, ежедневные потребности которых равны соответственно 80, 60, 170 и 80 т. Тарифы перевозок 1 т муки с хлебокомбинатов к каждому из хлебозаводов задаются матрицей

Составить такой план доставки муки, при котором общая стоимость перевозок является минимальной.

Вариант № 2

1. Найти решение задачи ЛП, используя графический метод.

2. Составить математическую модель задачи.

Предприятие выпускает четыре вида продукции и использует три типа основного оборудования: токарное, фрезерное и шлифовальное. Затраты времени на изготовление единицы продукции для каждого из типов оборудования приведены в таблице. В ней же указаны общий фонд рабочего времени каждого из типов оборудования, а также прибыль от реализации одного изделия данного вида. Определить такой объём выпуска каждого  из изделий, при котором общая прибыль от их реализации является максимальной.

3. В следующей задаче требуется: а) составить для данной задачи линейного программирования двойственную задачу; б) решить исходную задачу симплексным методом; в) по решению исходной найти решение двойственной задачи.

8. Решить транспортную задачу.

Вариант № 3

1. Найти решение задачи ЛП, используя графический метод.

2. Составить математическую модель задачи.

Для поддержания нормальной жизнедеятельности человеку ежедневно необходимо потреблять не менее 118 г белков, 50 г жиров, 500 г углеводов, 8 г минеральных солей. Количество питательных веществ, содержащихся в 1 кг каждого вида потребляемых продуктов, а также цена 1 кг каждого из этих продуктов приведены в следующей таблице:

Составить дневной рацион, содержащий не менее минимальной суточной нормы потребности человека в необходимых питательных веществах при минимальной общей стоимости потребляемых продуктов.

3. В следующей задаче требуется: а) составить для данной задачи линейного программирования двойственную задачу; б) решить исходную задачу симплексным методом; в) по решению исходной найти решение двойственной задачи.

4. Решить транспортную задачу.

Для строительства четырёх объектов используется кирпич, изготовляемый на трёх заводах. Ежедневно каждый из заводов может изготовлять 100, 150, и 50 усл. ед. Ежедневные потребности в кирпиче на каждом из строящихся объектов соответственно равны 75, 80, 60 и 85 усл. ед. Известны также тарифы перевозок 1 усл. ед. кирпича с каждого завода к каждому из строящихся объектов:

Составить такой план перевозок кирпича, при котором общая стоимость перевозок является минимальной.

Вариант № 4

1. Найти решение задачи ЛП, используя графический метод.

2. Составить математическую модель задачи.

Цех мебельного комбината выпускает трельяжи, трюмо и тумбочки под телевизоры. Норма расхода материала в расчете на одно изделие, плановая себестоимость, оптовая цена предпри­ятия, плановый (месячный) ассортимент и трудоемкость единицы продукции приведены в таблице. Запас древесностружечных плит, досок еловых и березовых 90, 30 и 14 м³ соответственно. Плановый фонд рабочего времени 16800 человеко-часов.

Исходя из необходимости выполнения плана по ассортименту и возможности его перевыполнения по отдельным (или даже по всем) показателям построить модели, на основе которых можно сформулировать задачу максимизации объема реализации (за плановый период).

3. В следующей задаче требуется: а) составить для данной задачи линейного программирования двойственную задачу; б) решить исходную задачу симплексным методом; в) по решению исходной найти решение двойственной задачи.

4. Решить транспортную задачу.

Вариант № 5

1. Найти решение задачи ЛП, используя графический метод.

2. Составить математическую модель задачи.

Сформулировать задачу оптимального раскроя по следующим данным:

3. В следующей задаче требуется: а) составить для данной задачи линейного программирования двойственную задачу; б) решить исходную задачу симплексным методом; в) по решению исходной найти решение двойственной задачи.

4. Решить транспортную задачу.

В трёх хранилищах горючего ежедневно хранится 175, 125 и 140 т бензина. Этот бензин ежедневно получают четыре заправочные станции в количествах равных соответственно 180, 110, 80 и 70 т. Стоимости перевозок 1 т бензина с хранилищ к заправочным станциям задаются матрицей

Составить такой план перевозок бензина, при котором общая стоимость перевозок является минимальной.

Вариант № 6

1. Найти решение задачи ЛП, используя графический метод.

2. Составить математическую модель задачи.

На приобретение оборудования для нового производственного участка выделено 300 тыс. руб. Его предполагается разместить на площади 45 кв.м. Участок может быть оснащен оборудованием трех видов - машинами стоимостью 6 тыс. руб. (здесь и далее все показатели приводятся на единицу оборудования), размещающимися на площади 9 кв. м, производительность 8 тыс. единиц продукции за смену; машинами стоимостью 3 тыс. руб., занимающими площадь 4 кв. м. и производительностью 4 тыс. единиц продукции за смену; машинами стоимостью 2 тыс. руб., занимающими площадь 3 кв.м., производительностью 3 тыс. единиц продукции.

Построить модель, на основе которой можно сформулировать экстремальную задачу определения плана приобретения оборудования, обеспечивающего наибольшую производительность всего участка.

3. В следующей задаче требуется: а) составить для данной задачи линейного программирования двойственную задачу; б) решить исходную задачу симплексным методом; в) по решению исходной найти решение двойственной задачи.

9. Решить транспортную задачу.

Вариант № 7

1. Найти решение задачи ЛП, используя графический метод.

2. Составить математическую модель задачи.

Дана следующая информация:

Составить план производства продукции, минимизирующий суммарную себестоимость выпуска и обеспечивающий выполнение по объёму реализации продукции в количестве 180 тыс. руб.

3. В следующей задаче требуется: а) составить для данной задачи линейного программирования двойственную задачу; б) решить исходную задачу симплексным методом; в) по решению исходной найти решение двойственной задачи.

4. Решить транспортную задачу.

Три хозяйства выделяют соответственно 11, 11 и 8 т молока для ежедневного снабжения четырёх пунктов, потребности которых составляют соответственно 5, 9, 9 и 7 т молока. Стоимости перевозок от каждого хозяйства к каждому пункту снабжения составляют:

Требуется организовать снабжение таким образом, чтобы добиться минимальных транспортных расходов.

Вариант № 8

1. Найти решение задачи ЛП, используя графический метод.

2. Составить математическую модель задачи.

В плановом году строительные организации города переходят к сооружению домов типов Д-1, Д-2, Д-3 и Д-4. Данные о количестве квартир разного типа в каждом из указанных типов домов, их плановая себестоимость приведены в таблице. Годовой план ввода жилой площади составляет соответственно 800, 1000, 900, 2000 и 7000 квартир указанных типов.

Исходя из необходимости выполнения плана ввода квартир (возможно его перевыполнения по всем показателям) и обеспеченности строительными материалами и трудовыми ресурсами, построить мо­дель и сформулировать на ее основе экстремальную задачу нахождения плана строительс­тва на финансовый год, при котором себестоимость всех вводимых домов будет минимальной.

3. В следующей задаче требуется: а) составить для данной задачи линейного программирования двойственную задачу; б) решить исходную задачу симплексным методом; в) по решению исходной найти решение двойственной задачи.

4. Решить транспортную задачу.

Вариант № 9

1. Найти решение задачи ЛП, используя графический метод.

2. Составить математическую модель задачи.

Цех выпускает три вида изделий. Суточный плановый выпуск: 90 ед. изделия I, 70 ед. изделия II и 60 ед. изделия III. Суточные ресурсы: 780 ед. производственного оборудования, 850 ед. сырья и 790 ед. электроэнергии. Их расход на одно изделие указан в таблице. Стоимость изделия I – 8 ден. ед., изделия II – 7 ден. ед., изделия III – 6 ден. ед. Сколько надо производить изделий каждого вида, чтобы стоимость продукции, выпущенной сверх плана, была максимальной?

3. В следующей задаче требуется: а) составить для данной задачи линейного программирования двойственную задачу; б) решить исходную задачу симплексным методом; в) по решению исходной найти решение двойственной задачи.

4. Решить транспортную задачу.

Имеется три склада и три магазина. На складах имеется груз в количестве 74, 40 и 36 ед. соответственно. Потребность магазинов составляет соответственно 20, 45 и 85 ед. Стоимости перевозок от каждого склада к каждому магазину составляют:

Найти такой план перевозок, чтобы общая стоимость всех перевозок была минимальной.

Вариант № 10

1. Найти решение задачи ЛП, используя графический метод.

2. Составить математическую модель задачи.

Имеются два проекта на строительство жилых домов. Расход стройматериалов, их запас и полезная площадь дома каждого проекта приведены в таблице. Определить, сколько домов первого и второго проекта следует построить, чтобы полезная площадь была наибольшей.

3. В следующей задаче требуется: а) составить для данной задачи линейного программирования двойственную задачу; б) решить исходную задачу симплексным методом; в) по решению исходной найти решение двойственной задачи.

4. Решить транспортную задачу.