Тема 1. Потребление и спрос

Задача 1.

 На основе данных таблицы выполните следующие задания:

а) составьте кривые спроса потребителей А, B, C на графиках;

б) начертите кривую рыночного спроса;

в) составьте уравнение кривой рыночного спроса;

г) если спрос на товар со стороны потребителя А удвоится, а со стороны С – сократится наполовину, то как изменится кривая рыночного спроса

Задача 2.

Функции спроса и предложения представлены уравнениями:

Q_d = 7 – Р,  Q_s = – 5  + 2Р.

а) определите равновесные цену и количество;      

б) составьте  график кривых спроса и предложения;

в) покажите новое расположение кривых спроса и предложения, если покупатели и продавцы не реагируют на изменение цены от 3,5 до 2,5 руб.

г) каким будет расположение кривых спроса и предложения, если объем предложения совершенно  не изменяется и составляет 7 единиц.

Задача 3.

Степанов С. С. свой доход в размере 100 руб. тратит на приобретение молока и хлеба. Стоимость продуктов питания:

Молока - Рx = 10 руб. за 1 л,

Хлеба - Рy = 5 руб. за 1 кг.

Предпочтения потребителя описываются следующей функцией полезности: U(x; y) = x^1/4 y^1/2

1. Установите, насколько изменится оптимальный набор потребителя, если его доход возрастет в два раза.

2. Насколько изменится оптимальный набор потребителя, если его предпочтения станут описываться функцией полезности вида:

U(x; y) = x^1/3 y^3/4

Тема 2. Теория производства

Задача 1.

 Выпуск продукции за день для производственной функции Q = 2(K,L) показан в следующей таблице:

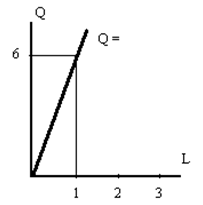
а) определите Q, если пр. функция = 2(K₄,L₄);

б) составьте по данным таблицы пр. функцию, если выпускается 24 изделия;

в) выразите на графике пр. функцию Q = f(K,L) = 2L;

г) исходя из условия задачи, выразите данные графика через пр. функцию;

д) изобразите на графике пр. функцию Q = 2(ÖK,ÖL), когда К остаётся постоянным и равным 4.

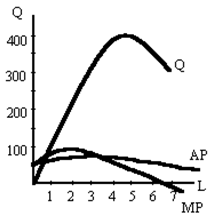
Задача 2.

Изобразите на графике пр.функцию для f(K,L) = ÖKÖL, когда К остается постоянным при К₀ = 4.

Задача 3.

Технологический процесс выпуска продукции на фирме выражает производственная функция:   Q = 8L² + 50KL – 2L³, где L – число нанятых рабочих, К- используемые единицы капитала. Пусть капитал фиксирован и К = 1, а максимальное количество рабочих будет 6 человек.

Составьте таблицу, в которой покажите общий объем продукции фирмы, среднюю и предельную производительность труда.

Задача 4.

Изобразите на графике кривые общего объема продукции в краткосрочном периоде на основании следующих производственных функций, если капитал фиксирован на уровне К₀ = 4.

а) Q = Ф(K,L) = 2K + 3L;

б) Q = Ф(K,L) = 2ÖL;

в) Q = Ф(K,L) = K²L²;

г) подчиняются ли указанные функции закону убывающей отдачи?

Задача 5.

Технологический процесс выпуска продукции характеризует пр. функция с результатами, изображенными на графике:

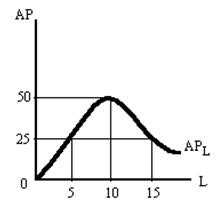
а) когда начинается убывающая отдача труда?

б) если бы фирма хотела сохранить средний продукт (АР) максимальным, то сколько рабочих она стала бы нанимать?

в) представьте, что сейчас у фирмы АР_L = MP_L. Если бы вы были одним из нескольких новых рабочих, которых фирма собирается принять на работу, то вы предпочли бы:

1) чтобы вам платили стоимость вашего среднего продукта;

2) или стоимость вашего предельного продукта?

г) если владелец фирмы сказал рабочему, который ищет работу, что он не нанял бы еще одного рабочего, даже если тот согласится работать бесплатно, то мы вправе предположить, что:

1) средний продукт рабочих = 0;

2) средний продукт рабочих возрастает;

3) средний продукт рабочих отрицательный;

4) средний продукт рабочих  понижается.

д) Один шутник заметил, что когда известный правительственный деятель переехал из Нью-Йорка в Калифорнию, то средний коэффициент умственного развития в обоих штатах повысился. Почему?

Задача 6.

На основе диаграммы о средней производительности труда (АР) на фирме ответьте на следующие вопросы:

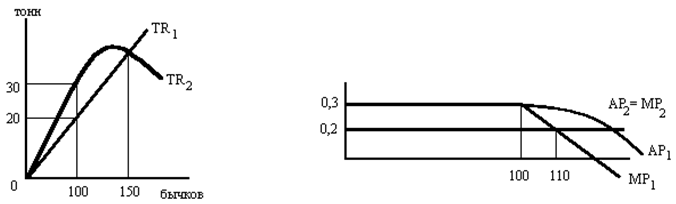
а) если АР_L имеет максимум в точке L = 10, то можно ли считать, что общий продукт труда Q также имеет максимум в точке L = 10?

б) если МР 15-й единицы труда имеет отрицательное значение, значит ли это, что АР_L в этой точке имеет отрицательную величину?

в) если АР_L = 40 при L = 8, а МР 9-ой единицы труда = 60, то каков общий продукт труда при L = 9?

г) чему равен общий продукт фирмы, если АР_L = 25?

д) при какой численности рабочих АР_L = МР_L?

Задача 7.

ООО "Прогресс" имеет 200 молодых бычков, которых нужно распределить по двум пастбищам. Если на 1-е небольшое пастбище направить любое количество бычков, но не более 100, то каждый бычок даст привес 300 кг в год, а если бычков будет свыше 100, то привес каждого будет быстро сокращаться.

Качество травы на 2-м пастбище ниже, но пасти здесь можно неограниченное количество бычков и годовой привес каждого составит 200 кг. 

Соответствующие кривые общей продукции с двух пастбищ показаны на графике. Имея эти данные, нужно наилучшим способом распределить стадо бычков по двум пастбищам.

а) Начертите график кривых средней и предельной производительности АР и МР для обоих пастбищ, если при 110 бычках на первом пастбища МР₁=МР₂;

б) сколько нужно бычков направить на 1-е и 2-е пастбища?;

в) определите общий объем привеса на двух пастбищах, если на 1-е направить 90 бычков, а на 2-е – 110;

г) если бы MР₁ было меньше МР₂, то каким образом нужно распределить стадо и каков будет общий привес;

д) во сколько тонн убытка обойдется решение проблемы распределения ресурсов не по правилу МР₁=МР₂, а по обычно применяемому правилу равенства средних продуктов или средней производительности (АР₁=АР₂).

Задача 8.

При данном объеме производства менеджер фирмы определил, что МР_L = 5 единицам продукции в неделю, а МР_К = 10.

а) определите МRTS капитала трудом;

б) на сколько единиц нужно увеличить труд, если капитал уменьшим на 2 единицы из-за роста цен?

в) по мере замещения капитала трудом MRTS_LK будет снижаться и возрастать.

Задача 9.

У фирмы, имеющей заданный размер капитала, вводится рабочая сила. МР_L = 3. Если норма замещения капитала трудом равна 9, то каким будет МР_К?

Задача 10.

Производственная функция Q = 2KL имеет следующую таблицу результатов:

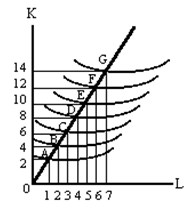
1. Покажите на графике карту изоквант, которая имеет 4 различных объёма производства. Поставьте числовые значения координат и обозначьте величину объёма производства для всех изоквант.

2. Имеет ли производственная функция сокращающийся доход?

3. Имеются ли снижающийся, неизменный возрастающий эффекты масштаба?

Задача 11.

Пусть капитал зафиксирован и К₀ = 4 в произв. функции Q = Ф(K,L) = KL.

а) покажите на графике кривые общего объема продукции, МР и АР при изменении рабочей силы от 1 до 4 человек;

б) если фирма расширилась, удвоив затраты К и L, но действует постоянный эффект масштаба производства, то покажите, что AP_L и AP_K остаются постоянными, независимо от того, в каких количествах труд и капитал используются при постоянной пропорции между К и L.

Задача  12.

На графике представлена карта изоквант.

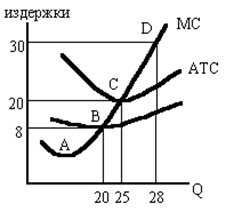
Определите:

а) На сколько возрастают факторы производства и объём продукции в точках B, C, …, G?

б) в районе каких точек пр. функция Q = Ф(K,L) выражает:

– возрастающий эффект масштаба;

– постоянный эффект масштаба;

– снижающийся эффект масштаба?

Задача  13.

Один час инженерного труда стоит 50 руб., а час труда маляра – 20 руб. Инженер решил сам провести ремонт своей квартиры и умеет выполнять все необходимые работы не хуже маляра. На ремонт квартиры инженеру требуется 30 часов (помогает вся семья), а маляру – 40 часов. Стоимость материалов для ремонта составляет 6000 руб.

Определите величину экономических (альтернативных) издержек:

1500, 600, 7500, 800, 2000, 8000 руб.?

Задача 14.

Используя диаграмму, изображенную ниже, ответьте на вопросы:

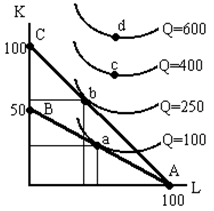
а) В какой точке появляется сокращающийся доход (убывающая отдача)?

б) Какие кривые и куда сдвинутся, если;

1. повысился налог, на имущество фирмы;

2. повысились тарифы на э/энергию;

3. повысилась номинальная зарплата рабочих.

в) Чему равны TVC производства 20 штук изделий ?

г) если при выпуске 10 изделий AFC составят 12,5 руб., то каковы AVC при выпуске 25 изделий?

д) постройте на диаграмме (для любого объема продукции) прямоугольник, площадь которого соответствует величине ТFС;

е) средние переменные издержки (AVC) начинают повышаться раньше, чем АТС потому, что:

1. на AVC не воздействуют понижающиеся AFC;

2. на AVC не воздействуют предельные издержки (МС);

3. на АТС не воздействуют возрастающие предельные издержки;

4. на АТС не воздействует сокращающийся доход.

Задача 15.

Пусть функция производства выражена уравнением Q = 3 KL. Цена капитала – 2 долл. за машино-час, цена труда – 24 долл. за чел/час. Капитал = 4 и фиксирован а краткосрочном периоде. 

а) выразите на графике производственную функцию;

б) из функции производства выведите функцию общих затрат (ТС);

в) составьте график кривых TFC, TVC, ТС;

г) составьте функции АFС, АVС, АТС и МС и покажите на графике кривые этих издержек.

Задача 16.

Предположим, что зарплата составляет 10 руб. в час, а цена капитала (например, арендная плата за работу машин) составляет 20 руб. в час. Фирма может выделить на покупку ресурсов 8000 руб.

а) покажите на графике линию изокосты, располагая объём ч/часов на горизонтальной оси, а машино-часы – на вертикальной оси;

б) определите угол наклона изокосты различными способами;

в) составьте уравнение изокосты;

г) покажите на графике новую линию изокосты, если при прочих равных условиях фирма увеличит затраты на ресурсы до 10000 руб.;

д) покажите линию изокосты при ТС = 8000, если зарплата повысится в 2 раза;

е) покажите линию изокосты при ТС = 8000, если цена капитала сократится в 2 раза.

Задача 17.

Если фирма сводит к минимуму издержки для заданного объёма продукции и МР_L = 5, МР_К = 15 и цена единицы капитала = 300 руб., то цена рабочей силы должна быть:

а) 900, б) 400, в) 100 руб.?

Задача 18.

На графике представлена карта изоквант с первоначальной изокостой АВ и новой изокостой АС. Фирма предполагает максимизировать прибыль и направляет 500 долл. на покупку ресурсов.

Ответьте на вопросы:

а) Какова первоначальная цена капитала?

б) Какова первоначальная цена труда?

в) Какова новая цена капитала?

г) В какой точке фирма первоначально находится в состоянии равновесия?

д) Какова новая точка равновесия?

е) Напишите уравнения для изокосты АВ и для изокосты АС.

ж) Каковы относительные значения МР_К и МР_L в точке “b”? Почему?

з) Каковы относительные значения МР_К и МР_L в точке “а”? Почему?

и) Может ли фирма находиться в точке “с”? В каком случае точка “с” окажется достижимой?

к) Определите наклон линий АВ и АС.

л) Как можно выразить наклон изокванты Q = 100 в точке “а”?

Тема 3. Рыночные структуры

Задача  1.

Спрос на продукцию совершенно конкурентной отрасли представлен функцией Q_D = 55 – P, а предложение Q_S = 2 Р – 5. Если у фирмы функция совокупных издержек ТС = 20 – 4 q – 0,5 q², то при каких цене и объёме фирма максимизирует прибыль?

Задача  2.

Допустим в совершенно конкурентной отрасли 20 однотипных фирм с постоянными в долгосрочном периоде издержками. Предельные издержки для краткосрочного и долгосрочного периодов одинаковы у всех фирм и задаются уравнением МС = q² – 12 q + 36? Где q – выпуск фирмы. Если рыночный спрос для обеих периодов задан уравнением Р = 189 – Q, а средние издержки производства фирм минимизируются в краткосрочном периоде – при выпуске q = 8 и долгосрочном – выпуске q = 9 единиц.

Находится ли данная отрасль в состоянии долгосрочного равновесия? К каким результатам приведет проникновение на рынок фирм, которые предложат продукции по 5 тыс. руб. за единицу?

Задача  3.

Кривая спроса на товар монополиста выражается уравнением Р = 100 – Q. Предельные издержки будут неизменными и равны 20 руб. ТFС = 500.

а) Составьте график положения фирмы на рынке;

б) Какой будет экономическая прибыль фирмы?

в) Если фирма максимизирует прибыль, то какие чистые убытки обществу  приносит стратегия фирмы? 

г) Если налог на прибыль составляет 25%, то какими будут: цена ______, объем выпуска ______, чистая прибыль ______.

д) Если бы фирма смогла провести совершенную ценовую дискриминацию, то какими были бы:

– выпуск продукции _____

– прибыль фирмы ______

Задача 4.

В двух таблицах показаны зависимость общих издержек предприятия от выпуска продукции и зависимость объема спроса от цены товара:

Предположим, что данная фирма является монополией.

Рассматривая цену спроса как функцию от объёма:

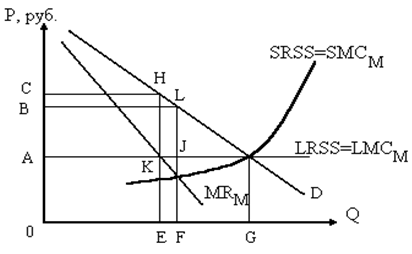
а) изобразите на графике кривые спроса, предельного дохода, предельных издержек и средних общих издержек;

б) определите:

– объём выпуска ______

– цену фирмы ______

– сумму прибыли ______

в) Каким образом ответы на вопросы в пункте б) можно получить с помощью таблицы, составленной по исходным данным?

Задача 5.

Кривая спроса монополии может быть выражена как Р = 3000 – 100 Q. Монополия имеет общие постоянные издержки ТFС = 1000 руб. и предельные издержки МС = 200 руб.

а) каким будет уравнение общих издержек?

б) предельных издержек?

в) совокупного дохода (выручки от реализации)?

г) предельного дохода?

д) каким будет выпуск продукции при максимизации прибыли?

Задача 6.

Единственная фирма установила монопольную власть над всей ранее конкурентной отраслью. В результате кривая долгосрочного предложения отрасли (LRSS) становится кривой долгосрочных предельных издержек монополии (LMC_M), а кривая краткосрочного предложения отрасли (SRSS) –кривой краткосрочных МС монополии (SMC_М). Эта ситуация изображена на рисунке:

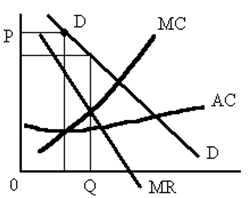
а) Какие параметры цены и отраслевого выпуска были присущи для условий совершенной конкуренции?

б) Какую цену и величину выпуска выберет монополия на краткосрочный период?

в) При каких параметрах цены и объема выпуска монополия максимизирует прибыль в долгосрочном периоде?

г) Каков размер этой долгосрочной прибыли?

Задача 7.

На рисунке представлена фирма, действующая в условиях монополистической конкуренции:

а) При каком объеме производства фирма максимизирует свою прибыль?

б) По какой цене фирма будет продавать данный объем продукции?

в) Будет ли фирма получать в этой ситуации экономическую прибыль? Если да, то какова величина прибыли?

г) Как может измениться ситуация на долгосрочном временном интервале? Опишите.

Задача 8.

На рисунке представлена фирма, действующая в условиях монополистической конкуренции:

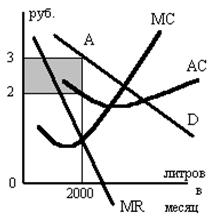
а) Фирма допустит ошибку, если установит цену, равную 0Р, потому что:

1. При этой цене MR выше МС;

2. Эта цена выше уровня цены, при которой фирма может получить максимум прибыли;

3. Объем выпуска, соответствующий этой цене, меньше того объема, при котором прибыль максимальная;

4. Все предыдущие ответы верны;

5. Верны только ответы 1 и 2.

б) Если фирма выберет объем выпуска 0Q, то:

1. На рынке возникнут новые производители товаров;

2. Фирма будет получать экономическую прибыль;

3. Фирма установит цену 0Р;

4. Все предыдущие ответы верны;

5. Верны только ответы 1 и 2.

Задача 9.

Фирма выпускает прохладительный напиток, отличающийся от конкурентных налитков вкусом и большей мерой натуральных добавок. На графике показано краткосрочное равновесие фирмы, максимизирующей прибыль:

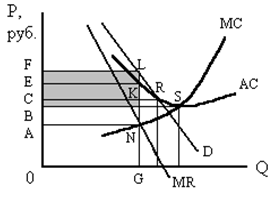
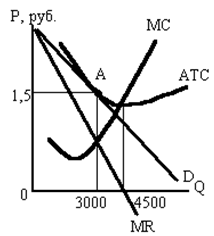
а) чему равна прибыль с единицы товара ______ и от общего объема продаж _____;

б) могут ли фирмы отрасли извлекать большую прибыль, чем нормальная прибыль?

в) сможет ли данная фирма поднять цену своего напитка без падения объема продаж до нуля и почему?

г) как может измениться ситуация для данной фирмы в долгосрочном периоде и почему?

Задача 10.

Фирма, рассматриваемая в задаче №13, оказалась в условиях, когда при цене товара в 1,5 руб. экономическая прибыль равна 0, хотя МС при выпуске 3000 литров напитка значительно ниже 1,5 pyб. AТС минимальны при выпуске 4500 литров в месяц.

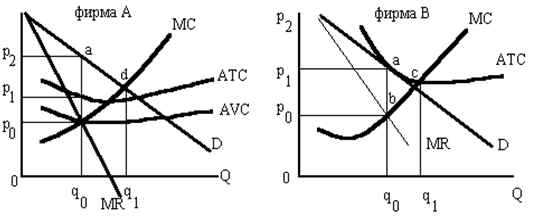
В соответствии с графиком объясните:

а) В чем причина несовпадения между АТС и МС?

б) Чем является разность между количеством товара, равного 4500 литров, и количеством 3000 литров, выпускаемом в долгосрочном периоде?

в) Чему равна избыточная мощность, которая в долгосрочном плане равновесия не используется фирмой?

г) Что означает избыточная мощность при монополистической конкуренции?

д) Почему экономия ресурсов, которая должна обеспечивать снижение АТС, несовместима с дифференциацией продукта?

Задача 11.

Два графика демонстрируют положение двух фирм на рынке монополистической конкуренции. Используя данную информацию, определите, верны (В) или неверны (Н) следующие утверждения:

а) Фирма В оперирует на долгосрочном временном интервале;

б) Фирма А максимизирует общий доход при объеме выпуска продукции q₁;

в) Фирма А оперирует на долгосрочном временном интервале;

г) Фирма А несет экономические убытки;

д) Точка “d” лежит на эластичном участке кривой спроса фирмы А;

е) Точка “a” лежит на эластичном участке кривой спроса фирмы В;

ж) Фирма В максимизирует чистый выигрыш общества при объеме q₁;

з) Фирма А максимизирует прибыль при объеме q₁;

и) Обе фирмы оперируют на избыточных производственных мощностях;

к) Фирма А будет получать экономическую прибыль независимо от того, на каком временном интервале она функционирует.