Контрольная работа № 1

Таблица 2 – Таблица выбора вариантов индивидуального задания

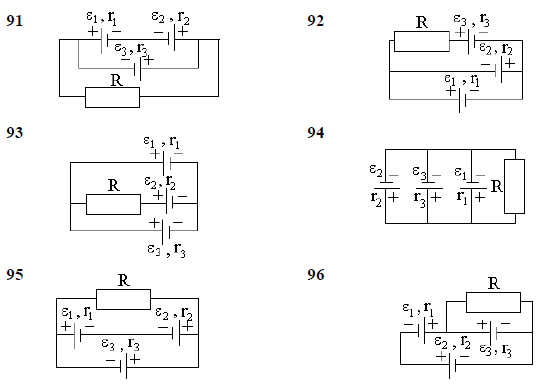
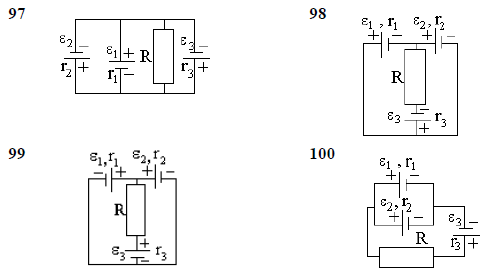
1 При прямолинейном движении зависимость координаты тела от времени описывается уравнением  х=A+Bt+Ct²+Dt³, где В=2 м/с, С=0,14 м/с², D=0,1 м/с³. Через сколько времени после начала движения ускорение тела будет равно а) 1 м/с²; б) 6 м/с²? Чему равна средняя скорость тела за промежуток времени, в течение которого ускорение возросло от 1 м/с² до 6 м/с²?

2 Зависимость координаты тела от времени задана уравнением x=At+Bt²+Ct³, где A=12 м/c, B=-3 м/с², C=-4 м/c³. Найти в явном виде зависимость скорости и ускорения от времени; расстояние, пройденное телом, мгновенные скорость и ускорение тела через 2 секунды после начала движения; среднюю скорость за промежуток времени от t₁=2 c до t₂=5 с.

3 Две материальные точки движутся согласно уравнениям: x₁=A₁t+B₁t²+C₁t³;  x₂=A₂t+B₂t²+C₂t³,  где  А₁=4 м/с, В₁=8 м/с², С₁=-16 м/с³; А₂=2 м/с, В₂=-4 м/с², С₂=1 м/с³. В какой момент времени ускорения этих точек будут одинаковы? Найти скорости точек в этот момент. Найти среднюю скорость второй материальной точки за промежуток времени с момента начала движения до момента равенства их ускорений.

4 Движения двух материальных точек выражаются уравнениями: x₁=A₁t+B₁t²+C₁t³;   x₂=A₂t+B₂t²+C₂t³,   где А₁=20 м/с,  В₁=2 м/с²,  С₁= -4 м/с³; А₂=2 м/с, В₂=2 м/с², С₂=0,5 м/с³. В какой момент времени скорости этих точек будут одинаковыми? Определить скорости и ускорения точек в этот момент. Найти среднюю скорость первой точки за промежуток времени с момента начала движения до момента равенства их скоростей.

5 Движение материальной точки задано уравнением x=Аt+Вt², где А=4м/с, В=-0,05 м/с². Определить момент времени, в который скорость точки равна нулю. Найти путь, пройденный точкой, координату и ускорение точки в этот момент. Найти среднюю скорость точки за промежуток времени с момента начала движения до момента равенства ее скорости нулю.

6 Движения двух материальных точек выражаются уравнениями: x₁=A₁+B₁t²+C₁t³;  x₂=A₂t+B₂t²+C₂t³,  где  А₁=-12 м,  В₁=-2 м/с²,  С₁= 8 м/с³; А₂=-4 м/с, В₂=-3 м/с², С₂=8 м/с³. В какой момент времени координаты этих точек будут одинаковыми? Определить скорости и ускорения точек в этот момент. Найти среднюю скорость первой точки за промежуток времени с момента начала движения до момента равенства их координат.

7 Уравнение движения тела имеет вид х=15t 0,4t². Определить промежуток времени после начала движения, в течение которого точка вернется в исходное положение. Найти путь, пройденный точкой и ее среднюю скорость за этот промежуток времени.

8 Уравнение движения материальной точки по прямой имеет вид х=А+Вt+Сt², где А=4 м, В=2 м/с, С=-0,5 м/с². Для момента времени t₁=2 с определить координату точки и мгновенное ускорение. Найти путь, пройденный точкой, и среднюю скорость за промежуток времени от t₁=2 с до t₂=6 с.

9 Зависимость координаты тела от времени дается уравнением S=A-Bt+Ct²+Dt³, где А=6 м, В=3м/с, С=-2 м/с², D=0,2 м/с³. Считая движение прямолинейным, определить для тела в интервале времени от t₁=1 c до t₂=4 с 1) среднюю скорость; 2) путь, пройденный телом; 3) в какой момент времени после начала движения точка вернется в исходное положение?

10 Две материальные точки движутся согласно уравнениям: x₁=A₁t +C₁t³; x₂=A₂t+B₂t²+C₂t³, где А₁=14 м/с, С₁=-6 м/с³; А₂=2 м/с, В₂=4 м/с², С₂=-5 м/с³. В какой момент времени t₁ ускорение первой точки будет вдвое больше ускорения второй? Найти скорости точек в этот момент. Найти среднюю скорость первой точки за промежуток времени с момента начала движения до момента времени t₁.

11 Тело некоторой массы скользит вниз по наклонной плоскости с постоянным ускорением, равным 0,05g. Найти угол наклона этой плоскости, если коэффициент трения равен 0,02.

12 За какое время тело спустится с вершины наклонной плоскости высотой 3 м и углом у основания 60⁰ , если максимальный угол у основания наклонной плоскости, при котором тело находится на ней в покое, равен 30⁰ ?

13 Тело массой m скользит по наклонной плоскости, образующей с горизонтом угол 45⁰ . Зависимость пройденного телом пути от времени дается уравнением s=Ct², где С=1,73 м/с 2 . Найти коэффициент трения тела о плоскость.

14 На автомобиль массой 1т во время движения действует сила трения, равная 0,1 действующей на него силы тяжести. Найти силу тяги, развиваемую мотором автомобиля, если автомобиль движется с ускорением 1 м/с² в гору с уклоном 1 м на каждые 25 м пути.

15 По наклонной плоскости с углом a наклона к горизонту, равным 30⁰ , скользит тело. Определить скорость тела в конце второй секунды от начала скольжения, если коэффициент трения m =0,15.

16 С каким ускорением будет скользить тело по наклонной плоскости, образующей с горизонтом угол a =24 ⁰ , если коэффициент трения равен 0,03? Какое время потребуется для прохождения при этих условиях пути 100 м? Какую скорость тело будет иметь в конце пути?

17 С вершины клина, длина которого ℓ =2 м и высота h=1 м, начинает скользить небольшое тело. Коэффициент трения между телом и клином m =0,15. Определить: 1) ускорение, с которым движется тело; 2) время прохождения тела вдоль клина; 3) скорость тела у основания клина.

18 На автомобиль массой 2т во время движения действует сила трения, равная 0,1 действующей на него силы тяжести. Найти силу тяги, развиваемую мотором автомобиля, если автомобиль движется с постоянной скоростью в гору с уклоном 1 м на каждые 25 м пути.

19 Тело некоторой массы равномерно скользит вниз по наклонной плоскости. Найти угол наклона этой плоскости, если коэффициент трения равен 0,05.

20 Тело скользит по наклонной плоскости, образующей с горизонтом угол 45⁰ . Пройдя путь 36,4 см, тело приобретает скорость 2 м/с. Найти коэффициент трения тела о плоскость.

21 Маховик, момент инерции которого равен J=63,7 кг × м ² , вращается с постоянной угловой скоростью w =31,4 рад/с. Найти тормозящий момент М, под действием которого маховик останавливается через t=20 с. Маховик считать однородным диском.

22 Определить, какая постоянная касательная сила приложена к ободу однородного сплошного диска радиусом 0,5 м и массой 24 кг, если при вращении на него действует момент сил трения 2 Н × м . Угловое ускорение диска постоянно и равно 16 рад/ с² .

23 Маховое колесо, имеющее момент инерции 245 кг × м ² , вращается, делая 20 об/с. Через минуту после того, как на колесо перестал действовать вращающий момент, оно остановилось. Найти момент сил трения.

24 К ободу однородного сплошного диска радиусом R=0,2 м приложена постоянная касательная сила F=98,1 Н. При вращении на диск действует момент сил трения 5 Н × м . Найти массу диска, если известно, что диск вращается с постоянным ускорением e =100 рад/ с² .

25 Маховик в виде сплошного диска, момент инерции которого J=150 кг × м ² , вращается с частотой n =240 об/мин. Через время t=1 мин, как на маховик стал действовать момент сил торможения, он остановился. Определить момент сил торможения.

26 Вал массой m=100 кг и радиусом R=5 см вращался с частотой n =8 с^-1 . К цилиндрической поверхности вала прижали тормозную колодку с силой N=40 Н, под действием которой вал остановился через t=10 с. Определить коэффициент трения.

27 Диск массой m=2 кг и радиусом R=10 см вращается вокруг оси, проходящей через его центр. Уравнение движения диска имеет вид j = Сt ³, где С = -1рад / с³ . Определить вращающий момент М в момент времени t=2 с, если момент сил торможения постоянен и равен 12 Н × м .

28 Маховик радиусом 0,5 м, вращаясь равнозамедленно, за 10 секунд изменил частоту вращения от 480 до 120 об/мин. Тормозящий момент постоянен и равен 40 Н × м . Определить массу маховика.

29 К шару радиусом 0,2 м приложена касательная сила 100 Н. При вращении вокруг оси, проходящей через центр масс, на шар действует момент сил трения 5 Н × м . С каким угловым ускорением вращается шар, если его масса 15 кг?

30 Маховик в виде сплошного диска, момент инерции которого J=1,5 кг × м ² , вращаясь при торможении равнозамедленно, за время t=1 мин уменьшил частоту своего вращения с n₀ =240 об/мин до n₁=120 об/мин. Определить момент силы торможения.

31 На нитях одинаковой длины, равной 2,5 м, закрепленных в одной точке, подвешены два шарика массами 75 г и 100 г, соответственно. Нить с большим шариком отклонили на угол 60 градусов и отпустили. Считая удар абсолютно неупругим, определить, на какую высоту поднимутся шарики после соударения.

32 Пуля массой 15 г, летящая с горизонтальной скоростью 0,5 км/с, попадает в баллистический маятник массой 6 кг и застревает в нем. Определить высоту, на которую поднимется маятник, откачнувшись после удара.

33 Два тела массами 3 кг и 5 кг движутся навстречу друг другу со скоростями 7 м/с и 9 м/с. Найти скорость движения тел после соударения и выделившуюся при неупругом ударе энергию.

34 Пуля массой 15 г, летящая горизонтально со скоростью 200 м/с, попадает в баллистический маятник длиной 1 м и массой 1,5 кг и застревает в нем. Определить угол отклонения маятника.

35 Тело массой 3 кг движется со скоростью 2 м/с и ударяется о неподвижное тело такой же массы. Считая удар центральным и неупругим, определить количество теплоты, выделившееся при ударе.

36 Пуля массой 12 г, летящая с горизонтальной скоростью 0,6 км/с, попадает в мешок с песком массой 10 кг, висящий на длинной нити, и застревает в нем. Определить: 1) высоту, на которую поднимется мешок, отклонившись после удара; 2) энергию, израсходованную на пробивание песка.

37 На нитях одинаковой длины, равной 0,8 м, закрепленных в одной точке, подвешены два шарика массами 40 г и 60 г, соответственно. Нить с меньшим шариком отклонили на угол 60 градусов и отпустили. Считая удар неупругим, определить, какая энергия пошла на нагревание шариков.

38 Пуля массой 9 г, летящая с горизонтальной скоростью 0,6 км/с, попадает в баллистический маятник массой 8 кг и застревает в нем. Определить выделившуюся при этом энергию.

39 Тело массой 8 кг движется со скоростью 3 м/с и ударяется о движущееся со скоростью 1 м/с в том же направлении тело вдвое большей массы. Считая удар центральным и неупругим, определить количество теплоты, выделившееся при ударе.

40 На нитях одинаковой длины, равной 1,2 м, закрепленных в одной точке, подвешены стальной и пластилиновый шарики одного размера массой 20 г и 8 г, соответственно. Нить со стальным шариком отклонили на угол 45 градусов и отпустили. Определить, на какую высоту поднимутся шарики после соударения.

41 Определить скорость и ускорение материальной точки через 5 с после начала движения, если она совершает гармонические колебания, согласно уравнению x = 0,02 cos(pt + p / 3) , м. Написать уравнение для силы, вызывающей это движение, если масса точки 11 г.

42 Точка массой 20 г совершает гармонические колебания с амплитудой 10 см и периодом 5 с под действием некоторой периодической силы. Определить для точки максимальные скорость, ускорение и действующую силу.

43 Определить максимальную скорость точки, совершающей гармонические колебания по закону x = 3cos(pt / 2 + p / 8) , м. Найти массу этой точки, если максимальная сила, вызывающая эти колебания, равна 12 Н.

44 Скорость материальной точки, совершающей гармонические колебания, задается уравнением v(t) = -6 sin(2pt) , м/с. Записать зависимость смещения этой точки от времени. Найти силу, действующую на точку в момент времени t=6 с, если масса точки 4 г.

45 Определить скорость и ускорение материальной точки через 3 с после начала движения, если она совершает гармонические колебания согласно уравнению x = 0,02 cos(pt + p / 4) , м. Найти силу, действующую на точку через 20 с после начала движения, если масса точки 2 г.

46 Амплитуда гармонических колебаний материальной точки равна 5 см, период – 4 с. Найти максимальные скорость и ускорение колеблющейся точки. Найти силу, действующую на точку через 2 с после начала движения, если масса точки 10 г, а начальная фаза равна 120⁰.

47 Уравнение движения материальной точки  x = 2 sin(pt / 2 + p / 4) , см. Найти максимальную скорость точки и ее максимальное ускорение, а также силу, действующую на эту точку в начальный момент времени, если масса точки 7 г.

48 Уравнение движения материальной точки x = sin(pt / 6) , м. Найти моменты времени, в которые достигаются минимальные по модулю скорость и ускорение. Найти силу, действующую на точку через 10 с после начала движения, если масса точки 12 г.

49 Определить максимальные по модулю значения скорости и ускорения материальной точки, совершающей гармонические колебания с амплитудой 3 см и угловой частотой w = p/ 2 c^-1 . Найти силу, действующую на точку через 3 с после начала движения, если масса точки – 30 г, а начальная фаза колебаний – 60⁰.

50 Точка совершает колебания по закону  x = A cos(wt) , где А=5 см, w = 2c^-1. Определить ускорение точки в момент времени, когда ее скорость равна 8 см/с. Написать уравнение для силы, вызывающей это движение, если масса точки 9 г.

51 Азот, находившийся в состоянии 1 с параметрами  p₁=0,2  МПа, Т1 =450 К, V1 =2 л, изотермически перевели в состояние 2 с объемом V2 =6 л. Затем адиабатно объем газа был увеличен до V₃ =9 л. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.

52 Гелий, находящийся в состоянии 1 при давлении p₁=0,25 МПа, температуре   Т₁ =550 К и занимающий объем V₁=2,5 л, изобарно перевели в состояние 2 с температурой Т₂=650 К. Затем адиабатно объем газа был увеличен на 3 л. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.

53 Кислород, находящийся в состоянии 1 при давлении p₁=0,25 МПа, температуре Т₁ =550 К и занимающий объем V₁=2,5 л, изохорно перевели в состояние 2 с температурой Т₂=650 К. Затем адиабатно давление газа было уменьшено в 2 раза. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.

54 Водород, находящийся в состоянии 1 (p₁=0,1 МПа, Т1 =300 К, V1 =1 л), перевели в состояние 2, адиабатно уменьшив давление на 20%. Затем изобарно объем газа был увеличен до V₃ =2 л. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.

55 Гелий, находящийся в состоянии 1 ( р1 =310 кПа, Т1 =400 К, V1 =10 л), перевели в состояние 2, адиабатно увеличив давление в два раза. Затем изотермически объем газа был увеличен на 6 литров. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.

56 Кислород, находящийся в состоянии 1 (p₁=230 кПа, Т₁ =450 К, V₁ = 20 л), перевели в состояние 2, адиабатно уменьшив объем в три раза. Затем изохорно температура газа была увеличена на 100 К. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.

57 Кислород, находящийся в состоянии 1 при давлении p₁=250 кПа, температуре Т₁ =550 К и занимающий объем V₁=12 л, изотермически перевели в состояние 2 с объемом V₂ =6 л. Затем адиабатно объем газа был уменьшен на два литра. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.

58 Азот, находящийся в состоянии 1 при давлении p₁=220 кПа, температуре Т₁ =430 К и занимающий объем V₁=25 л, изобарно перевели в состояние 2, уменьшив объем на семь литров. Затем адиабатно давление газа было уменьшено на 30%. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.

59 Гелий, находящийся в состоянии 1 при давлении p₁=150 кПа, температуре Т₁ =500 К и занимающий объем V₁=12,5 л, изотермически перевели в состояние 2 с объемом 6,5 литра. Затем адиабатно температура газа была уменьшена на 100 К. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.

60 Водород, находящийся в состоянии 1 при давлении p₁=0,25 МПа, температуре Т₁ =550 К и занимающий объем V₁=2,5 л, изохорно перевели в состояние 2 с давлением р₂=0,5 МПа. Затем адиабатно объем газа был увеличен в 1,5 раза. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.

61 Электростатическое поле создано бесконечной заряженной плоскостью с поверхностной плотностью заряда  s = 1 мкКл/ м ² и точечным зарядом q = -2 мкКл, находящимся на расстоянии a = 0,5 м от плоскости. Определить напряженность поля в точке, находящейся на расстоянии r₁ = 0,5 м от плоскости и r₂ = 0,5 м от заряда.

62 Электрическое поле создано двумя концентрическими проводящими сферами   радиусами R1 =10 см и R 2 =90 см, несущими заряды q1 =2 нКл и q ₂ =1 нКл. Определить напряженность поля в точках на расстояниях r₁ = 80 см и r₂ = 1 м от центра сфер.

63 Электрическое поле создано двумя параллельными бесконечными плоскостями  с  поверхностными  плотностями  зарядов  150 мкКл/м²  и 240 мкКл/м², соответственно. Определить напряженность поля между плоскостями, справа и слева от плоскостей.

64 Электрическое поле создано двумя бесконечными параллельными нитями, заряженными с линейными плотностями t₁ =0,1 мкКл/м, t₂ =0,01 мкКл/м, находящимися на расстоянии а=10 см друг от друга. Определить напряженность поля в точке на расстоянии r₁=8 см от первой и r₂ =12 см от второй нити.

65 Электрическое поле создано бесконечной плоскостью с поверхностной плотностью заряда s =200 нКл/ м ² и бесконечной нитью с линейной плотностью t =0,1 мкКл/м, проходящей параллельно плоскости на расстоянии а=0,2 м. Определить напряженность поля в точке на расстоянии r₁=0,5 м от плоскости и r₂ =0,3 м от нити.

66 Электрическое поле создано бесконечной заряженной плоскостью с поверхностной плотностью заряда s = -1 мкКл/ м ² и точечным зарядом q = -2 мкКл, находящимся на расстоянии a = 0,5 м от плоскости. Определить напряженность поля в точке, расположенной на расстоянии r₁ = 0,2 м от плоскости и r₂ = 0,5 м от заряда.

67 Электрическое поле создано бесконечной заряженной нитью с линейной плотностью заряда t =100 мкКл/м и заряженной сферой радиусом R=0,2 м, с зарядом q = -500 мкКл. Расстояние между центром сферы и нитью а = 1 м. Определить  напряженность  поля  в точке, расположенной на расстоянии r1 =0,2 м от нити и r2 = 1,2 м от центра сферы.

68 Электрическое поле создано двумя концентрическими сферами радиусами R1 =10 см и R 2 =50 см, несущими заряды q1 =2 нКл и q 2 =-1 нКл. Определить напряженность поля в точках на расстояниях r₁=0,3 м, r₂ =1,4 м от центра сфер.

69 Электрическое поле создано двумя заряженными бесконечными нитями, лежащими в параллельных плоскостях и скрещенных под прямым углом. Линейные плотности зарядов нитей равны: t₁ = -0,2 мкКл/м, t₂ = 0,2 мкКл/м. Найти напряженность поля в точке, расположенной на расстоянии r₁ = 13 см от первой и r₂ = 5 см от второй нити. Расстояние между нитями d = 13 см.

70 Электрическое поле создано бесконечной плоскостью с поверхностной плотностью заряда s = - 200 нКл/ м ² и заряженной сферой радиусом R = 20 см, находящейся на расстоянии 0,5 м от плоскости. Заряд сферы q = 150 нКл. Определить напряженность поля в точке, одинаково удаленной от плоскости и центра сферы.

71 Вдоль силовой линии однородного электрического поля движется протон. В точке поля с потенциалом j₁=300 В протон имел скорость v₁ = 0,1 Мм/с. Определить: 1) потенциал j₂ точки поля, в которой скорость протона возрастает в 3 раза; 2) работу, которую при этом совершило поле.

72 Электрон, летевший горизонтально со скоростью v=1,6 Мм/с, влетел в однородное электрическое поле с напряженностью Е=90 В/см, направленной вертикально вверх. Какова будет по модулю и направлению скорость электрона через 1 нс? Какую работу совершило при этом поле?

73 Протон, начальная скорость которого равна 100 км/с, влетел в однородное электрическое поле в направлении линий напряженности. Какой путь должен пройти протон, чтобы его скорость удвоилась? Какую работу совершит при этом поле? Напряженность поля Е=300 В/см.

74 Пройдя ускоряющую разность потенциалов U=600 кВ, α-частица, летевшая со скоростью 5,4 Мм/с, увеличила свою скорость на 3,9 Мм/с. Заряд α-частицы равен 3,2 ×10^-19 Кл. Определить: 1) работу, совершенную полем при разгоне частицы; 2) удельный заряд α-частицы (отношение заряда к массе), считая массу неизвестной.

75 Пылинка массой m=1 пг, несущая на себе пять избыточных электронов, прошла в вакууме ускоряющую разность потенциалов 3 МВ. Найти: 1) изменение ее кинетической энергии; 2) работу сил поля; 3) изменение скорости пылинки. Начальная скорость пылинки 9 м/с.

76 Разность потенциалов между катодом и анодом электронной лампы равна 90 В, а расстояние между ними 24 мм. С каким ускорением движется электрон от катода к аноду? Какова скорость электрона в момент удара об анод? За какое время электрон пролетает расстояние от катода до анода? Какую работу при этом совершит электрическое поле лампы? Поле считать однородным.

77 Какой путь пройдет электрон в однородном электрическом поле напряженностью Е = 200 кВ/м вдоль силовой линии за время t = 1 нс, если его начальная скорость была равна нулю? Какими скоростью и кинетической энергией будет обладать электрон в конце заданного интервала времени? Какую работу при этом совершит электрическое поле?

78 Вдоль силовой линии однородного электрического поля движется α-частица. В точке поля с потенциалом j₁ = 120 В  α-частица имела скорость v₁ = 50 км/с. Определить: 1) потенциал j ₂ точки поля, в которой ее скорость возрастет в 2 раза; 2) работу, которую при этом совершило поле.

79 Электрон с начальной скоростью v₀ = 3 Мм/с влетел в однородное электрическое поле напряженностью Е=150 В/м. Вектор начальной скорости перпендикулярен линиям напряженности электрического поля. Найти: 1) силу F, действующую  на  электрон;  2) ускорение, приобретенное электроном; 3) скорость электрона через t=0,1 мкс; 4) работу, совершенную при этом полем.

80 Протон, летевший горизонтально со скоростью v = 0,6 Мм/с, влетел в однородное электрическое поле с напряженностью Е = 120 В/см, направленной вертикально вверх. Какова будет по модулю и направлению скорость протона через 1 мкс? Какую работу совершит поле при таком изменении скорости?

81 Батарея, состоит из трех включенных параллельно одинаковых источников тока с ЭДС e = 12,2 В и внутренним сопротивлением r = 3 Ом каждый. Соединенная с ней внешняя электрическая цепь имеет сопротивление R=24 Ом. Определить: 1) полезную мощность; 2) наибольшую мощность, которую можно получить во внешней цепи.

82 ЭДС источника тока e = 2 В, внутреннее сопротивление r = 1 Ом. Определить силу тока, если внешняя цепь потребляет мощность Р = 0,75 Вт. Какую наибольшую мощность можно получить во внешней цепи?

83 Определить силу тока короткого замыкания Iкз  для аккумуляторной батареи, если при токе нагрузки I₁ = 5А она отдает во внешнюю цепь мощность P₁ = 9,5 Вт, а при токе нагрузки в 8 А – P₂ = 14,4 Вт. Какую наибольшую мощность можно получить во внешней цепи?

84 Батарея состоит из трех одинаковых включенных последовательно источников тока с ЭДС e = 2,2 В и внутренним сопротивлением r = 1 Ом каждый. Соединенная с ней внешняя электрическая цепь имеет сопротивление R=48 Ом. Определить: 1) полезную мощность; 2) наибольшую мощность, которую можно получить во внешней цепи.

85 Батарея состоит из пяти последовательно соединенных элементов с ЭДС e = 1,4 В и с внутренним сопротивлением r = 0,3 Ом каждый. При каком сопротивлении внешней нагрузки полезная мощность равна Р = 8 Вт ? Какую наибольшую мощность можно получить во внешней цепи?

86 Аккумулятор с внутренним сопротивлением r = 0,08 Ом при токе нагрузки I₁ = 4 А отдает во внешнюю цепь мощность P₁ = 8 Вт. Какую мощность P₂ отдаст он во внешнюю цепь при токе нагрузки I ₂ = 6 А? Какую наибольшую мощность можно получить во внешней цепи?

87 Элемент питания замыкают сначала на внешнее сопротивление R₁=2 Ом, а затем на внешнее сопротивление R ₂ =0,5 Ом. Найти ЭДС элемента и его внутреннее сопротивление, если известно, что в каждом из этих случаев, мощность, выделяемая во внешней цепи, одинакова и равна 2,54 Вт. Какую наибольшую мощность можно получить во внешней цепи?

88 Два источника тока с ЭДС 24 В и с внутренними сопротивлениями 2 Ом и 3 Ом соединены параллельно. При каком сопротивлении внешней нагрузки полезная мощность равна 64 Вт? Какую наибольшую мощность можно получить во внешней цепи?

89 Лампочка и реостат, включенные последовательно, присоединены к источнику тока с внутренним сопротивлением 2 Ом. Напряжение на зажимах лампочки равно 40 В, сопротивление реостата равно 10 Ом. Внешняя цепь потребляет мощность 120 Вт. Найти силу тока в цепи. Какую наибольшую мощность можно получить во внешней цепи?

90 Батарея состоит из трех параллельно соединенных источников тока с ЭДС e = 12 В и с внутренним сопротивлением r = 2 Ом каждый. При каком сопротивлении внешней нагрузки полезная мощность равна 32 Вт? Какую наибольшую мощность можно получить во внешней цепи?

В задачах 91-100, с использованием правил Кирхгофа, найти силы токов на всех участках цепи и разность потенциалов между узлами.

В задаче известно: e₁ =2,5 В, e₂ =2,2 В, e3 =3,0 В, r1 = r 2 = r 3 = 0,2 Ом, R = 4,7 Ом.