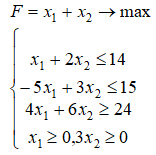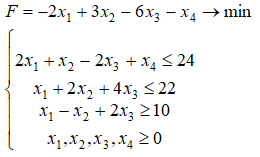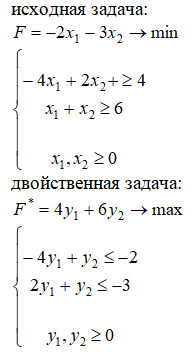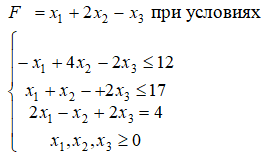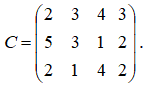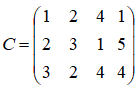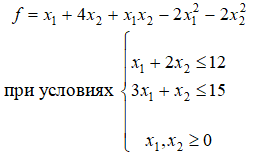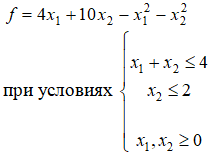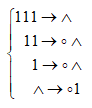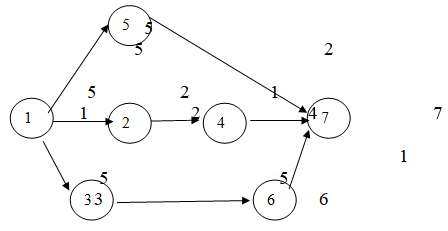
КОМПЛЕКТ ТЕСТОВЫХ ЗАДАНИЙ.

Вариант 1

Задание 1

В канонической задаче ЛП ограничения записаны в виде:

А) неравенств

Б) равенств

В) равенств и неравенств

Задание 2

Дана задача оптимального планирования производства:

F=2х₁+3х₂ → max

х₁+4х₂≤14

3х₁+4х₂≤18

6х₁+2х₂≤27

х₁≥0, х₂≥0

составить двойственную задачу

a) q =14y₁+18y₂+27y₃ → min

y₁+3y₂+6y₃≥2

4y₁+4y₂+2y₃≥3

y₁≥0, y₂≥0, y₃≥0

б) q=y₁+3y₂+6y₃ → min

2y₁+3y₂≥2

4y₁+4y₂≥3

y₁≥0, y₂≥0, y₃≥0

в) q=4y₂+4y₃ → min

14y₁+18y₂≥15

y₁+3y₂+6y₃≥2

y₁≥0, y₂≥0, y₃≥0

Задание 3

Найти критический путь в сетевом графике.

а) 1-3-6-7

б) 1-2-4-7

в)1-5-7

Задание 4

Максимизировать линейную форму α=2х₁+2х₂ при ограничениях

3х₁-2х₂≥-6

3х₁+х₂≥3

х₁≤3

а) 10

б) 21

в) 15

Задание 5

Составить начальный план перевозок методом северо-западного угла в транспортной задаче.

а)

б)

в)

Вариант 2

Задание 1

В стандартной задаче ЛП ограничения записаны в виде:

а) неравенств и равенств

б) равенств

в) неравенств

Задание 2

Дана задача оптимального планирования производства:

F=6х₁+4х₂+5х₃+8х₄ → max

х₁+2х₂+х₃+5х₄≤80

6х₁+5х₂+4х₃+2х₄≤80

4х₁+6х₂+7х₃+2х₄≤80

х₁≥0, х₂≥0, х₃≥0, х₄≥0

составить двойственную задачу

а) q =4y₁+6y₂+7y₃+2y₄ → min

y₁+6y₂+4y₃+≤6

y₁+4y₂+7y₃≤5

5y₁+2y₂+2y₃≤8

Yi≥0, i=1,2,3

б) q =80y₁+50y₂+100y₃ → min

y₁+6y₂+4y₃+≤6

2y₁+5y₂+6y₃≤4

y₁+4y₂+7y₃≤5

5y₁+2y₂+2y₃+≤8

Yi≥0, i=1,2,3

в) q =6y₁+5y₂+4y₃+2y₄ → min

y₁+6y₂+4y₃+≤6

5y₁+2y₂+2y₃≤4

Yi≥0, i=1,2,3

...................

ТИПОВЫЕ ЗАДАЧИ

1. Найдите точки экстремума функции z =x²+ y² при условии 3х+2у=1, используя метод множителей Лагранжа.

2. Решите задачу линейного программирования графическим способом:

3. Решите задачу симплекс-методом:

4. Найдите решение двойственной пары задач:

5. Для задачи, состоящей в определении максимального значения функции

составить двойственную задачу и найти ее решение.

6.  Предприятие выпускает два вида продукции П₁ и П₂. Для выпуска каждого вида продукции требуется 4 вида ресурсов: Р₁, Р₂, Р₃, Р₄. Объем ресурсов вида P_i, которыми располагает предприятие, равен b_i (i=1,2,3,4). Цена 1 единицы продукции вида П_j  равна С_j (j = 1,2). Объемы ресурсов каждого вида P_i, используемых при выпуске 1 единицы продукции вида П_j,  указаны в таблице. Сколько продукции каждого вида нужно выпустить, чтобы общая стоимость выпущенной продукции была максимальной?

Требуется:

а) решить задачу графическим методом;

б) решить задачу симплексным методом, поставить двойственную задачу, найти ее решение и проверить правильность решения прямой и двойственной задачи с помощью теоремы двойственности;

в) дать экономическую интерпретацию решений прямой и двойственной задач.

7. При откорме животных каждое животное ежедневно должно получить не менее 60 ед. питательного вещества А, не менее 50 ед. питательного вещества В и не менее 12 ед. вещества С. Указанные питательные вещества содержат три вида корма. Содержание единиц питательных веществ в 1кг каждого из видов корма приведено в таблице:

Составьте дневной рацион, обеспечивающий получение необходимого количества питательных веществ, при минимальных денежных затратах, если цена 1 кг корма 1 вида составляет 9 руб., корма 2 вида – 12 руб., корма 3 вида – 10 руб.

8. На трех складах оптовой базы сосредоточен однородный груз в количествах 90, 60 и 150 ед. Этот груз необходимо перевезти в 4 магазина. Каждый из магазинов должен получить соответственно 120, 40, 60 и 80 ед. груза. Тарифы перевозок ед. груза из каждого из складов во все магазины задаются матрицей:

Составьте такой план перевозок, при котором общая стоимость перевозок является минимальной. План перевозок транспортной задачи построить методом северо-западного угла.

9. Производственное объединение имеет в своем составе три филиала, которые производят однородную продукцию соответственно в количествах, равных 50, 30 и 10 ед. Эту продукцию получают четыре потребителя, расположенные в разных местах. Их потребности соответственно равны 30, 30, 10 и 20 ед. Тарифы перевозок ед. продукции от каждого из филиалов соответствующим потребителям задаются матрицей:

Составьте такой план прикрепления получателей продукции к ее поставщикам, при котором общая стоимость перевозок является минимальной. План решения транспортной задачи построить методом наименьшей стоимости.

10. Решите задачу выпуклого программирования. Найдите максимальное значение функции 

11. Решите задачу, используя градиентные методы. Найдите максимальное значение функции 

12. Составить математическую модель, записать уравнение Беллмана и решить графически следующие задачи на определение оптимальных сроков замены оборудования. Даны: первоначальная стоимость оборудования p₀, его ликвидная стоимость j(t), стоимость содержания r(t) в течение года оборудования возраста t лет, n – срок эксплуатации, в конце которого оборудование продается. Критерий оптимальности – суммарные затраты на эксплуатацию оборудования в течение n лет с учетом первоначальной покупки и последующей продажи.

p₀ = 8000; n = 5; j(t) и r(t) заданы таблично:

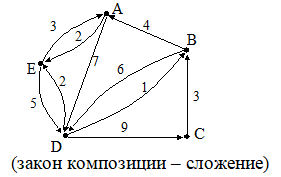
13. Найти максимальный и минимальный пути длины 3 с началом в вершине А через дуги графа:

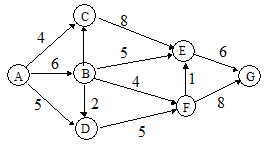
14. Найти максимальный и минимальный пути из вершины А в вершину G в графе со значениями на дугах

a) с помощью алгоритма Форда;

b)     

c) c помощью алгоритма Беллмана-Калаба.

15. Нормальный алгоритм Маркова в алфавите А={1} определяется следующей схемой подстановок:

где ^ – пустое слово, а точка в правой части означает завершение выполнения шагов алгоритма (заключительная подстановка).

Охарактеризовать функцию ..., вычисляемую этим алгоритмом.

16. Телефонная компания по производству и продаже телефонов может производить сама или закупать компоненты для телефонных аппаратов. Прогнозируемые оценки прибылей (в у.е.) за год, зависящих от уровней продаж приведены в таблице (вероятности каждого из  четырех уровней продаж равны соответственно 0,1; 0,2; 0,6; 0,1).

Построить дерево решений и произвести его оценку. Какое решение следует принять руководству компании – о собственном производстве или о закупке компонент?

17. Инвестиционный банк получил предложение инвестировать 3 млн. руб. Первое предложение – вложить деньги в облигации с 7,3% годового дохода. Второе – купить земельный участок. Местные власти хотят на этом участке развивать промышленность, что может дать в будущем 17% дохода. Однако, эта земля возможно будет занята под строительство автодороги, в этом случае власти вернут банку 4,5% сверх цены покупки участка. Вероятности будущих решений местных властей неизвестны.

Что можно посоветовать банку?

18. Предприятие выпускает и продает свежие горячие батоны. Уровень спроса на них колеблется от 200 до 280 батонов  в день. Менеджер может принять решения: А₁ – выпечь 200 батонов, А₂ – выпечь 240 батонов и А₃ – выпечь 270 батонов. Средний уровень спроса – 240 батонов, примем еще два уровня спроса – 210 батонов и 270. Себестоимость каждого батона 4 рубля, цена горячего свежего батона – 6 рублей. Батоны, не проданные горячими в конце дня, продаются по 3 рубля за штуку. В том случае, когда батонов не хватает (спрос превысил предложение), следует штраф  2 рубля за каждый батон.

Требуется:

а) сформировать таблицу решений;

б) найти оптимальные решения по критериям Лапласа, пессимиста, оптимиста, Гурвица (a = 0,6), Cэвиджа.