| Общая информация » Каталог студенческих работ » ОНЛАЙН ТЕСТЫ » Методы оптимальных решений |
| 27.01.2013, 22:09 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1. Выражение базисных неизвестных через свободные называется … решением. 2. Дана совместная система из m линейных уравнений с n неизвестными, где m<n, m>=2. Ранг матрицы системы равен числу уравнений, тогда число базисных решений равно: 3. Для получения нового коэффициента необходимо из произведения элементов главной диагонали вычесть произведение элементов побочной диагонали, затем полученный результат… 4. Дано общее решение системы линейных уравнений
Соответствующее ему базисное решение имеет вид: 5. Даны базисные векторы 6. Дана система линейных неравенств
Минимальное значение функции при данных ограничениях равно: 7. Дана симплекс-таблица для задачи на минимум.
Наибольшая величина убывания функции равна: 8. В задаче линейного программирования на минимум искусственная переменная входит в целевую функцию с коэффициентом: 9. Если в оптимальном плане расширенной задачи не все искусственные переменные равны нулю, то исходная задача имеет: 10. Дана симплекс-таблица для задачи на максимум
Оптимальный план имеет вид: 11. В транспортной задаче m поставщиков n потребителей, тогда число переменных равно: 12. Для оптимальности плана 13. Если m - число поставщиков, n - число потребителей, то ранг матрицы системы ограничений-уравнений закрытой транспортной задачи равен: 14. Метод нахождения оптимального плана закрытой транспортной задачи: 15. Установите соответствие между опорными планами транспортных задач и оценками этих планов
Оценки
16. В транспортной задаче на сети m вершин и n ребер. Количество базисных ребер равно: 17. В транспортной задаче на сети решение оптимально, если оценки 18. В цикле пересчета транспортной задачи на сети разрешающая стрелка направлена: 19. Величина корректировки плана в сетевой задаче равна: 20. Переход от одного плана к другому в сетевой задаче осуществляется следующим образом: 21. Задача о назначениях. Венгерский метод. Если незанятых нулей нет, то… 22. Задача о назначениях. Венгерский метод. Количество 23. Задача о назначениях. Венгерский метод. Цепочка состоит из одного нуля со штрихом, если в данном столбце: 24. Задача о назначениях. Венгерский метод. Цепочка из нулей: 25. Задача о назначениях. Венгерский метод. Переход от одного неполного выбора нулей к другому осуществляется следующим образом: 26. Метод нахождения оптимального плана транспортной задачи с ограниченными пропускными способностями: 27. Для оптимальности плана 28. Дан произвольный опорный план транспортной задачи с ограничениями на пропускные способности.
При переходе к новому плану издержки на перевозку уменьшаться на: 29. Дана транспортная задача с ограниченными пропускными способностями коммуникаций
Для некоторого плана известны оценки
Минимальные издержки на перевозку всей продукции равны: 30. Дана транспортная задача с ограничениями на пропускные способности
Для некоторого плана по формуле Опорный план имеет вид: 31. . Для платёжной матрицы 32. Для платёжной матрицы 33. Дана матричная игра 34. Дана матричная игра 35. Дана матричная игра | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

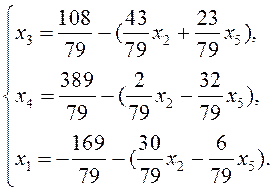
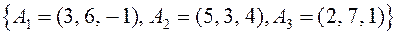 . Разложение вектора
. Разложение вектора 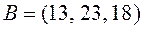 по векторам базиса
по векторам базиса 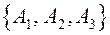 имеет вид:
имеет вид: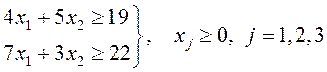 и функция
и функция 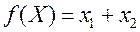 .
.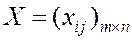 закрытой транспортной задачи необходимо и достаточно существование чисел
закрытой транспортной задачи необходимо и достаточно существование чисел 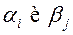 таких, что:
таких, что: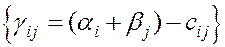 :
: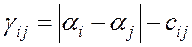 небазисных ребер:
небазисных ребер: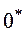 в цепочке должно быть:
в цепочке должно быть: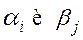 таких, что выполняются условия:
таких, что выполняются условия: 5
5 3
3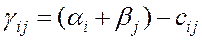 .
. 11
11 9
9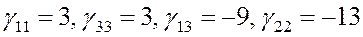 . Где
. Где 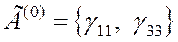 ,
, 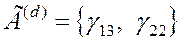 .
.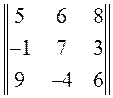 нижняя цена игры равна:
нижняя цена игры равна: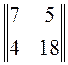 цена игры равна:
цена игры равна: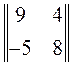 . Вероятность выбора первой стратегии первым игроком равна:
. Вероятность выбора первой стратегии первым игроком равна: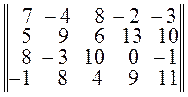 . После исключения доминируемых стратегий размерность платёжной матрицы будет равна:
. После исключения доминируемых стратегий размерность платёжной матрицы будет равна: