Структура контрольной работы

1. Титульный лист.

2. Введение

3. Основная часть.

4. Заключение.

5. Список использованных литературных источников.

Теоретические вопросы

1. Общие сведения о теории надежности систем электроснабжения. Понятия, термины и определения в теории надежности. Объекты, свойства, состояния и события.

2. Основные сведения из теории вероятностей и математической статистики. События. Вероятность события.

3. Теорема сложения и умножения вероятностей. Законы распределения случайных величин.

4. Виды, типы и классификация отказов.

5. Требования к надежности электроснабжения потребителей электрической энергии. Классификация электроприемников и потребителей по степени последствий от нарушений электроснабжения.

6. Основные показатели надежности. Единичные показатели для невосстанавливаемых и восстанавливаемых объектов.

7. Комплексные показатели надежности объектов. Коэффициенты готовности, оперативной готовности, вынужденного простоя, технического использования.

8. Надежность систем с последовательным и параллельным соединением элементов. Надежность систем со смешанным соединением элементов. Мостиковая структура.

9. Классификация методов резервирования систем электроснабжения. Расчет надежности систем при постоянном общем и раздельном резервировании. Резервирование с дробной кратностью.

10. Надежность резервируемых, нерезервируемых и автоматизируемых сетей систем электроснабжения.

11. Надежность систем со смешанным соединением элементов. Приближенный метод преобразования треугольника в звезду и обратно.

12. Понятия о структурной и функциональной надежности сложных электроэнергетических систем.

13. Математические модели надежности сложных схем электроснабжения на основе метода минимальных путей и сечений.

14. Математические модели отказов и восстановления элементов СЭС на основе метода Марковских случайных процессов.

15. Влияние надежности коммутационной аппаратуры и устройств релейной защиты и автоматики на надежность схем электроснабжения.

16. Технико-экономическая оценка недоотпуска электроэнергии

17. Экономический эффект от повышения надежности.

18. Влияние качества электроэнергии на надежность.

19. Повышение надежности работы электрооборудования.

20. Практические рекомендации по повышению надежности систем электроснабжения.

Задание 1

Применение основных формул и теорем теории вероятностей для решения задач надежности

Задача 1

1. В РП установлено пять автоматических выключателей, при их исправном состоянии обеспечивается нормальная работа потребителей. При монтаже РП выключатели выбирались из партии объемом в 1000 штук, в которой было 950 исправных выключателей и 50 не исправных. Найти вероятность исправной работы РП.

2. В мастерской находится 4 пускателя, прошедших испытания на надежность, и 5 неиспытанных. Наугад из этого общего количества взяли два пускателя. Найти вероятность того, что один из них испытан, а другой нет.

3. В электроустановке четыре блокировки, срабатывающие в определенной последовательности. Каждая последующая ступень срабатывает при отказе предыдущей. Найти вероятность того, что сработает первая ступень, вторая ступень, третья ступень и четвертая ступень при условии, что вероятности исправной работы каждой отдельно взятой блокировки составляют: 0,92; 0,95; 0,96; 0,96.

4. Устройство состоит из пяти элементов, из которых два изношены. При включении устройства включаются случайным образом два элемента. Найти вероятность того, что включенными окажутся неизношенные элементы.

5. Имеется партия из 50 деталей, причем 20 из них бракованные. Из этой партии выбирают 10 деталей, а затем из этих 10 деталей для контроля выбирается 1 деталь. Если эта деталь исправна, то партия проходит проверку. Найти вероятность того, что партия будет принята.

6. На предприятии брак представляет 1,5 % от общего выпуска изделий. Общий выпуск изделий первого сорта из небракованных составляет 80 %. Какова вероятность того, что взятое наугад изделие окажется изделием первого сорта, если оно взято из общей массы изготавливаемой продукции.

7. Вероятность того, что расход электроэнергии в продолжение одних суток не превысит установленной нормы, равна 0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.

8. В электрическую цепь последовательно включены три элемента, работающие независимо один от другого. Вероятность отказов первого, второго и третьего элементов соответственно равны: p1 = 0,1; p2 = 0,15; p3 = 0,2. Найти вероятность того, что тока в цепи не будет.

9. Две цепи электроснабжения работают параллельно на общую нагрузку. Вероятность аварийного простоя одной цепи q1 = 0,6×10^-3 , второй q2 = 0,8×10^-3. Принимая аварийные состояния цепей независимыми, определить вероятность аварийного простоя двухцепной электропередачи для двух случаев:

а) отказ электропередачи происходит при отказе одной из цепей (любой);

б) отказ электропередачи происходит при отказе только обеих цепей.

10. Двадцать экзаменационных билетов содержат по два неповторяющихся вопроса. Экзаменуемый студент знает ответы на 35 вопросов. Найти вероятность того, что экзамен будет сдан, если для этого достаточно ответить на два вопроса одного билета или на один вопрос билета и один дополнительный вопрос из других билетов.

Задача 2. Варианты исходных данных для решения задач выбираются согласно последней цифре номера зачетной книжки по таблице 1.1.

Таблица 1.1 Исходные данные по вариантам

Задание 2

Применение основных формул для определения резервирования

Условие задачи для всех вариантов: Основная система содержит (Х) равнонадежных элемента с логически последовательным соединением с вероятностью безотказной работы р_i.

Вариант 1

Х=3

Интенсивность отказа одного элемента λ = 0,2 × 10^-3 (1/ч). Определить вероятность безотказной работы системы и отказа в течение 60 часов при общем резервировании системы. Изобразить структурную схему системы

1. Без резервирования;

2. При общем резервировании;

3. При раздельном резервировании

Вариант 2.

Х=4

Интенсивность отказа одного элемента λ = 0,3 ×10 ^-3 (1/ч). Определить вероятность безотказной работы системы и отказа в течение 80 часов при поэлементном резервировании системы. Изобразить структурную схему системы.

1. Без резервирования;

2. При общем резервировании;

3. При раздельном резервировании;

Вариант 3

Х=4

Интенсивность отказа одного элемента λ = 0,005 час^-1. Определить вероятность безотказной работы системы и отказа в течение 70 часов при поэлементном резервировании системы. Изобразить структурную схему системы.

1. Без резервирования;

2. При общем резервировании;

3. При раздельном резервировании.

Вариант 4

Х=3

Интенсивность отказа одного элемента  λ = 0,35 ×10 ^-3 (1/ч). Определить вероятность безотказной работы и отказа системы. Изобразить структурную схему системы. в течение 56 часов при поэлементном резервировании системы.

1. Без резервирования;

2. При общем резервировании;

3. При раздельном резервировании.

Вариант 5

Х=4

Интенсивность отказа одного элемента λ = 0,42 ×10 ^-3 (1/ч). Определить вероятность безотказной работы системы и отказа в течение 90 часов при поэлементном резервировании системы. Изобразить структурную схему системы.

1. Без резервирования;

2. При общем резервировании;

3. При раздельном резервировании;

Вариант 6

Х=5

Интенсивность отказа одного элемента λ = 0,64 ×10 ^-3 (1/ч). Определить вероятность безотказной работы системы и отказа в течение 60 часов при поэлементном резервировании системы. Изобразить структурную схему системы

1. Без резервирования;

2. При общем резервировании;

3. При раздельном резервировании

Вариант 7

Х=3

Интенсивность отказа одного элемента λ = 0,075 (1/ч). Определить вероятность безотказной работы системы и отказа в течение 80 часов при поэлементном резервировании системы. Изобразить структурную схему системы

1. Без резервирования;

2. При общем резервировании;

3. При раздельном резервировании;

Вариант 8

Х=4

Интенсивность отказа одного элемента λ = 0,65 ×10 ^-2 (1/ч). Определить вероятность безотказной работы системы и отказа в течение 60 часов при общем резервировании системы. Изобразить структурную схему системы.

1. Без резервирования;

2. При общем резервировании;

3. При раздельном резервировании;

Вариант 9

Х=3

Интенсивность отказа одного элемента λ = 0,006(1/ч). Определить вероятность безотказной работы системы и отказа в течение 80 часов при поэлементном резервировании системы. Изобразить структурную схему системы

1. Без резервирования;

2. При общем резервировании;

3. При раздельном резервировании.

Вариант 10

Х=5

Интенсивность отказа одного элемента λ = 0,058 (1/ч). Определить вероятность безотказной работы системы и отказа в течение 80 часов при общем резервировании системы. Изобразить структурную схему системы.

1. Без резервирования;

2. При общем резервировании;

3. При раздельном резервировании;

Вариант 11

Х=3

Интенсивность отказа одного элемента λ = 0,0075 (1/ч). Определить вероятность безотказной работы системы и отказа в течение 66 часов при поэлементном резервировании системы. Изобразить структурную схему системы.

1. Без резервирования;

2. При общем резервировании;

3. При раздельном резервировании.

Вариант 12

Х=4

Интенсивность отказа одного элемента λ = 0,005 (1/ч). Определить вероятность безотказной работы системы и отказа в течение 80 часов при общем резервировании системы. Изобразить структурную схему системы.

1. Без резервирования;

2. При общем резервировании;

3. При раздельном резервировании

Вариант 13

Х=5

Интенсивность отказа одного элемента λ = 0,0065 (1/ч). Определить вероятность безотказной работы системы и отказа в течение 60 часов при поэлементном резервировании системы.. Изобразить структурную схему системы.

1. Без резервирования;

2. При общем резервировании;

3. При раздельном резервировании

Вариант 14

Х=3

Интенсивность отказа одного элемента λ = 0,035 (1/ч). Определить вероятность безотказной работы системы и отказа в течение 60 часов при общем резервировании системы.. Изобразить структурную схему системы.

1. Без резервирования;

2. При общем резервировании;

3. При раздельном резервировании

Вариант 15

Х=3

Интенсивность отказа одного элемента λ = 0,009 (1/ч). Определить вероятность безотказной работы системы и отказа в течение 70 часов при поэлементном резервировании системы.. Изобразить структурную схему системы.

1. Без резервирования;

2. При общем резервировании;

3. При раздельном резервировании.

Вариант 16

Х=4

Интенсивность отказа одного элемента λ = 0,05 (1/ч). Определить вероятность безотказной работы системы в течение 50 часов при поэлементном резервировании системы. Изобразить структурную схему системы.

1. Без резервирования;

2. При общем резервировании;

3. При раздельном резервировании

Вариант 17

Х=5

Интенсивность отказа одного элемента λ = 0,2 × 10^-3 (1/ч). Определить вероятность безотказной работы системы и отказа в течение 80 часов при общем резервировании системы. Изобразить структурную схему системы.

1. Без резервирования;

2. При общем резервировании;

3. При раздельном резервировании.

Вариант 18

Х=3

Интенсивность отказа одного элемента λ = 0,0067 (1/ч). Определить вероятность безотказной работы системы и отказа в течение 60 часов при поэлементном резервировании системы. Изобразить структурную схему.

1. Без резервирования;

2. При общем резервировании;

3. При раздельном резервировании;

Вариант 19

Х=4

Интенсивность отказа одного элемента λ = 0,075 (1/ч). Определить вероятность безотказной работы системы и отказав течение 75 часов при общем резервировании системы. Изобразить структурную схему системы.

1. Без резервирования;

2. При общем резервировании;

3. При раздельном резервировании.

Вариант 20

Х=5

Интенсивность отказа одного элемента λ = 0,25 ×10 ^-3 (1/ч). Определить вероятность безотказной работы системы и отказа в течение 60 часов при поэлементном резервировании системы. Изобразить структурную схему системы.

1. Без резервирования;

2. При общем резервировании;

3. При раздельном резервировании.

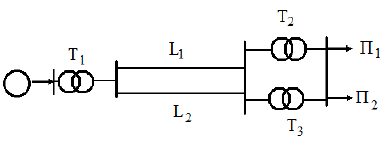
Задание 3

Применение основных формул для определения ущерба от недоотпуска электроэнергии потребителей

Задача: условие задачи для всех вариантов одинаково.

Определить параметр потока отказов системы электроснабжения, среднее время безотказной работы, среднюю вероятность отказа, среднее время восстановления, а также недоотпуск электроэнергии за год.

Вариант 1.  Мощность потребителей Р₁ = 70 МВт и Р₂ = 60 МВт величина удельного ущерба y_t = 0,25 руб. / кВтч

Рис. Схема электроснабжения

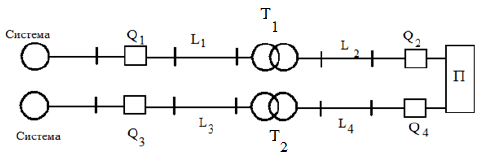
Вариант 2.  Мощность потребителей Р1 = 70 МВт. Величина удельного ущерба y_t = 0,25 руб / кВтч, а параметры L₃=L₄ =45 км.

Рис. Схема электроснабжения

.....