| Общая информация » Каталог студенческих работ » ТЕХНИЧЕСКИЕ ДИСЦИПЛИНЫ » Информационные системы в экономике |
| 24.10.2013, 09:41 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
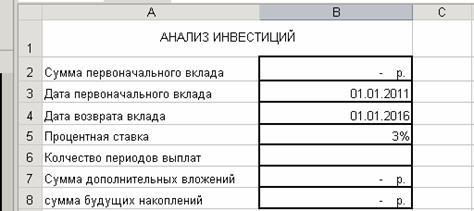
КОНТРОЛЬНАЯ РАБОТА № 1 По дисциплине «Информационные системы в экономике» Выполнение контрольных работ предусмотрено ГОС по дисциплине «Информационные системы в экономике». Необходимо выполнить все лабораторные работы одну за другой. 1. Выполнение лабораторного практикума ЛАБОРАТОРНАЯ РАБОТА № 1 Финансовые функции для расчетов по кредитам, займам, оценкам инвестиций с помощью табличного процессора Excel Финансовые вычисления включают в себя совокупность методов и расчетов, используемых при принятии управленческих решений. 1. Технология работы: встроенные финансовые функции Excel рассматриваются НА КОНКРЕТНЫХ ПРИМЕРАХ 2. Запустите электронную таблицу Excel. Присвойте данному файлу имя – Информационные системы, а Лист1 переименуйте в – Финансовые функции. Все задачи сохранять на данном листе. ОПИСАНИЕ ФУНКЦИЙ: 1) ПС – возвращает приведенную (к текущему моменту) стоимость инвестиции. Приведенная (нынешняя) стоимость представляет собой общую сумму, которая на настоящий момент равноценна ряду будущих выплат. Например, когда вы занимаете деньги, сумма займа является приведенной (нынешней) стоимостью для заимодавца. ПС(Ставка;Кпер;Плт;Бс;Тип), где Ставка – процентная ставка за период; Кпер – общее число периодов платежей по аннуитету; Плт — выплата, производимая в каждый период и не меняющаяся за все время выплаты ренты. Обычно выплаты включают основные платежи и платежи по процентам, но не включают других сборов или налогов; Бс – требуемое значение будущей стоимости или остатка средств после последней выплаты; Тип – число 0 или 1, обозначающее, когда должна производиться выплата. 2) КПЕР – возвращает общее количество периодов выплаты для инвестиции на основе периодических постоянных выплат и постоянной процентной ставки. КПЕР(ставка;плт;пс;бс;тип), где, Ставка — процентная ставка за период; Плт — выплата, производимая в каждый период; это значение не может меняться в течение всего периода выплат. Обычно платеж состоит из основного платежа и платежа по процентам и не включает налогов и сборов; Пс —приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей; Бс — требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент бс опущен, то он полагается равным 0; Тип — число 0 или 1, обозначающее, когда должна производиться выплата. 3) СТАВКА – возвращает процентную ставку по аннуитету за один период. СТАВКА(кпер;плт;пс;бс;тип;предположение) где, Кпер — общее число периодов платежей по аннуитету; Плт — регулярный платеж (один раз в период), величина которого остается постоянной в течение всего срока аннуитета. Обычно плт состоит из платежа основной суммы и платежа процентов, но не включает других сборов или налогов. Если аргумент опущен, должно быть указано значение аргумента бс; Пс — приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей; Бс — требуемое значение будущей стоимости или остатка средств после последней выплаты.; Тип — число 0 или 1, обозначающее, когда должна производиться выплата. 4) ПЛТ – Возвращает сумму периодического платежа для аннуитета на основе постоянства сумм платежей и постоянства процентной ставки. ПЛТ(ставка;кпер;пс;бс;тип), где, Ставка — процентная ставка по ссуде: Кпер — общее число выплат по ссуде; Пс — приведенная к текущему моменту стоимость, или общая сумма, которая на текущий момент равноценна ряду будущих платежей, называемая также основной суммой; Бс — требуемое значение будущей стоимости, или остатка средств после последней выплаты. Если аргумент бс опущен, то он полагается равным 0 (нулю), т. е. для займа, например, значение бс равно 0; Тип — число 0 (нуль) или 1, обозначающее, когда должна производиться выплата 5) ПРПЛТ – возвращает сумму платежей процентов по инвестиции за данный период на основе постоянства сумм периодических платежей и постоянства процентной ставки. Для получения более полного описания смысла аргументов функции ПРПЛТ и более подробной информации о функциях, связанных с ежегодными выплатами, см. справку по функции ПС. ПРПЛТ(ставка;период;кпер;пс;бс;тип) где, Ставка — процентная ставка за период; Период — это период, для которого требуется найти платежи по процентам; должен находиться в интервале от 1 до «кпер»; Кпер — общее число периодов выплат годовой ренты; Пс — приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей; Бс — требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент бс опущен, то он полагается равным 0 (например, бзс для займа равно 0); Тип — число 0 или 1, обозначающее, когда должна производиться выплата. Если аргумент «тип» опущен, то он полагается равным 0. 6) ОСПЛТ – возвращает величину платежа в погашение основной суммы по инвестиции за данный период на основе постоянства периодических платежей и постоянства процентной ставки. ОСПЛТ(ставка;период;кпер;пс;бс;тип) где, Ставка — процентная ставка за период; Период — задает период, значение должно быть в интервале от 1 до «кпер»; Кпер — общее число периодов выплат годовой ренты; Пс — приведенная стоимость, т. е. общая сумма, которая равноценна ряду будущих платежей; Бс — требуемое значение будущей стоимости, или остатка средств после последней выплаты. Если аргумент бс опущен, то он полагается равным 0 (нулю), т. е. для займа, например, значение бс равно 0; Тип — число 0 или 1, обозначающее, когда должна производиться выплата 6) ЧИСТНЗ – Возвращает чистую приведенную стоимость для денежных потоков, которые не обязательно являются периодическими. Если данная функция недоступна или возвращает ошибку #ИМЯ?, установите и загрузите надстройку «Пакет анализа». ЧИСТНЗ(ставка;значения;даты) где, Ставка — это ставка дисконтирования, применяемая к денежным потокам. Значения — это ряд денежных потоков, соответствующий графику платежей приведенной в аргументе даты. Первый платеж является необязательным и соответствует выплате в начале инвестиции. Если первое значение является выплатой, оно должно быть отрицательным. Все последующие выплаты дисконтируются на основе 365-дневного года. Ряд значений должен содержать по крайней мере одно положительное и одно отрицательное значения. Даты — это расписание дат платежей, которое соответствует ряду денежных потоков. Первая дата означает начальную величину в графике платежей. Все другие даты должны быть позже этой даты, но могут идти в произвольном порядке. ЗАДАЧИ 1) Пример использования функции ПС Предположим, Вы хотите к 01.01.16г. накопить 500 000 у.е.. Какую сумму нужно будет положить на счет в банке 01.01.текущего года., если в начале каждого месяца Вы будете выплачивать 2000 у.е.. Ставка банковского процента 3% годовых. 1. В созданном ранее файле Информационные системы, создайте таблицу, используя данные из рис. 1.
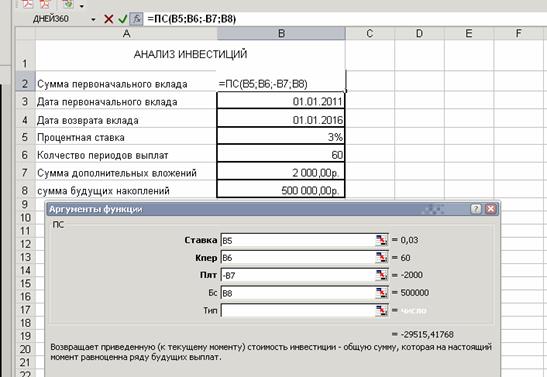
Рис. 1. Исходные данные для Задачи на функцию ПС 2. Вначале необходимо рассчитать КОЛИЧЕСТВО ПЕРИОДОВ ВЫПЛАТ, Нам потребуется функция ДНЕЙ(360). В ячейку В6 введите следующую формулу: =(ДНЕЙ360(B3;B4)*12)/360. 3. В ячейке В2 произвести расчет с помощью функции ПС. Откроется диалоговое окно мастера. Заполнить аргументы в соответствии с рис. 2.
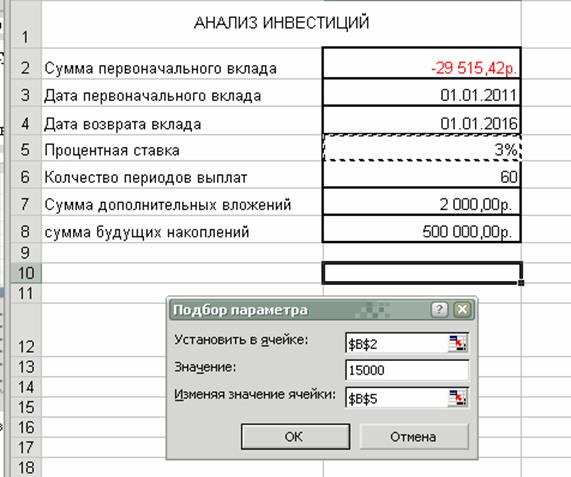
Рис. 2. Пример использования аргументов функции ПС 4. С помощью команды ПОДБОР ПАРАМЕТРА из меню СЕРВИС определим размер процентной ставки, при условии, что сумма первоначального вклада составляет 15 000 руб. Для этого активируйте ячейку В10. Выберите п.м. Сервис – подбор параметра и заполните в соответствии с рис. 3.
Рис. 3. Окно диалога Подбор параметра 5. Сравните полученный результат с данными на рис. 4
Рис. 4. Окно диалога Результат подбора параметра
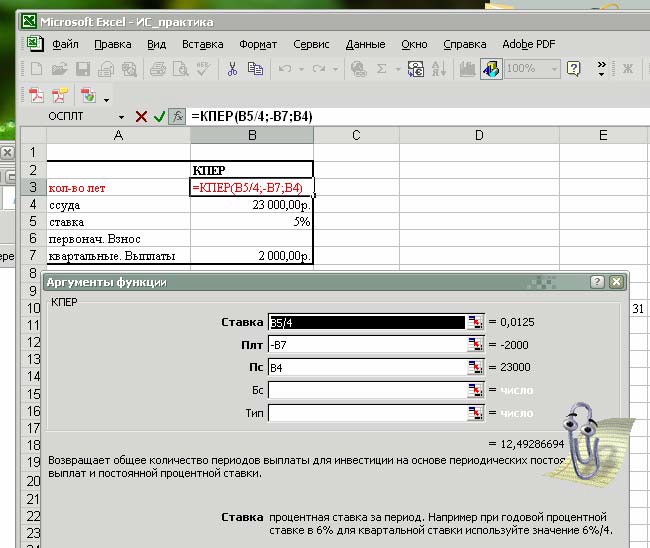
2) Пример использования функции КПЕР Вы берете в долг 23 000 руб. при годовой ставке 5%, и собираетесь выплачивать 2000 руб. ежеквартально. За какой период Вы погасите долг. Рассчитать задачу с помощью функции КПЕР. Пример решения задачи рис. 5.
Рис. 5. Пример использования аргументов функции КПЕР
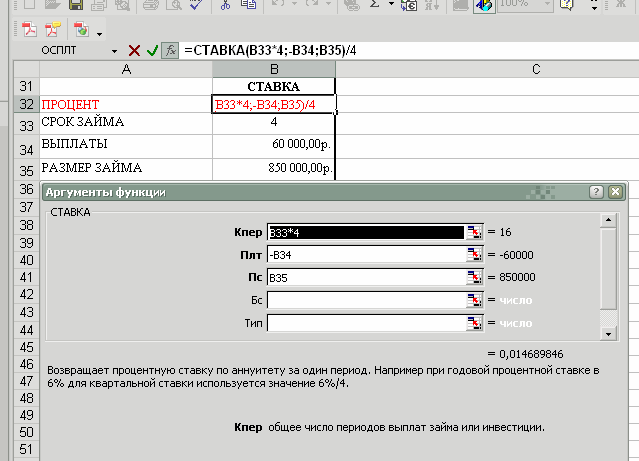
6) Пример использования функции СТАВКА Вы оформляете четырехлетний займ в размере 850 000 руб. с ежеквартальными выплатами 60 000 руб. Определить процентную ставку (пример решения задачи рис. 6)
Рис. 6. Пример использования аргументов функции СТАВКА
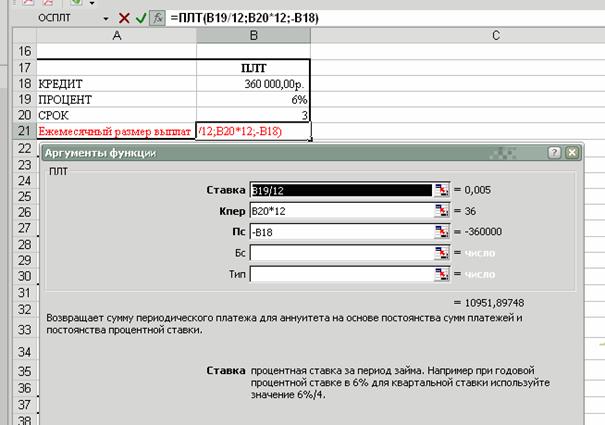
7) Пример использования функции ПЛТ Вы берете в долг 360 000 руб. сроком на 3 года, под 6% годовых, и обязуетесь погашать долг ежемесячно. Рассчитать ежемесячный размер выплат (пример решения задачи рис. 7)
Рис. 7. Пример использования аргументов функции ПЛТ
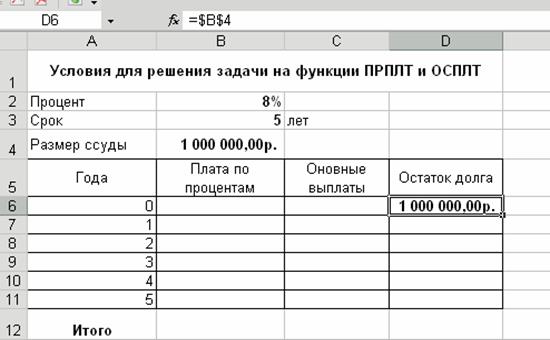
8) Пример использования функций ПРПЛТ и ОСПЛТ* Вы берете ипотечную суду размере 1 000 000 руб. под 8% годовых сроком на 5 лет. Рассчитайте плату по процентам, основные выплаты, остаток долга (по годам) и суммарные выплаты. 1. В созданном ранее файле Информационные системы на Лист2 создайте таблицу в соответствии с рис. 9.
Рис. 9. Условия для решения задачи с использованием финансовых функций ПРПЛТ и ОСПЛТ 2. В ячейку В7, с помощью мастера функций, добавьте следующее выражение: =ПРПЛТ($B$2;A7;$B$3;-$B$4). Скопируйте данную формулу до ячейки В11. 3. В ячейку С7, с помощью мастера функций добавьте следующую формулу: =ОСПЛТ($B$2;A7;$B$3;-$B$4). Скопируйте данную формулу до ячейки С11. 4. В ячейку D7 запишите формулу: =D6-C7. Скопируйте формулу до ячейки D11. Сравните полученный результат с данными на рис. 10. Решите следующую задачу: Вы берете ссуду 500000 руб. на срок 15 лет при годовой ставке 10 %. Рассчитайте основные платежи, плату по процентам, общую ежегодную плату и остаток долга.
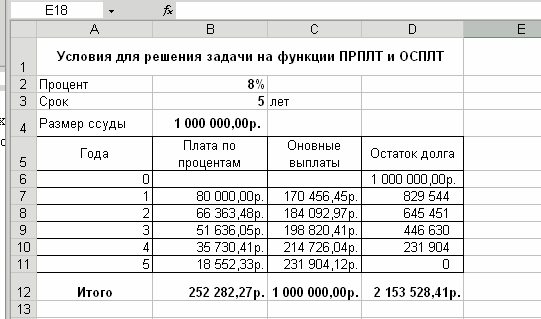
Рис. 10. Решение задачи с использованием финансовых функций ПРПЛТ и ОСПЛТ
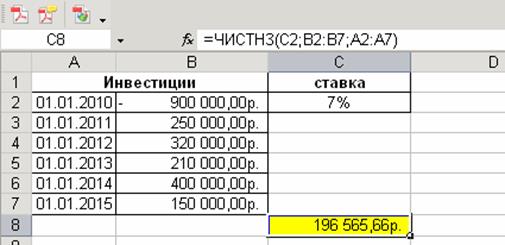
9) Пример расчета чистой текущей стоимости проекта с помощью функции ЧИСТНЗ Инвестиции в проект составляют 900 тыс. руб. В последующие 5 лет ожидаются следующие годовые доходы по проекту: 01.02.2010 – начальная инвестиция (900 тыс. руб.) 01.02.2011 – 250 тыс. руб. 01.02.2012 – 320 тыс. руб. 01.02.2013 – 210 тыс. руб. 01.02.2014 – 400 тыс. руб. 01.03.2015 – 150 тыс. руб. Рассчитать чистую текущую стоимость проекта (пример решения задачи приведен на рис. 11)
Рис. 11. Пример ввода аргументов функции ЧИСТНЗ
ЛАБОРАТОРНАЯ РАБОТА № 2 Финансовые функции для расчета амортизации (АПЛ, АСЧ, ФУО, ДДОБ) Амортизация (финансы) — структура выплат, связанная с погашением финансовых заимствований. Microsoft Excel, с помощью встроенных функций, позволяет автоматизировать вычислении, возникающие при составлении планов амортизации. 1. Технология работы: на конкретном примере рассматривается применение всех функция для вычисления амортизации. Отройте ранее созданный файл – Информационные системы, и Лист2 переименуйте в – Амортизация. Все задачи сохранять на данном листе ОПИСАНИЕ ФУНКЦИЙ: 1) АПЛ – возвращает величину амортизации актива за один период, рассчитанную линейным методом (под остаточной стоимостью подразумевается ликвидационная стоимость). АПЛ(нач_стоимость;ост_стоимость;время_эксплуатации), где, Нач_стоимость – затраты на приобретение актива; Ост_стоимость – стоимость в конце периода амортизации (иногда называется остаточной стоимостью актива); Время_эксплуатации – количество периодов, за которые актив амортизируется (иногда называется периодом амортизации). 2) АСЧ – возвращает величину амортизации актива за данный период, рассчитанную методом «суммы (годовых) чисел» (метод суммы чисел лет срока полезного использования – в бухгалтерском учете). АСЧ(нач_стоимость;ост_стоимость;время_эксплуатации;период) где, Нач_стоимость — затраты на приобретение актива; Ост_стоимость — стоимость в конце периода амортизации (иногда называется остаточной стоимостью актива); Время_эксплуатации — количество периодов, за которые актив амортизируется (иногда называется периодом амортизации); Период — период (должен быть измерен в тех же единицах, что и время полной амортизации). 3) ФУО – возвращает величину амортизации актива для заданного периода, рассчитанную методом фиксированного уменьшения остатка. ФУО(нач_стоимость;ост_стоимость;время_эксплуатации;период;месяцы) где, Нач_стоимость — это затраты на приобретение актива; Ост_стоимость — это стоимость в конце периода амортизации (иногда называется остаточной стоимостью актива); Время_эксплуатации — это количество периодов, за которые собственность амортизируется (иногда называется периодом амортизации); Период — это период, для которого требуется вычислить амортизацию. Период должен быть измерен в тех же единицах, что и время_эксплуатации; Месяцы — это количество месяцев в первом году. Если аргумент «месяцы» опущен, то предполагается, что он равен 12. 4) ДДОБ - возвращает значение амортизации актива за данный период, используя метод двукратного учета амортизации (метод уменьшающегося остатка – в бухгалтерском учете). ДДОБ(нач_стоимость;ост_стоимость;время_эксплуатации;период;коэффициент) где, Нач_стоимость — это затраты на приобретение актива.; Ост_стоимость — это стоимость в конце периода амортизации (иногда называется остаточной стоимостью актива); Время_эксплуатации — это количество периодов, за которые собственность амортизируется (иногда называется периодом амортизации); Период — это период, для которого требуется вычислить амортизацию. Период должен быть измерен в тех же единицах, что и время_эксплуатации; Коэффициент — процентная ставка снижающегося остатка. Если коэффициент опущен, то он полагается равным 2 (метод удвоенного процента со снижающегося остатка).
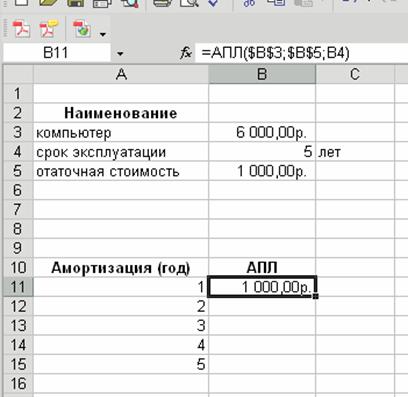
ЗАДАЧА Вы купили компьютер стоимостью 6000 руб. срок эксплуатации которого, составляет 5 лет, после чего он оценивается в 1000 руб. Рассчитайте: 1) снижение стоимости компьютера для каждого года эксплуатации (функция АПЛ). Пример решения задачи на рис. 1.
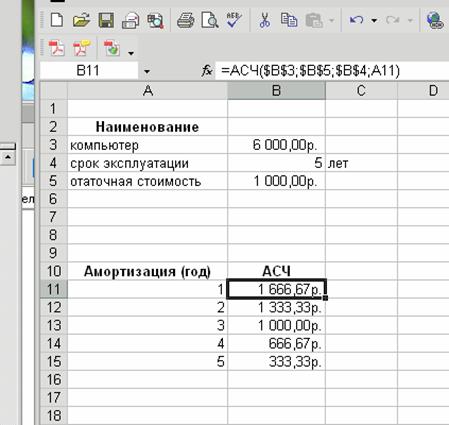
Рис. 1. Пример ввода аргументов функции АПЛ 2) амортизацию за первый и последний год эксплуатации компьютера (функция АСЧ). Пример решения задачи рис. 2.
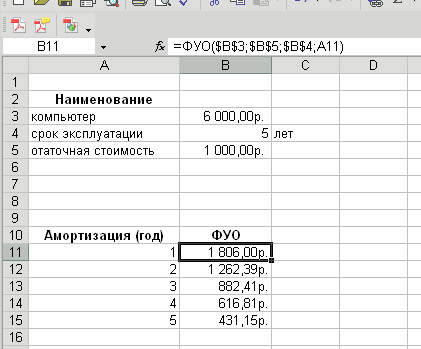
Рис. 2. Пример ввода аргументов функции АСЧ 3) амортизацию имущества за заданный период, используя метод постоянного учета амортизации (функция ФУО). Пример решения задачи рис. 3.
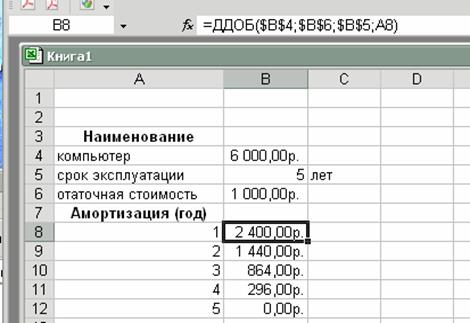
Рис. 3. Пример ввода аргументов функции ФУО 4) для каждого года эксплуатации с помощью функции ДДОБ (пример решения задачи приведен на рис. 4).
Рис. 4. Пример ввода аргументов функции ДДОБ Решите следующую задачу*: Вы купили за 24000 руб. компьютер, срок эксплуатации 5 лет, после чего оценивается в 9000 руб. Рассчитайте: 1) снижение стоимости компьютера для каждого года эксплуатации, 2) амортизацию за первый и второй года эксплуатации компьютера, 3) амортизацию имущества за весь период, используя метод постоянного учета амортизации
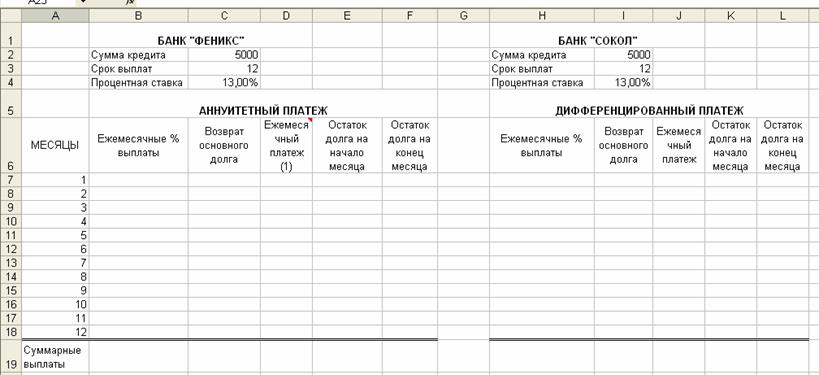
ЛАБОРАТОРНАЯ РАБОТА № 3 Финансовая математика на примере расчета стоимости банковского кредита Когда мы приносим в банк сбережения, мы продаем деньги, когда мы берем у банка кредит, мы покупаем деньги. Задача банка как продавца – преподнести свое кредитное предложение наиболее выигрышным способом. Наша задача как покупателей – выяснить истинную стоимость денег, которую предлагается заплатить. Excel с его мощным математическим аппаратом позволяет решать задачи подобного рода. Российские банки применяют в настоящий момент два способа погашения долга – аннуитетными (равными) и дифференцированными (уменьшающимися) платежами. На примере решения задачи, с помощью встроенных финансовых функций, мы сможем понять, как банки составляют график выплат по кредиту. ЗАДАЧА: Банк «ФЕНИКС» предлагает кредит в 5000 у.е. на 12 месяцев под 13% годовых. Выплаты кредита ежемесячно равными частями (аннуитет). Банк «СОКОЛ» предлагает аналогичные условия, но с дифференцированными выплатами. Дополнительные комиссии в обоих случаях не предусматриваются. Сколько заемщик заплатит банку «Феникс» и банку «Сокол»? РЕШЕНИЕ: 1. Откройте ранее созданный файл Информационные системы.xls, активируйте Лист3 и присвойте данному листу имя: Банковский кредит. 2. Создайте следующие таблицы (см. рис. 1).
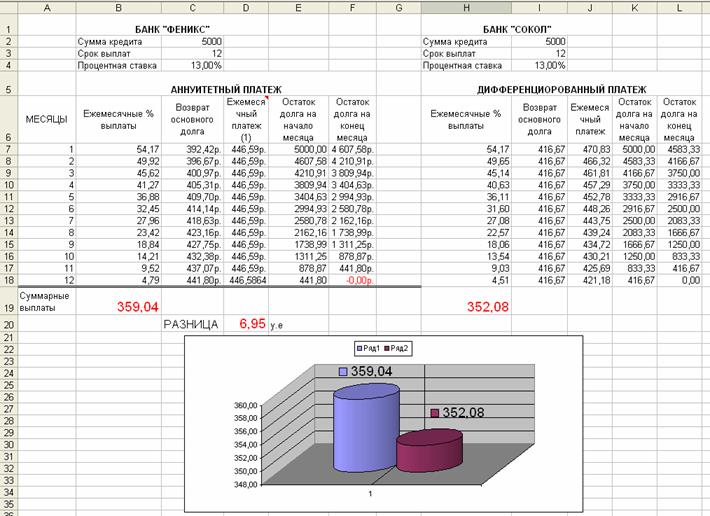
Рис. 1. Исходные данные для решения задачи Вначале произведем расчет по банку «Феникс», т.е. АННУИТЕТНЫЕ ВЫПЛАТЫ. 1. После Всех вычислений произведите расчет СУММАРНЫХ ВЫПЛАТ банка «СОКОЛ» по столбцу ЕЖЕМЕСЯЧНЫЕ % ВЫПЛАТЫ (с помощью функции СУММ()). Суммарные ежемесячные процентные выплаты по дифференцированному платежу составляют 352,08 у.е 2. Рассчитайте разницу между выплатами – она составит 6,95 у.е. 3. Постройте диаграмму (тип Цилиндрическая) в качестве цифровых значений выбрать СУММАРНЫЕ % ВЫПЛАТЫ.
4. Сохраните Вашу работу. Задачи для самостоятельного решения ЗАДАЧА 1. Банк А выдает ипотечный кредит в 2 000 000 на 10 лет под 14% годовых с комиссией за выдачу в 1,5% от суммы кредита и практикует дифференцированные выплаты. Банк Б – под 10% годовых берет фиксированную комиссию в 300 у.е. и практикует аннуитетные выплаты. Чье предложение выгоднее? ЗАДАЧА 2. Телевизор, стоимостью 40 тыс. руб. можно приобрести по программе «10/10/10» (10 месяцев, 10% первый взнос и удорожание товара на 10%). Дополнительные комиссии – 1% от ежемесячного платежа по кредиту (при переводе денег через почту в пользу банка-кредитора). Выгоднее ли взять обыкновенный кредит в банке на 10 месяцев под 16% годовых при условии дифференцированных выплат по кредиту. Дополнительная комиссия 2,5% от суммы кредита за его оформление. Погашение кредита – в отделении банка БЕЗ КОМИССИИ.
ЛАБОРАТОРНАЯ РАБОТА № 4 Задание на закрепление пройденного материала по использованию финансовых функций MS Excel 1. Решить задачи, используя финансовые функции Excel (рассмотренные в предыдущих лабораторных работах). 2. Исходные данные для задач № 1-5 находятся в табл. 1, (номер выбираемого варианта определяется ПО ПЕРВОЙ БУКВЕ ВАШЕЙ ФАМИЛИИ). 3. Решение задач производить в файле Информационные системы.xls на Лист4, которому присвоить имя – Самостоятельные работы. Исходные данные для решения задач смотри в таблице ниже. ЗАДАЧА 1 21.04.10 в банке был открыт на счет на сумму V1 тыс.р. денежных средств. Сколько денежных средств будет на счете 01.04.2016, если ставка банковского процента N1% годовых не меняется ЗАДАЧА 2 Какую денежную сумму необходимо вложить в банк 01.06.11, если к 01.01.2014 мы хотим получить V2 тыс. руб. Ставка банковского процента N2 % годовых и не меняется за все время хранения денег. ЗАДАЧА 3 15 марта 2011 г. в банке был открыт счет на сумму V3 тыс. руб. Какую сумму денег необходимо вносить дополнительно в начале каждого месяца, если к 01.05.2015 на счете необходимо иметь B3 тыс. руб. Ставка банковского процента не меняется за все время хранения вклада и составляет N3 % годовых. ЗАДАЧА 4 1 апреля 2010 г. в банке был открыт счет на сумму V4 тыс. руб. За какой период времени, на счете накопится B4 тыс. руб. Ставка банковского процента N4 % годовых ЗАДАЧА 5 Под какой процент (годовых) в банке можно открыть счет на сумму V5 тыс.руб., чтобы, через S5 лет получить В5 тыс. руб. Ответ оформить в соответствии с табл. 2. Исходные данные для решения задач № 1-5 Таблица 1
ЗАДАЧА 6 Вычислить n-годичную ипотечную ссуду покупки квартиры за P руб. с годовой ставкой i% и начальным взносом А% от стоимости квартиры (табл. 2). Рассчитайте основные платежи, ату по процентам общую ежегодную плату и остаток долга. Исходные данные для решения задачи № 6 Таблица 2
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||