Вариант определяется по последней цифре зачётной книжки следующим образом
|
Последняя цифра
|
Номер варианта
|
|
1
|
1
|
|
2
|
2
|
|
3
|
3
|
|
4
|
4
|
|
5
|
5
|
|
6
|
6
|
|
7
|
7
|
|
8
|
8
|
|
9
|
9
|
|
0
|
10
|
Решение задач должно быть обязательно выполнено в рукописном виде. Условие задачи переписывается полностью перед решением.
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ
Задание 1.
На испытание поставлено N0 однотипных устройств. За время t часов из строя вышло n(t ) штук устройств. За последующий интервал времени ∆t из строя вышло n(∆t ) устройств. Требуется вычислить вероятность безотказной работы за время t и t + ∆t , частоту отказов и интенсивность отказов на интервале ∆t .
Исходные данные для решения задачи приведены в таблице
|
Вариант
|
N0
|
t , час.
|
∆t , час.
|
n(t )
|
n(∆t )
|
|
1
|
1000
|
1000
|
100
|
245
|
15
|
|
2
|
1000
|
700
|
100
|
200
|
16
|
|
3
|
1000
|
2200
|
100
|
405
|
12
|
|
4
|
1000
|
1700
|
100
|
341
|
13
|
|
5
|
45
|
20
|
10
|
32
|
8
|
|
6
|
45
|
0
|
5
|
0
|
1
|
|
7
|
45
|
30
|
5
|
27
|
4
|
|
8
|
45
|
70
|
5
|
41
|
3
|
|
9
|
1000
|
7000
|
1000
|
250
|
40
|
|
10
|
1000
|
22000
|
1000
|
890
|
35
|
Задание 2.
В течение времени ∆t производилось наблюдение за восстанавливаемым устройством и было зафиксировано n(∆t ) отказов. До начала наблюдения устройство проработало t1 часов. Общее время наработки к концу наблюдения составило t2 часов. Требуется найти наработку на отказ.
Исходные данные для решения задачи приведены в таблице
|
Вариант
|
t1, час.
|
t2 , час.
|
n(∆t ) , час.
|
|
1
|
350
|
1280
|
15
|
|
2
|
400
|
1600
|
3
|
|
3
|
1000
|
6400
|
9
|
|
4
|
770
|
4800
|
7
|
|
5
|
1200
|
5558
|
2
|
|
6
|
300
|
540
|
12
|
|
7
|
540
|
1200
|
5
|
|
8
|
300
|
3200
|
8
|
|
9
|
12
|
184
|
16
|
|
10
|
570
|
2000
|
27
|
Задание 3.
Система из N устройств, имеющих разную надёжность. Известно, что каждый из приборов, проработав вне системы ti часов, имел ni отказов. Для каждого из устройств справедлив экспоненциальный закон надёжности. Требуется найти наработку на отказ всей системы.
Исходные данные для решения задачи приведены в таблице
|
Вариант
|
N
|
t1 , час.
|
n1
|
t2 , час.
|
n2
|
t3 , час.
|
n3
|
t4 , час.
|
n4
|
t5 , час.
|
n5
|
|
1
|
5
|
256
|
6
|
540
|
8
|
780
|
10
|
250
|
4
|
900
|
12
|
|
2
|
3
|
2000
|
6
|
1860
|
4
|
2160
|
3
|
–
|
–
|
–
|
–
|
|
3
|
4
|
960
|
12
|
1112
|
15
|
808
|
8
|
1490
|
7
|
–
|
–
|
|
4
|
5
|
90
|
3
|
270
|
6
|
140
|
4
|
230
|
5
|
180
|
3
|
|
5
|
5
|
600
|
45
|
600
|
2
|
200
|
4
|
200
|
6
|
200
|
2
|
|
6
|
3
|
144
|
6
|
125
|
5
|
80
|
3
|
–
|
–
|
–
|
–
|
|
7
|
4
|
720
|
3
|
1040
|
4
|
500
|
2
|
1800
|
6
|
–
|
–
|
|
8
|
3
|
1650
|
3
|
150
|
5
|
176
|
10
|
–
|
–
|
–
|
–
|
|
9
|
4
|
120
|
1
|
120
|
2
|
90
|
8
|
700
|
1
|
–
|
–
|
|
10
|
3
|
4800
|
9
|
5500
|
3
|
1200
|
3
|
–
|
–
|
–
|
–
|
Задание 4.
Устройство состоит из N элементов, средняя интенсивность отказов которых lср . Требуется вычислить вероятность безотказной работы в течение времени t и среднюю наработку до первого отказа.
Исходные данные для решения задачи приведены в таблице
|
Вариант
|
N
|
tср , час-1.
|
t , час.
|
|
1
|
20 500
|
2 × 10-5
|
2
|
|
2
|
1 000
|
0,5 × 10-3
|
0,5
|
|
3
|
2 000
|
5 × 10-6
|
10
|
|
4
|
95 000
|
0,5 × 10-6
|
2
|
|
5
|
150 000
|
0,25 × 10-6
|
4
|
|
6
|
45 000
|
0,5 × 10-5
|
2
|
|
7
|
300 000
|
0,2 ×10-7
|
8
|
|
8
|
50 000
|
0,2 × 10-6
|
5
|
|
9
|
170 000
|
0,7 × 10-6
|
3
|
|
10
|
189 000
|
1,4 × 10-6
|
2
|
Задание 5.
Устройство состоит из N элементов. Надёжность каждого элемента характеризуется вероятностью pi (t ) безотказной работы в течение времени t . Требуется найти вероятность безотказной работы устройства.
Исходные данные для решения задачи приведены в таблице
|
Вариант
|
N
|
p1(t )
|
p2 (t )
|
p3 (t )
|
p4 (t )
|
p5 (t )
|
p6 (t )
|
p7 (t )
|
p8 (t )
|
|
1
|
6
|
0,945
|
0.945
|
0,95
|
0,955
|
0,96
|
0,96
|
–
|
–
|
|
2
|
7
|
0,922
|
0,922
|
0,93
|
0.93
|
0,94
|
0,94
|
0,95
|
–
|
|
3
|
5
|
0,922
|
0,93
|
0,94
|
0,945
|
0,95
|
–
|
–
|
–
|
|
4
|
6
|
0,95
|
0,96
|
0,97
|
0,97
|
0,975
|
0,98
|
–
|
–
|
|
5
|
7
|
0,98
|
0,98
|
0,982
|
0,982
|
0,984
|
0,984
|
0,98
|
–
|
|
6
|
8
|
0,984
|
0,984
|
0,986
|
0,986
|
0,988
|
0,988
|
0,99
|
0,99
|
|
7
|
5
|
0,992
|
0,994
|
0,996
|
0,998
|
0,999
|
–
|
–
|
–
|
|
8
|
6
|
0,922
|
0,93
|
0,94
|
0,945
|
0,948
|
0,949
|
–
|
–
|
|
9
|
5
|
0,95
|
0,955
|
0,96
|
0,965
|
0,97
|
–
|
–
|
–
|
|
10
|
8
|
0,9998
|
0,9998
|
0,9996
|
0,9996
|
0,9994
|
0,9994
|
0,9992
|
0,9992
|
Задание 6.
В системе могут быть использованы только те элементы, средняя интенсивность отказов которых равна lср . Система состоит из N элементов. Требуется определить среднюю наработку до первого отказа и вероятность безотказной работы в конце первого часа.
Исходные данные для решения задачи приведены в таблице
|
Вариант
|
lср , час-1.
|
N
|
|
1
|
3,5 × 10-5
|
200
|
|
2
|
2 × 10-6
|
700
|
|
3
|
2 × 10-5
|
10 000
|
|
4
|
2 × 10-6
|
50 000
|
|
5
|
4 ×10-4
|
500
|
|
6
|
2 × 10-6
|
2 500
|
|
7
|
2 ×10-7
|
8 000
|
|
8
|
1× 10-5
|
50
|
|
9
|
4 × 10-6
|
60
|
|
10
|
2,5 × 10-3
|
20
|
Задание 7.
Известны интенсивность отказов конденсатора λ, интенсивность отказов конденсатора по обрыву и замыканию (пробою) λ0 , λ3 = λ1.
Вероятность того, что отказ конденсатора произойдёт из-за обрыва, описывается формулой 𝜑0 = λ0 / (λ0 +λ1). Задано время непрерывной работы схемы t . Предполагается, что последействие отказов отсутствует. Найти вероятность безотказной работы схем соединения конденсаторов, представленных в таблице
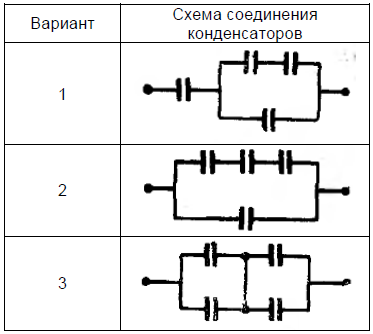
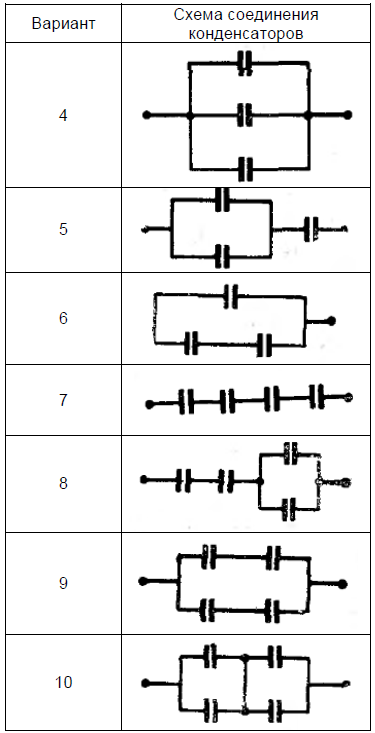
Задание 8.
В результате исследования пульта контроля с высокой плотностью информации осуществляется контроль комплекса параметров путём считывания показателей со шкал пульта. При считывании стократно фиксировалась длительность операции контроля в секундах. Требуется на основании полученного вариационного ряда длительности операций контроля выяснить соответствие полученных данных определённым законам распределения.
Исходные данные для решения задачи приведены в таблице. Если у значения не указана частота, значит оно появлялось один раз.
|
Вар
|
Значение (частота)
|
|
1
|
1 (2)
|
1,8
|
2,1
|
2,2 (3)
|
2,3
|
2,4
|
2,5
|
2,6
|
2,8 (6)
|
3 (2)
|
|
3,2 (4)
|
3,4 (4)
|
3,6 (2)
|
3,7
|
4 (3)
|
4,1
|
4,2 (3)
|
4,4 (3)
|
4,6 (4)
|
4,7
|
|
4,8 (2)
|
5 (6)
|
5,2 (4)
|
5,4 (3)
|
5,5 (3)
|
5,6 (2)
|
5,7 (2)
|
5,8 (5)
|
6 (2)
|
6,1 (2)
|
|
6,2 (2)
|
6,6
|
6,8
|
7 (2)
|
7,2 (2)
|
7,4
|
7,8
|
7,9
|
8
|
8,1
|
|
8,7
|
8,8
|
10,8
|
11
|
11,4
|
11,8
|
12
|
13,2
|
13,4
|
14,1
|
|
18,8
|
|
|
|
|
|
|
|
|
|
|
2
|
4,6
|
7,8 (2)
|
9,7 (2)
|
10,4 (4)
|
11,2
|
11,4 (3)
|
11,5 (3)
|
11,8
|
12 (3)
|
12,6 (5)
|
|
13,2
|
13,6 (2)
|
13,8 (2)
|
14 (3)
|
14,2 (4)
|
14,7 (3)
|
15,6 (3)
|
16,2 (2)
|
16,4 (5)
|
16,8 (4)
|
|
17,9 (3)
|
18,4 (3)
|
18,9 (3)
|
19,4 (2)
|
19,6 (4)
|
19.9 (3)
|
20,6 (3)
|
21,3 (4)
|
22,4 (2)
|
23,5 (3)
|
|
24,2 (2)
|
25,5(2)
|
26,3 (4)
|
27,2 (4)
|
30,2
|
31,8
|
35,6
|
39
|
|
|
|
3
|
4,7 (2)
|
6,4
|
7,3 (3)
|
8,4 (2)
|
9,6 (2)
|
10 (2)
|
10,4 (2)
|
10,7 (3)
|
11,2 (7)
|
11,8 (2)
|
|
12 (4)
|
12,3 (3)
|
13 (5)
|
13,6 (6)
|
14,2 (5)
|
14,8 (2)
|
15,6 (8)
|
16,5 (2)
|
17,4 (5)
|
18 (3)
|
|
18,4 (3)
|
19 (3)
|
20,2 (3)
|
20,7 (2)
|
22,5 (2)
|
23,4 (2)
|
24,6 (2)
|
25 (3)
|
25,8
|
26,4
|
|
28,3
|
29,6
|
31,9
|
32,6
|
34
|
37
|
37,9
|
42,6
|
52,6
|
|
|
4
|
1,9 (4)
|
3,4 (3)
|
4,3 (5)
|
4,8 (4)
|
5,5 (7)
|
6,2 (4)
|
6,7 (4)
|
7,2 (7)
|
7,8 (8)
|
8,2 (4)
|
|
8,6 (4)
|
9,5 (8)
|
10,5 (3)
|
11,5 (5)
|
12 (4)
|
12,2 (4)
|
13,4 (3)
|
14,7
|
15,5 (2)
|
16,2
|
|
17,6
|
18,5 (3)
|
20,1
|
22,2
|
24
|
26,4 (2)
|
27,2 (2)
|
31,6
|
36
|
45,3
|
|
57
|
|
|
|
|
|
|
|
|
|
|
5
|
6,6
|
8
|
10,7 (2)
|
11,3 (3)
|
12,4 (4)
|
13,2 (3)
|
13,8 (2)
|
14,3 (6)
|
15 (3)
|
15,8 (3)
|
|
16 (4)
|
16,3 (4)
|
16,8 (2)
|
17,7 (3)
|
18,6 (4)
|
18,8 (2)
|
19 (2)
|
19,4 (3)
|
19,8 (3)
|
20,4 (5)
|
|
21,2 (4)
|
21,8 (3)
|
22,2 (3)
|
22,4 (4)
|
22,8
|
23,6
|
24,4
|
24,6 (2)
|
26,3 (3)
|
27,5 (2)
|
|
28,7
|
29,3 (2)
|
30,2 (2)
|
31,6
|
35,2
|
36,4
|
41,8
|
42
|
45,4
|
49,4
|
|
53,2
|
54
|
60,8
|
79,2
|
|
|
|
|
|
|
|
6
|
1,8
|
2,2 (2)
|
2,7 (2)
|
3,2
|
3,8 (3)
|
4,2 (6)
|
4,7 (2)
|
5,6 (4)
|
6 (2)
|
6,3 (6)
|
|
6,8 (3)
|
7 (3)
|
7,4 (6)
|
7,7 (4)
|
8,1 (4)
|
8,2 (7)
|
8,3 (3)
|
9,3 (4)
|
9,8 (4)
|
10,3 (3)
|
|
10,8 (2)
|
11,6
|
12,4 (4)
|
13,4 (3)
|
14,4 (3)
|
15,4 (2)
|
16,5 (3)
|
17,4 (2)
|
19,4 (2)
|
20,8 (2)
|
|
22,4
|
23,6 (2)
|
24,6
|
27
|
32,4
|
|
|
|
|
|
|
7
|
2,5
|
3,7
|
4,8 (2)
|
5,6
|
6,7
|
7,1 (3)
|
8,3 (4)
|
8,7 (4)
|
9,2 (5)
|
10 (4)
|
|
10,4 (7)
|
10,8 (6)
|
11,4 (9)
|
11,8 (4)
|
12,1 (4)
|
12,6 (7)
|
13,4 (3)
|
14,1 (7)
|
14,6 (5)
|
15,4 (4)
|
|
16,1 (3)
|
17,4 (2)
|
18,4
|
19
|
19,4 (3)
|
19,8
|
21
|
25,2
|
26
|
30,2
|
|
31,8
|
40,4
|
51,6
|
|
|
|
|
|
|
|
|
8
|
4,9
|
5,8
|
6
|
6,2
|
7,7
|
8,9
|
9,4
|
10,2
|
12,4
|
12,6
|
|
12,7
|
13
|
14,4
|
15,2
|
15,4
|
16 (3)
|
16,8 (2)
|
17,2 (2)
|
17,4
|
18,2 (2)
|
|
18,4
|
18,6 (2)
|
19,8
|
20 (2)
|
20,8
|
22,2 (3)
|
22,6 (2)
|
23,2
|
23,4
|
23,6
|
|
24,6 (2)
|
25 (2)
|
25,6
|
26
|
26,6
|
29
|
30,3
|
31,2
|
31,8
|
33
|
|
33,2
|
33,6
|
33,8 (2)
|
34,7 (3)
|
38,6 (5)
|
40,2 (2)
|
42,4
|
43,5 (3)
|
44,9
|
47,2 (5)
|
|
49,6 (2)
|
50,8
|
52,5 (2)
|
53,8 (2)
|
57,6 (2)
|
61,3 (3)
|
64,7 (4)
|
70,2 (2)
|
73,1 (2)
|
74,2
|
|
76,2
|
85,1
|
|
|
|
|
|
|
|
|
|
9
|
0,6 (3)
|
1,5 (6)
|
2,3 (9)
|
3,1 (4)
|
3,5 (10)
|
3,8 (5)
|
4,1 (8)
|
4,2 (6)
|
4,6 (9)
|
5,4 (9)
|
|
6,5 (7)
|
7,2 (6)
|
7,7 (4)
|
8,8 (2)
|
9,1 (2)
|
10,3 (2)
|
11,8
|
12,6
|
14,4
|
15,4 (2)
|
|
16,2
|
22,6
|
37
|
|
|
|
|
|
|
|
|
10
|
0,5 (2)
|
1,2 (3)
|
1,8 (4)
|
2,3 (3)
|
2,6 (3)
|
3,2 (6)
|
4,1 (6)
|
4,5 (9)
|
4,9 (3)
|
5,4 (5)
|
|
5,7 (2)
|
6,2 (10)
|
6,8 (7)
|
7,6 (9)
|
8 (3)
|
8,6 (3)
|
9,1 (3)
|
9,9 (2)
|
11,1 (2)
|
11,7 (2)
|
|
12,3 (4)
|
13,1 (2)
|
14,4 (2)
|
15,6
|
16,5 (2)
|
21
|
24,4
|
|
|
|
|


