КГСХА, техническая механика (расчетно-графическая работа)

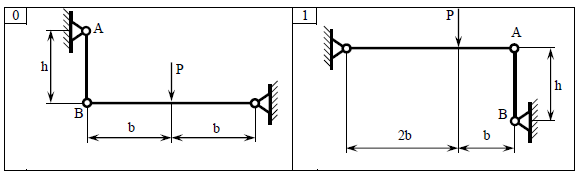
ЗАДАЧА № 1 РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ

Для заданной шарнирно-стержневой системы (таблица 1, рисунок 1) требуется:

1 Проверить прочность растянутого (сжатого) стержня АВ (материал – сталь Ст 3) указанного поперечного сечения по нормальным напряжениям, если [s]=160 МПа.

2 Подобрать сечение стержня АВ (материал – сталь Ст 3) в виде равнополочного уголка из условия наименьшего расхода материала, если [s]=160 МПа. Вычислить коэффициент запаса прочности по отношению к пределу текучести, если sТ = 240 МПа.

3 Определить удлинение (укорочение) подобранного растянутого (сжатого) стержня АВ, если Е = 2×10⁵ МПа.

Таблица 1 - Исходные данные

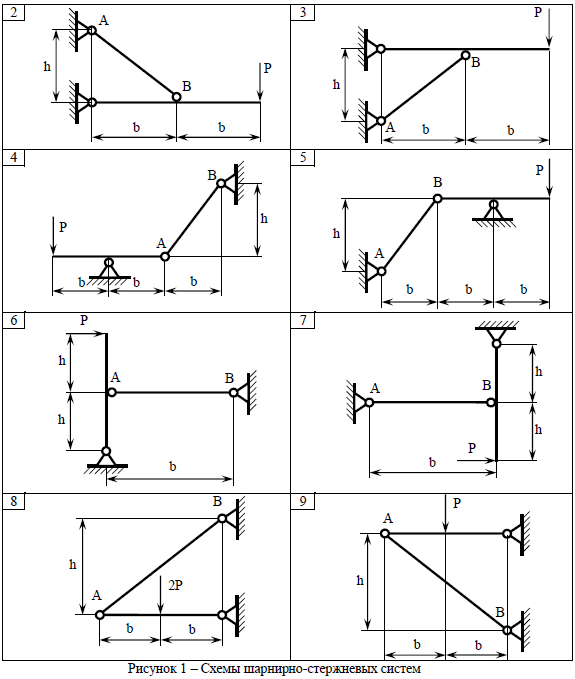
ЗАДАЧА № 2 ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙ БРУСЬЕВ

Для заданного поперечного сечения, элементы которого вплотную приставлены друг к другу (таблица 2, рисунок 4), требуется:

1 Вычертить сечение в масштабе 1:1 на листе формата А4 и показать основные размеры.

2 Определить положение центра тяжести.

3 Определить положение главных осей инерции.

4 Вычислить главные моменты инерции.

5 Показать на чертеже положение центра тяжести, главных осей инерции и все расстояния, полученные расчетным путем.

Таблица 2 – Исходные данные

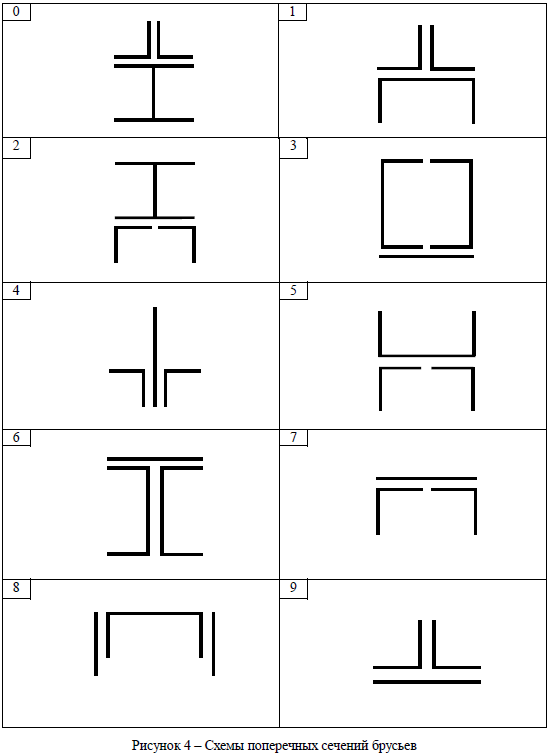
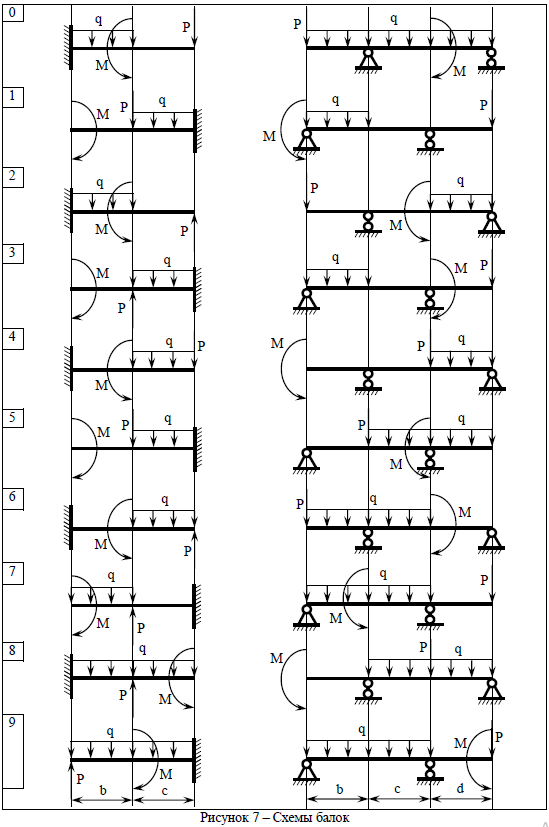
ЗАДАЧА № 3 ПРЯМОЙ ПОПЕРЕЧНЫЙ ИЗГИБ БАЛОК

Для заданных балок (таблица 3, рисунок 7) требуется:

1 Построить эпюры внутренних усилий с вычислением значений поперечных сил и изгибающих моментов в характерных сечениях балок.

2 Проверить прочность консольной балки (материал – сталь Ст 3) заданного поперечного сечения по нормальным напряжениям, если [s]=160 МПа.

3 Для двухопорной балки (материал – сталь Ст 3) подобрать поперечное сечение в форме двутавра из условия прочности по нормальным напряжениям, если [s]=160 МПа. Вычислить коэффициент запаса прочности по отношению к пределу текучести, если sт=240 МПа. Построить пространственную эпюру нормальных напряжений в опасном сечении балки.

Таблица 3 – Исходные данные

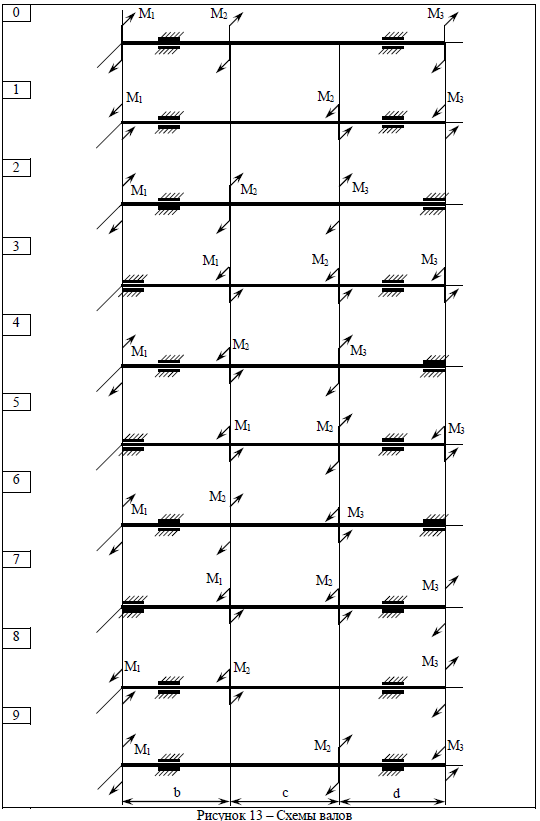
ЗАДАЧА № 4 КРУЧЕНИЕ ВАЛОВ КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ

Для заданного вала (таблица 4, рисунок 13) требуется:

1 Из условия равновесия определить направление и величину незаданного скручивающего момента.

2 Построить эпюру крутящих моментов.

3 Определить диаметр вала (материал – сталь Ст 5) на каждом участке из условия прочности по касательным напряжениям, если [t] = 90 МПа. Вычисленные диаметры округлить до ближайших больших целых значений.

4 Построить эпюру углов закручивания (углов поворота) поперечных сечений вала, приняв за неподвижное левое торцовое сечение, если G = 8×10⁴ МПа.

Примечание. Для участков вала, на которых крутящий момент равен нулю, диаметр вала принять равным наименьшему из диаметров на других участках.

Таблица 4 – Исходные данные

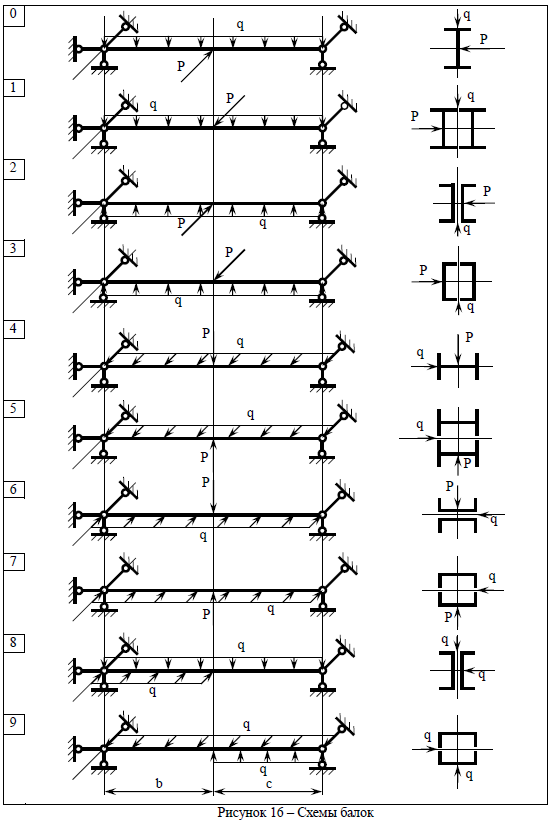
ЗАДАЧА № 5 КОСОЙ ИЗГИБ БАЛОК

Для заданной балки (таблица 5, рисунок 16) требуется:

1 Построить эпюры изгибающих моментов в главных плоскостях инерции.

2 Проверить прочность балки (материал – сталь Ст3) заданного сечения по нормальным напряжениям, если [s] = 160 МПа.

3 Построить пространственную эпюру нормальных напряжений и найти положение нейтральной линии в опасном сечении балки.

Таблица 5 – Исходные данные

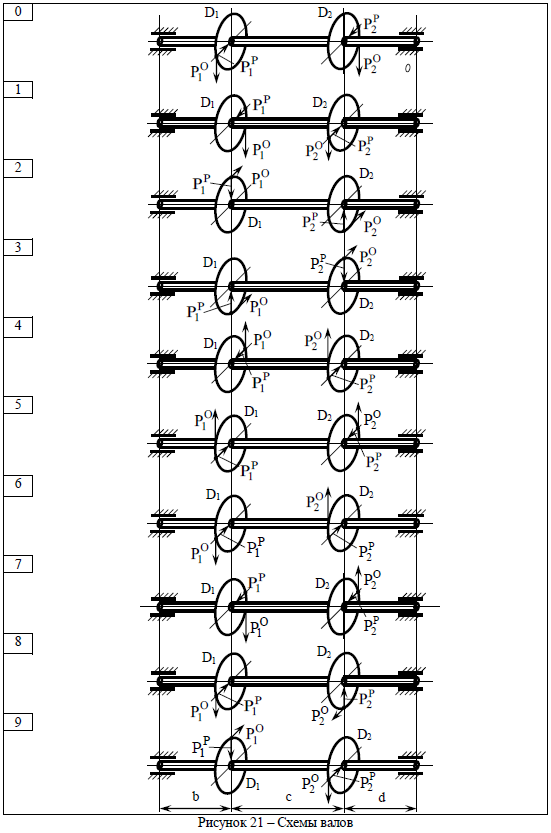
ЗАДАЧА № 6 ИЗГИБ С КРУЧЕНИЕМ ВАЛОВ КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ

Для заданного вала (таблица 6, рисунок 21) требуется:

1 Построить эпюры изгибающих моментов в вертикальной и горизонтальной плоскостях и эпюру крутящих моментов.

2 Определить диаметр вала (материал – сталь 45) в опасном сечении по третьей теории прочности, если [s] = 150 МПа. Вычисленный диаметр округлить до ближайшего большего целого значения.

Примечание. На рассчитываемый вал редуктора установлены прямозубые колеса. В точке зацепления возникают окружное P^O и радиальное P^Р усилия. Считать P^Р = 0,36 P^O.

Таблица 6 – Исходные данные

ЗАДАЧА № 7 ПЕРЕМЕЩЕНИЯ ПРИ ИЗГИБЕ БАЛОК

Для двухопорной балки (таблица 3, рисунок 7), рассчитанной в задаче № 3, требуется определить методом Мора прогиб и угол поворота торцового поперечного сечения консольного участка балки, если E = 2∙10⁵ МПа.