Вариант выполнения задачи определяется двумя последними цифрами номера зачетной книжки.
Описание решения задачи рекомендуется в следующей последовательности:
- условие задачи с исходными данными;
- подробное изложение алгоритма решения с цифровыми данными и графическими иллюстрациями; выводы.
Задача 1.
Обосновать выбор, описать метрологические характеристики и приемы применения средств измерений линейных размеров для заданных: номинального значения и допусков отверстия и вала, указанных в табл. 1.
Сформировать условное обозначение, определить вид и систему образования посадки, построить схему посадки отверстия и вала и рассчитать основные характеристики посадки, предельно допустимые размеры и допуски сопрягаемых деталей.
Таблица 1. Исходные данные для измерений.
|
Цифра номера зачетной книжки
|
9
|
8
|
7
|
6
|
5
|
4
|
3
|
2
|
1
|
0
|
|
Номинальный размер, мм
|
120
|
30
|
50
|
80
|
18
|
180
|
250
|
315
|
400
|
500
|
|
Номер квалитета отверстия
|
10
|
7
|
8
|
9
|
6
|
11
|
12
|
7
|
8
|
9
|
|
Номер квалитета вала
|
9
|
7
|
10
|
7
|
6
|
7
|
10
|
12
|
8
|
7
|
|
Основное отклонение отверстия
|
R
|
M
|
N
|
P
|
H
|
Js
|
H
|
F
|
G
|
K
|
|
Основное отклонение вала
|
u
|
f
|
h
|
k
|
d
|
e
|
g
|
m
|
r
|
s
|
Выбор задания: по двум последним цифрам номера зачетной книжки – по последней цифре – номинальный размер, номер квалитета вала и основное отклонение отверстия; по предпоследней цифре – номер квалитета отверстия и основное отклонение вала.
Задача 2.
Произведены прямые многократные измерения линейного размера. Результаты измерений представлены в виде отклонений от номинального значения. Экспериментальные значения распределены по интервалам, как приведено в табл. 2. Количество экспериментальных данных, попадающих в i-тый интервал, приведено в табл. 3.
Таблица 2. Распределение результатов измерений по интервалам значений
|
Номер интервала
|
Последняя цифра номера зачетной книжки
|
|
9
|
8
|
7
|
6
|
5
|
4
|
3
|
2
|
1
|
0
|
|
Интервалы отклонений от номинального значения, мкм
|
|
1
|
-5; -4
|
0; 2
|
-25; -20
|
-50; -40
|
0; 5
|
-2,5;-2
|
-100;-80
|
-500;-400
|
0; 4
|
-10;-8
|
|
2
|
-4; -3
|
2; 4
|
-20; -15
|
-40; -30
|
5; 10
|
-2;-1,5
|
-80; -60
|
-400;-300
|
4; 8
|
-8; -6
|
|
3
|
-3; -2
|
4; 6
|
-15; -10
|
-30; -20
|
10;15
|
-1,5;-1
|
-60; -40
|
-300;-200
|
8; 12
|
-6; -4
|
|
4
|
-2; -1
|
6; 8
|
-10; -5
|
-20; -10
|
15;20
|
-1;-0,5
|
-40; -20
|
-200;-100
|
12;16
|
-4; -2
|
|
5
|
-1; 0
|
8; 10
|
-5; 0
|
-10; 0
|
20;25
|
-0,5; 0
|
-20; 0
|
-100; 0
|
16;20
|
-2; 0
|
|
6
|
0; 1
|
10; 12
|
0; 5
|
0; 10
|
25;30
|
0; 0,5
|
0; 20
|
0; 100
|
20;24
|
0; 2
|
|
7
|
1; 2
|
12; 14
|
5; 10
|
10; 20
|
30;35
|
0,5; 1
|
20; 40
|
100;200
|
24;28
|
2; 4
|
|
8
|
2; 3
|
14; 16
|
10; 15
|
20; 30
|
35;40
|
1; 1,5
|
40; 60
|
200;300
|
28;32
|
4; 6
|
|
9
|
3; 4
|
16; 18
|
15; 20
|
30; 40
|
40;45
|
1,5; 2
|
60; 80
|
300;400
|
32;36
|
6; 8
|
|
10
|
4; 5
|
18; 20
|
20; 25
|
40; 50
|
45;50
|
2; 2,5
|
80; 100
|
400; 500
|
36;40
|
8; 10
|
|
Доверительная вероятность Р
|
0,95
|
0,975
|
0,98
|
0,99
|
0,90
|
0,80
|
0,995
|
0,98
|
0,95
|
0,99
|
Таблица 3. Распределение абсолютных частот по интервалам
|
Предпоследняя цифра номера зачетной книжки
|
Число экспериментальных данных, попадающих в i-тый интервал
|
|
Номер интервала
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
0
|
1
|
5
|
12
|
20
|
32
|
16
|
8
|
3
|
2
|
1
|
|
1
|
2
|
4
|
7
|
18
|
25
|
17
|
12
|
8
|
5
|
2
|
|
2
|
0
|
3
|
10
|
15
|
30
|
18
|
10
|
8
|
5
|
1
|
|
3
|
3
|
10
|
15
|
28
|
20
|
11
|
7
|
3
|
2
|
1
|
|
4
|
2
|
7
|
14
|
22
|
30
|
10
|
8
|
4
|
3
|
0
|
|
5
|
1
|
6
|
12
|
15
|
23
|
20
|
12
|
6
|
4
|
1
|
|
6
|
3
|
8
|
14
|
20
|
32
|
14
|
5
|
3
|
1
|
0
|
|
7
|
0
|
5
|
9
|
16
|
37
|
20
|
12
|
4
|
3
|
1
|
|
8
|
2
|
5
|
12
|
17
|
31
|
14
|
10
|
5
|
2
|
2
|
|
9
|
1
|
3
|
7
|
21
|
32
|
20
|
14
|
8
|
4
|
2
|
Требуется:
1. Построить гистограмму эмпирического распределения.
2. Проверить критерием Шарлье наличие и исключить имеющиеся промахи.
3. Проверить гипотезу о соответствии эмпирического распределения нормальному закону Гаусса с помощью критерия Пирсона χ2.
4. Построить доверительный интервал для результата многократных измерений.
Задача 3.
Произведены многократные измерения двух параметров а1 и а2. Известна функциональная зависимость (табл. 4) для определения косвенно измеряемой величины. Значения параметров а1 и а2 приведены в таблице. 5.
Таблица 4. Функциональная зависимость для косвенных измерений
|
|
Предпоследняя цифра номера зачетной книжки
|
|
9
|
8
|
7
|
6
|
5
|
4
|
3
|
2
|
1
|
0
|
|
Измеряемая величина
|
Площадь
|
Сила тока
|
Объем
|
Электри-
ческое
сопротив-
ление
|
Электри-
ческая
мощность
|
Сила тока
|
Плотность
|
Электри-
ческое
сопротив-
ление
|
Электри-
ческая
мощность
|
Напряжение
электрического
поля
|
|
Функциональная зависимость
|
S=a×b
|
I=U/R
|
V=a2×b
|
R=P/I2
|
I
|
P=U2/R
|
r=m/V
|
R=U/I
|
P=I2×R
|
U=P/I
|
|
Доверительная вероятность Р
|
0,9
|
0,95
|
0,975
|
0,98
|
0,99
|
0,995
|
0,997
|
0,998
|
0,95
|
0,98
|
Примечание: в функциональных зависимостях параметр «а1» стоит на первом месте в произведении либо в числителе дроби.
Таблица 5. Результаты многократных измерений аргументов
|
Последняя цифра номера зачетной книжки
|
Параметры
|
Значения измеряемых параметров (размерности – в единицах системы SI)
|
|
0
|
a1
|
12,2
|
11,8
|
12,1
|
12,4
|
11,9
|
12,5
|
11,3
|
13,0
|
12,9
|
12,3
|
|
a2
|
5,2
|
5,0
|
5,5
|
5,8
|
4,8
|
5,3
|
5,4
|
5,7
|
5,6
|
5,1
|
|
1
|
a1
|
8,1
|
8,3
|
8,7
|
7,8
|
7,9
|
8,2
|
8,6
|
8.8
|
8,0
|
8,5
|
|
a2
|
15,5
|
15,2
|
15,8
|
15,1
|
15,3
|
15,5
|
15,7
|
15,5
|
15,4
|
14,8
|
|
2
|
a1
|
3,8
|
3,3
|
3,5
|
2,9
|
2,8
|
3,6
|
3,4
|
2,9
|
3,0
|
3,2
|
|
a2
|
18,2
|
17,9
|
17,5
|
17,7
|
18,1
|
18,3
|
18,5
|
17,8
|
17,5
|
17,7
|
|
3
|
a1
|
20,2
|
20,1
|
20,4
|
20,2
|
19,8
|
19,7
|
20,5
|
20,1
|
19,5
|
19.9
|
|
a2
|
7,6
|
7,5
|
7,7
|
7,9
|
6,9
|
7,1
|
7,2
|
6,8
|
6,5
|
7,3
|
|
4
|
a1
|
10,4
|
10,1
|
9,9
|
9,7
|
10,3
|
10,0
|
9,5
|
9,8
|
10,4
|
10,5
|
|
a2
|
31,9
|
32,0
|
32,3
|
31,8
|
31,9
|
32,5
|
32,2
|
31,6
|
31,7
|
32,3
|
|
5
|
a1
|
50,2
|
50,5
|
50,0
|
49,8
|
49,9
|
50,1
|
49,4
|
49,7
|
50,0
|
50,2
|
|
a2
|
25,5
|
26,0
|
25,9
|
25,8
|
25,4
|
26,2
|
26,7
|
26,5
|
26,1
|
26,4
|
|
6
|
a1
|
3,2
|
3,3
|
2,9
|
2,8
|
3,1
|
3,0
|
2,7
|
2,5
|
2,2
|
3,8
|
|
a2
|
7,7
|
6,9
|
6,8
|
7,0
|
7,1
|
7,3
|
7,5
|
7,0
|
6,5
|
6,7
|
|
7
|
a1
|
4,3
|
4,0
|
3,8
|
3,9
|
3,5
|
4,1
|
4,5
|
3,7
|
3,8
|
4,6
|
|
a2
|
2,4
|
2,1
|
1,9
|
2,2
|
2,5
|
1,7
|
1,9
|
1,5
|
2,8
|
2,5
|
|
8
|
a1
|
8,9
|
8,8
|
9,5
|
9,2
|
8,5
|
8,7
|
8,9
|
9,3
|
9,1
|
9,2
|
|
a2
|
16,2
|
16,5
|
16,0
|
16,4
|
15,7
|
15,9
|
15,8
|
16,0
|
16,3
|
15,5
|
|
9
|
a1
|
28,9
|
29,0
|
29,2
|
28,7
|
28,6
|
29,1
|
29,4
|
29,2
|
28,7
|
28,9
|
|
a2
|
12,7
|
12,9
|
13,5
|
13,2
|
13,1
|
13,7
|
12,6
|
12,9
|
12,5
|
13,0
|
Требуется. Найти измеряемую косвенно с помощью функциональной зависимости величину и представить результат измерений в форме доверительного интервала с заданной доверительной вероятностью Р.
Задача 4.
Определите, какое средство измерений предпочтительно применять для обеспечения большей точности результатов.
Укажите пределы, в которых может находиться значение измеряемой величины при известных метрологических характеристиках применяемых средств измерений, приведенных в табл. 6 и 7.
Выразите размерность измеряемой величины через размерности основных величин системы SI.
Таблица 6. Характеристики средств измерений и измеряемых величин.
|
Предпоследняя
цифра номера
зачетной
книжки
|
9
|
8
|
7
|
6
|
5
|
4
|
3
|
2
|
1
|
0
|
|
Измеряемое
значение
|
400 мм3
|
350 Гн
|
80 мВ
|
280 кОм
|
70 мкФ
|
60°С
|
160 км/ч
|
450 кН
|
900 кВт
|
450 кПа
|
|
Диапазон
измерений
средства
измерений
|
№1
|
0 – 800 мм3
|
0 – 500 Гн
|
0 – 100 мВ
|
50 – 300 кОм
|
0 – 100 мкФ
|
50 – 200 °С
|
20 – 250 км/ч
|
0 – 1000 кН
|
100 – 2000 кВт
|
200 – 2000 кПа
|
|
№2
|
0 – 1000 мм3
|
100 – 1000 Гн
|
20 – 180 мВ
|
0 – 500 кОм
|
0 – 500 мкФ
|
0 – 500 °С
|
0 – 200 км/ч
|
100 – 500 кН
|
500 – 1000 кВт
|
100 – 500 кПа
|
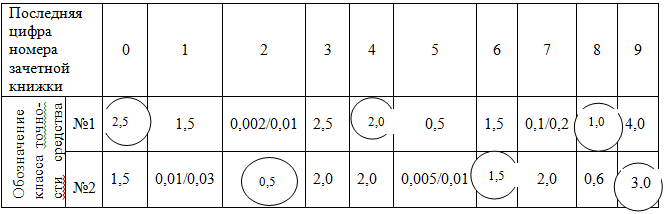
Таблица 7. Классы точности применяемых средств измерений
|

