| Общая информация » Каталог студенческих работ » ТЕХНИЧЕСКИЕ ДИСЦИПЛИНЫ » Начертательная геометрия и инженерная графика |
| 07.01.2026, 17:34 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
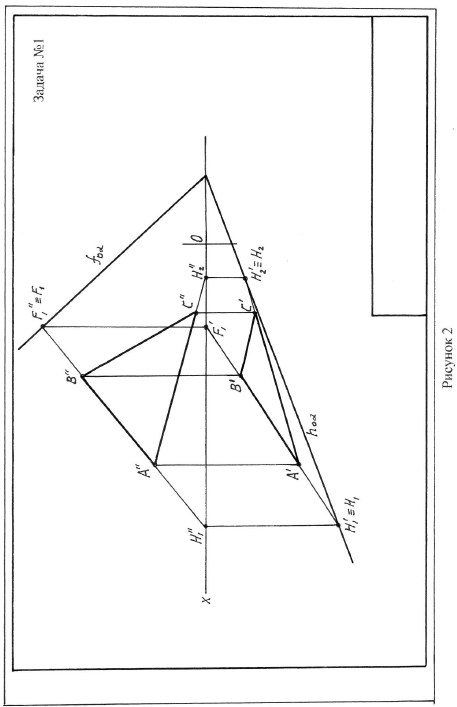
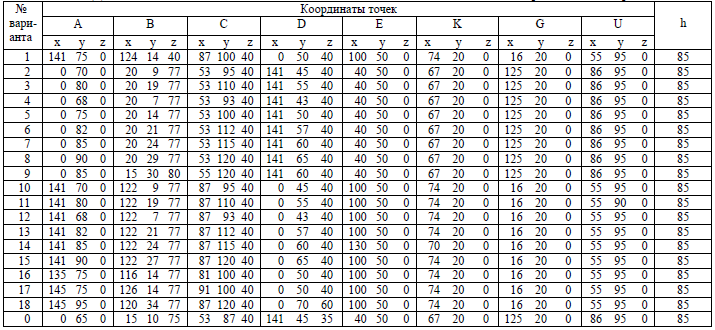
Студенты со сроком обучения 5 лет выполняют все задачи приведенные ниже, а студенты со сроком обучения 4 года не выполняют задачи №№ 5 и 8. Номер варианта соответствует сумме двух последних цифр зачетной книжки. Например, если учебный шифр студента 17-375, то по всем задачам контрольных работ он выполняет двенадцатый (7+5=12) вариант задания. Содержание контрольной работы Задача 1. Построить следы плоскости, заданной треугольником АВС. Формат А3. Задача 2. Построить линию пересечения плоскостей, заданных треугольниками АВС и DEK и показать видимость их проекций. Формат А3. Задача 3. Построить проекции пирамиды, основанием которой является треугольник АВС, а ребро SA определяет высоту h пирамиды. Формат А3 вместе с задачей 4. Задача 4. Построить линию пересечения пирамиды с прямой призмой. Задача 5. Построить линию пересечения конуса вращения плоскостью АВС. Формат А3 вместе с задачей 6. Задача 6. Построить линию пересечения конуса вращения с цилиндром вращения. Задача 7. Построить линию пересечения закрытого тора с поверхностью наклонного цилиндра вращения. Формат А4. Задача 8. Построить линию пересечения открытого тора с поверхностью конуса вращения. Формат А4. Пояснения к выполнению задач Задача 1. По координатам точек из приложения А строятся фронтальная и горизонтальная проекции треугольника АВС. Следы плоскости, заданной треугольником АВС, определяются по следам двух любых сторон треугольника. Следом прямой называется точка пересечения прямой с плоскостью проекций. Фронтальный след F прямой определяется по его горизонтальной проекции F’, которая определяется как точка пересечения горизонтальной проекции прямой с осью x. Горизонтальный след Н прямой определяется по его фронтальной проекции Н”, которая определяется как точка пересечения фронтальной проекции прямой с осью x. Каждый след плоскости строится по двум точкам. Пример выполнения задачи 1 приведен на рисунке 2.
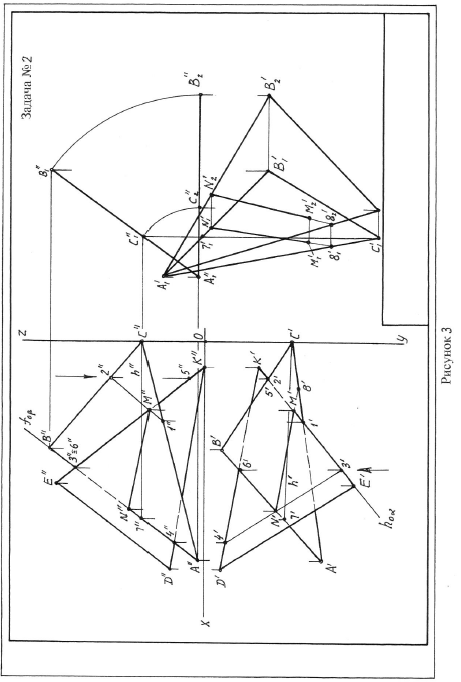
Задача 2. По координатам точек из приложения А строятся проекции треугольников АВС и DEK. Линия пересечения двух плоскостей, заданных треугольниками АВС и DEK, строится по двум точкам. Для этого определяются точки пересечения двух любых сторон одного треугольника с другим треугольником. Для определения точки пересечения прямой с плоскостью заключается эта прямая в проецирующую плоскость, строятся проекции линии пересечения проецирующей плоскости с треугольником. Точка пересечения этой линии с прямой, заключѐнной в проецирующую плоскость, и есть точка пересечения прямой с треугольником. Аналогично определяется вторая точка. Видимость сторон треугольников определяется методом конкурирующих точек. Для этого берѐтся точка скрещивания, например, фронтальных проекций двух любых сторон треугольников и по горизонтальным проекциям точек на этих прямых определяется расположение этих прямых на фронтальной плоскости проекций. Видимость сторон треугольников на горизонтальной плоскости проекций определяется по точкам скрещивания двух любых сторон треугольников на горизонтальной плоскости проекций. Натуральная величина треугольника АВС определяется двумя этапами. На первом этапе треугольник плоскопараллельным перемещением переводится во фронтально проецирующее положение, для чего строятся проекции горизонтали, принадлежащей треугольнику АВС, и горизонтальная проекция треугольника поворачивается так, чтобы горизонтальная проекции h’ стала перпендикулярной оси x. На втором этапе способом вращения треугольника вокруг перпендикуляра к плоскости проекций p 1 и есть натуральная величина треугольника АВС. Пример выполнения задачи 2 приведен на рисунке 3.
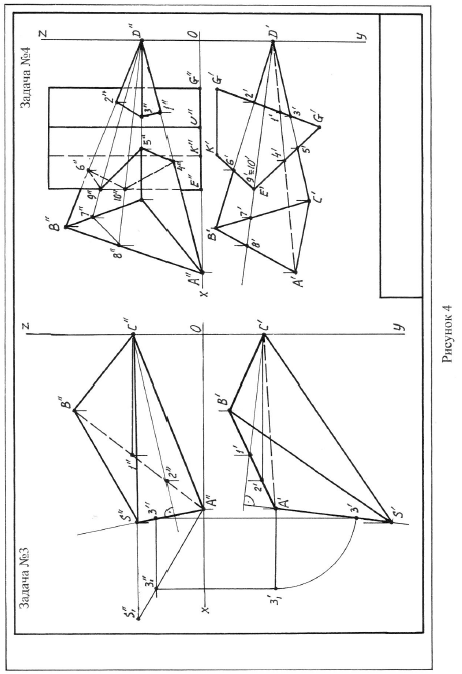
Задача 3. По координатам точек из приложения Б строятся фронтальная и горизонтальная проекции основания пирамиды АВС. Строятся проекции горизонтали и фронтали, принадлежащих треугольнику АВС. Из точки А восстанавливается перпендикуляр к плоскости. Фронтальная проекция перпендикуляра перпендикулярна фронтальной проекции f” фронтали, горизонтальная проекция перпендикуляра перпендикулярна горизонтальной проекции h’ горизонтали. На перпендикуляре откладывается произвольный отрезок и способом вращения вокруг перпендикуляра к любой плоскости проекций определяется его натуральная величина. На направлении натуральной величины отрезка откладывается высота пирамиды, а затем обратным порядком определяется положение проекций S’ и S” вершины пирамиды. Видимость рѐбер пирамиды определяется методом конкурирующих точек, как в задаче №2. Пример выполнения задачи 3 приведен на рисунке 4.
Задача 4. По координатам точек из приложения В строятся проекции призмы и пирамиды. Так как грани призмы занимают горизонтально- проецирующее положение, то горизонтальная проекция линии пересечения поверхностей совпадает с горизонтальной проекцией призмы. Поэтому отмечаем точки 1,2,3,4,5,6 на пересечении ребер пирамиды с гранями призмы. Для построения точек 9 и 10, в которых ребро призмы Е пересекает пирамиду, заключаем эти точки во вспомогательные прямые D7 и D8, строим их фронтальные проекции и на пересечении их с ребром Е находим искомые точки 9 и 10. Соединяем точки линии пересечения с учетом их видимости, учитывая видимость соответствующих граней призмы и пирамиды. Пример выполнения задачи приведен на рисунке 4.
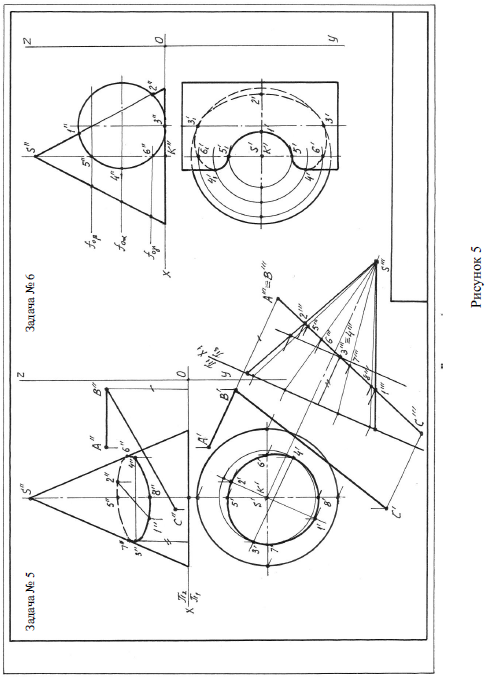
Задача 5. По координатам точек из приложения Г строятся проекции конуса (высота h и радиус R) плоскости, заданной пересекающимися прямыми.. Способом замены фронтальной плоскости проекций p 2 на p 3 переводится секущая плоскость общего положения во фронтально проецирующее. Для этого ось x1 проводится перпендикулярно проекции А’B’ прямой АВ. На плоскости проекций p 3 сечение конуса секущей плоскостью совпадает со следом этой плоскости. По точкам пересечения характерных образующих конуса секущей плоскостью на плоскости проекций p 3 определяются эти точки на образующих конуса на плоскостях проекций p 1 и p 2. Последовательным соединением точек строятся проекции линии взаимного пересечения конуса и плоскости с учѐтом видимости линий. Пример выполнения задачи приведен на рисунке 5.
Задача 6. По координатам точек из приложения Д строятся проекции конуса (высота h радиус основания R) и цилиндра (радиус R1). Определяются проекции опорных точек взаимного пересечения фигур (для примера на рисунке 6 – точки 1, 2, 3). Дополнительные точки определяются с помощью горизонтальных секущих плоскостей, которые пересекают конус по окружностям, а цилиндр – по образующим. Пересечением соответствующих окружностей и образующих на горизонтальной плоскости проекций и определяются общие точки конуса и цилиндра. Так как цилиндрическая поверхность является фронтально проецирующей, то на плоскости p 2 линия пересечения конуса с цилиндром совпадает с фронтальной проекцией цилиндра. Горизонтальная проекция линии пересечения поверхностей строится по построенным точкам. Пример выполнения задачи 6 приведен на рисунке 5.
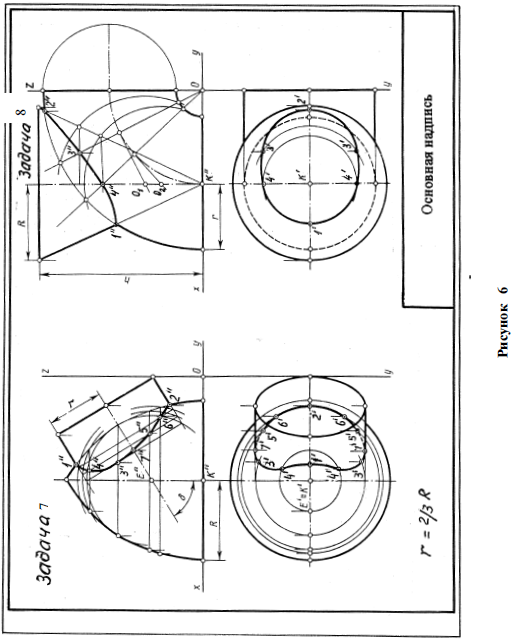
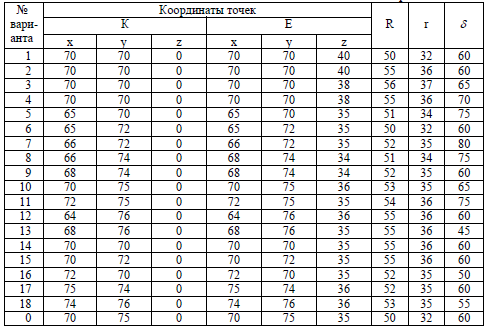
Задача 7. По координатам точек и размерам из приложения Е строятся проекции закрытого тора (радиус основания R) и цилиндра (радиус r, угол наклона оси к вертикали d ). Точки 1 и 2 являются опорными точками взаимного пересечения поверхностей, так как оси тора и цилиндра лежат в одной фронтальной плоскости и пересекаются в точке Е. Промежуточные точки взаимного пересечения фигур определяются способом вспомогательных секущих сферических поверхностей. Проекции сфер строятся на плоскости проекцийp 2. Сфера минимального радиуса должна быть такой, чтобы она коснулась очерка тора и пересекла очерк цилиндра. В этом случае сфера касается тора по горизонтальной окружности, а цилиндр пересекает по фронтально проецирующей окружности. Взаимное пересечение этих окружностей на плоскости проекций p2 даѐт точку 3”,по которой и горизонтальной проекции окружности на торе определяются проекции точек 3’ (их две). Дополнительные точки определяются построением фронтальных проекций сфер большего радиуса, но не выходящих за пределы опорных точек (1” и 2”). Пример выполнения задачи приведен на рисунке 6.
Задача 8. По координатам точек и размерам приложения Ж строятся проекции части открытого тора (радиус сечения r) и конуса (радиус R, высота h). Так как ось образующей тора и конуса лежат в одной фронтальной плоскости, то проекции линии пересечения фигур определяются способом вспомогательных секущих сферических поверхностей. Точки 1 и 2 для примера, приведенного на рисунке 7, являются опорными. На окружной оси тора берутся несколько точек (в примере на рисунке 7 взято две точки) и через них проводятся касательные к этой оси и лучи через центр тора. Пересечение касательных с осью конуса на плоскости проекций p 2 даѐт центры соответствующих сфер (точки О1 и О2). Радиус сферы определяется расстоянием от центра сферы до пересечения луча с очерком тора. Сфера пересекает конус по горизонтальной окружности, а тор – по фронтально проецирующей окружности. Взаимное пересечение этих окружностей даѐт искомые точки взаимного пересечения фигур (на примере точки 3” и 4”). Горизонтальные проекции этих точек определяются на горизонтальных проекциях окружностей сечения конуса сферами.
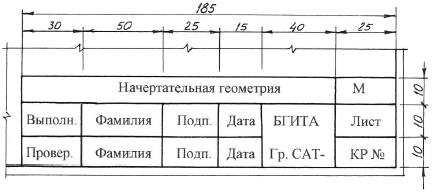
Все чертежи контрольной работы № 1 сопровождаются основной надписью по форме, приведенной на рисунке 7.
Рисунок 7
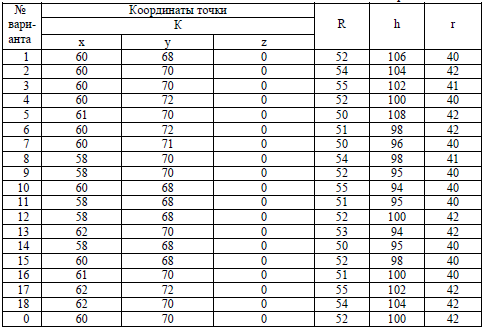
Приложение А (обязательное) Таблица А.1 – Данные для задач 1 и 2 Размеры в миллиметрах
Приложение Б (обязательное) Таблица Б.1 – Данные для задачи 3 Размеры в миллиметрах
Приложение В (обязательное) Таблица В.1 – Данные к задаче 4 Размеры в миллиметрах
Приложение Г (обязательное) Таблица Г.1 – Данные к задаче 5 Размеры в миллиметрах
Приложение Д (обязательное) Таблица Д.1 – Данные к задаче 6 Размеры в миллиметрах
Приложение Е (обязательное) Таблица Е.1 – Данные к задаче 7 Размеры в миллиметрах
Приложение Ж (обязательное) Таблица Ж.1 – Данные к задаче 8 Размеры в миллиметрах
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||