СГТУ, сопротивление материалов (расчетно-графическая работа)

Для пользования таблицей 1 (Приложение 1), надо записать номер своего студенческого билета или зачётной книжки и под ним первые шесть букв русского алфавита, например: 

Тогда  а = 1; б = 3; в = 2; г = 7; д = 10; е = 4.

Из каждого вертикального столбца таблицы 1 (Приложение 1), надо взять только одно число, стоящее в той горизонтальной строке, номер которой совпадает с номером расположенной внизу буквы. Например, вертикальные столбцы таблицы обозначены буквами: е, г, д. В этом случае, при указанном выше номере студенческого билета 1 2 3 7 0 4, студент должен взять из столбца е строку номер 4, из столбца г – строку  номер 7 и из столбца д – строку номер 10.

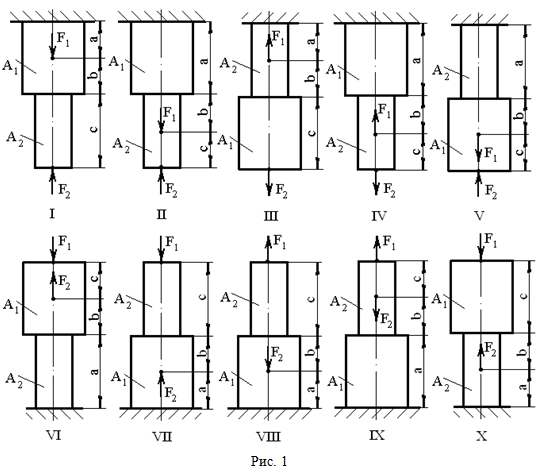
ЗАДАЧИ ДЛЯ РАСЧЕТНО-ГРАФИЧЕСКИХ И КОНТРОЛЬНЫХ РАБОТ

РАСЧЕТ СТУПЕНЧАТОГО БРУСА НА РАСТЯЖЕНИЕ–СЖАТИЕ

(Тема: «Центральное растяжение-сжатие». Раздел: «Статически определимые системы».)

Для  ступенчатого  стального  бруса  круглого  поперечного  сечения, (рис. 1), выполненного из стали марки Ст. 3, имеющей предел текучести   s_Т, модуль Юнга E, требуется:

1) построить по длине бруса эпюры продольных сил N, нормальных напряжений s и перемещений поперечных сечений d;

2) вычислить коэффициент запаса прочности бруса n.

Принять: а = 0,1ℓ₁; в = 0,1ℓ₂; с = 0,1ℓ₃. 

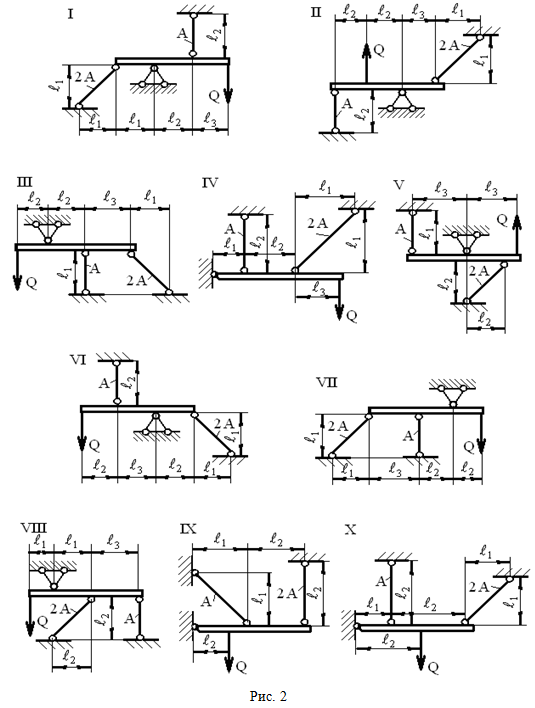
РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ  СТЕРЖНЕВОЙ СИСТЕМЫ

(Тема: «Центральное растяжение-сжатие». Раздел: «Статически неопределимые системы».)

Абсолютно жесткий брус (рис. 2) оперт на шарнирно-неподвижную опору и прикрепляется к двум стержням, при помощи шарниров. Стержни изготовлены из стали марки Ст. 3,

Требуется:

1) найти усилия и напряжения в стержнях, выразив их через силу Q;

2) из расчета по допускаемым напряжениям найти допускаемую нагрузку [Q], приравняв большее из напряжений в двух стержнях к допускаемому напряжению [σ];   

3) из расчета по допускаемым нагрузкам найти предельную грузоподъемность системы Q_T^k  и   допускаемую нагрузку Q_ДОП, если известен предел текучести  σ_Т  и коэффициент запаса прочности   n = 1,5;

4) сравнить величины [Q] и  Q_ДОП, полученные при расчете по допускаемым напряжениям  и допускаемым нагрузкам.

Принять: А = А₁.

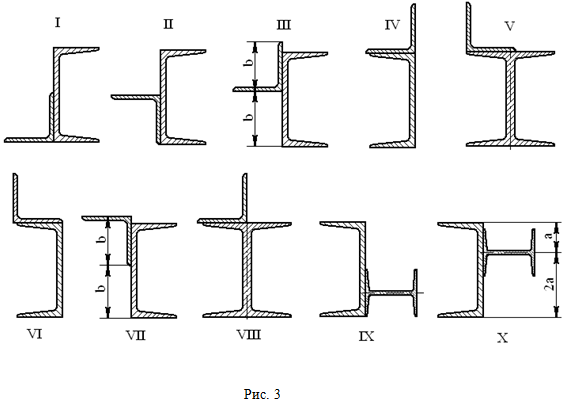
ОПРЕДЕЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК ПЛОСКИХ СЕЧЕНИЙ

(Тема: «Геометрические характеристики плоских сечений».)

Задано поперечное сечение, состоящее из двух профилей, имеющих вид швел­лера, двутавра или равнополочного уголка (рис. 3),

Требуется:

1) определить положение центра тяжести поперечного сечения;

2) найти осевые и центробежный моменты инерции относительно случайных осей (x_C и y_C), проходящих через центр тяжести;

3) определить положение главных централь­ных осей u и v;

4) найти моменты инерции относительно главных центральных осей;

5) вычертить сечение и указать на нем все размеры в числах и все оси.

При расчете все необходимые данные следует брать из таблиц сортамента.

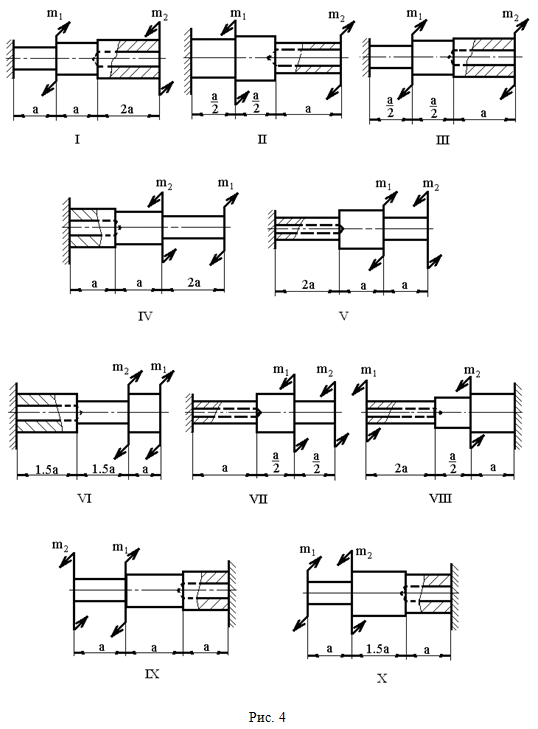
РАСЧЕТ ВАЛА НА КРУЧЕНИЕ

(Тема: «Сдвиг и кручение».)

Стальной  вал, закручивается двумя моментами m₁  и  m₂ (рис. 4). Два участка  вала имеют  форму поперечного сечения  в виде кругов диаметрами d₁ и d₂, а третий участок вала полый - имеет  форму поперечного сечения в виде кольца с заданным отношением внутреннего диаметра d к наружному D. 

Требуется:

1) построить эпюру крутя­щих моментов М_К;

2) из условия прочности по допускаемым касательным напряжениям  [τ] определить размеры поперечных сечений участков вала и округлить их до ближайшей большей  величины в мм;

3) построить эпюру углов поворота α.

Принять: а = 0,1ℓ₃.

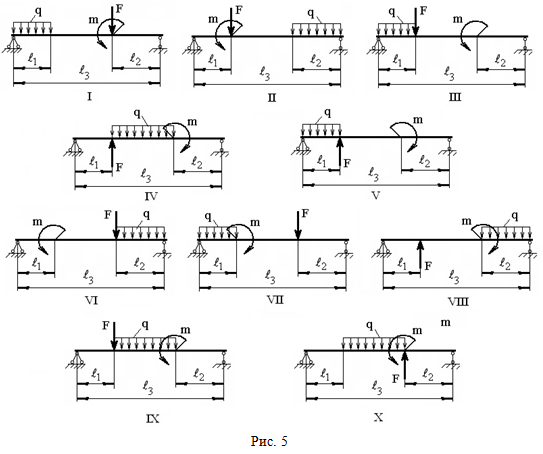
РАСЧЕТ ШАРНИРНО-ОПЕРТОЙ БАЛКИ НА ИЗГИБ

(Тема: «Изгиб».)

Стальная балка, изображена на рис. 5.

Требуется:

1) построить эпюры поперечной силы Q_У и изгибающего момента М_Х;

2) подобрать из условия прочности по допускаемым напряжениям поперечные сечения в виде круга, квадрата, двутавра и двух швеллеров;

3) сравнить принятые сечения балок по экономичности.

Стенки двутавра и двух швеллеров параллельны действующей нагрузке.

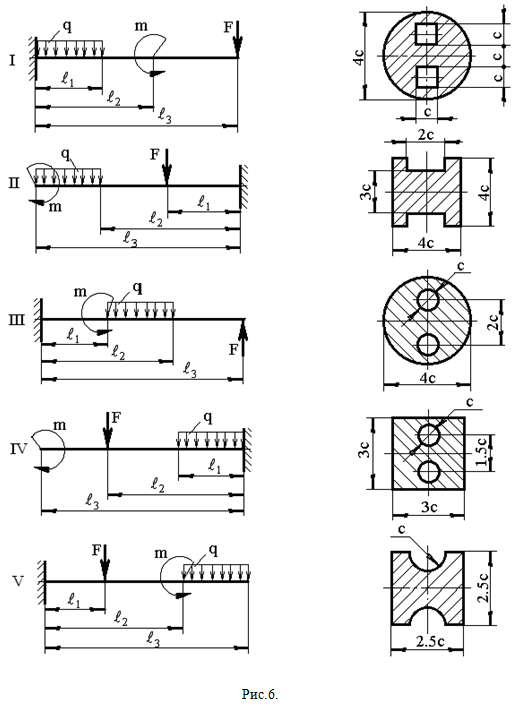
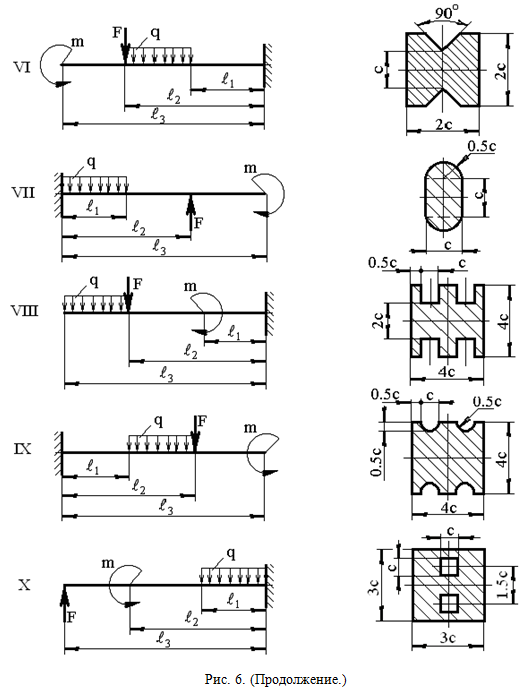
РАСЧЕТ БАЛКИ-КОНСОЛИ НА ИЗГИБ

(Тема: «Изгиб».)

Стальная балка, изображена на рис. 6.

Требуется:

1) построить эпюры поперечной силы Q_У и изгибающего момента М_Х;

2) подобрать из условия прочности по допускаемым напряжениям сложное поперечное сечение, изображенное справа от схемы балки.

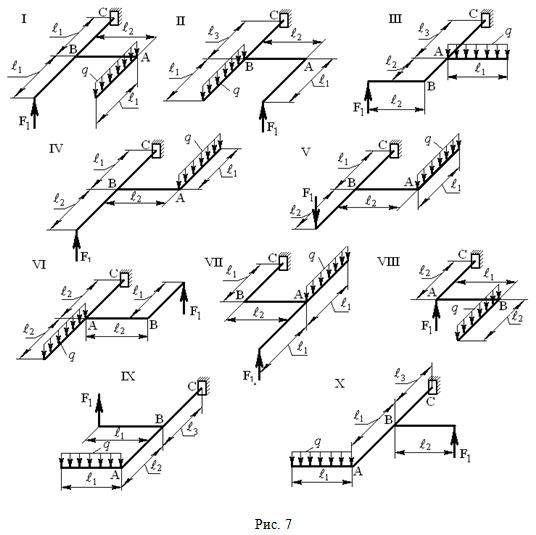
РАСЧЕТ ПРОСТРАНСТВЕННОГО ЛОМАНОГО БРУСА

 (Тема: «Изгиб». Раздел: «Изгиб с кручением».)

На рис. 7 изображена в аксонометрии ось ломаного стержня круг­лого поперечного сечения, расположенная в горизонтальной плоскости и имеющая прямые углы в точках А и В. На стержень действует вер­тикальная нагрузка F₁ и q.

Требуется:

1) построить отдельно (в аксономет­рии) эпюры изгибающих и крутящих моментов;

2) установить опасное сечение и найти для него величину расчетного момента по энергетическому критерию.

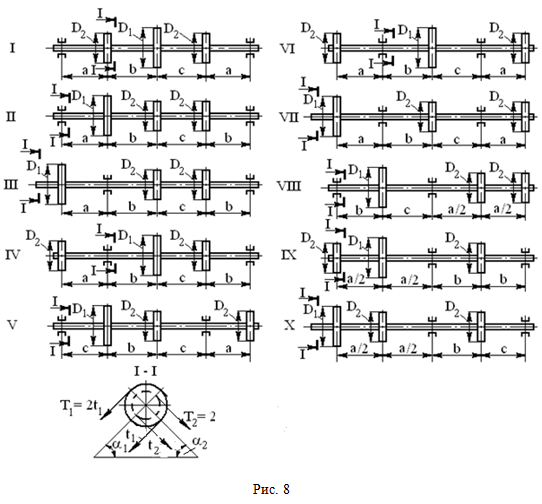
РАСЧЕТ ВАЛА НА ИЗГИБ С КРУЧЕНИЕМ

(Тема: «Изгиб». Раздел: «Изгиб с кручением».)

Шкив диаметром D₁ и углом наклона ветвей ремня к  горизонту α₁ делает n оборотов в минуту и передает мощность N кВт. Два других шкива имеют одинаковый диаметр D₂ и одинаковые  углы наклона ветвей ремня к горизонту α₂ и каждый из них передает мощность N/2 кВт (рис. 8).

Требуется:

1) определить моменты, приложенные к шкивам, по заданным N и n;

2) построить эпюру крутящих мо­ментов М_К;

3) определить окружные усилия t₁ и t₂, действующие на шкивы, по найденным моментам и заданным диаметрам шкивов   D₁  и   D₂;    

4) определить давления на вал, принимая их равными трем окружным усилиям;

5) определить силы изгибающие вал в горизонтальной и вертикальной плоскостях (вес шкивов и вала не учитывать);

6) построить эпюры изгибающих моментов от горизонтальных сил М_ГОР и от вер­тикальных сил М_ВЕРТ;

7) построить эпюру суммарных изгибающих момен­тов, пользуясь формулой (для каждого попереч­ного сечения вала имеется своя плоскость действия суммарного изги­бающего момента, но для круглого сечения можно совместить плоско­сти М_ИЗГ для всех поперечных сечений и построить суммарную эпюру в плоскости чертежа; при построении эпюры надо учесть, что для не­которых участков вала она не будет прямолинейной);

8) при помощи эпюр М_К и М_ИЗГ найти опасное сечение и опре­делить величину максимального расчетного момента по критерию наибольших касательных напряжений;

9) подобрать из условия прочности по допускаемым напряжениям диаметр вала и округлить до ближайшей большей величины кратной 10 мм.

Принять: а = 0,2ℓ₁; в = 0,2ℓ₂; с = 0,2ℓ₃; D₁ = 0,5ℓ₁; D₂ = 0,5ℓ₂. 

РАСЧЕТ СТЕРЖНЯ НА УСТОЙЧИВОСТЬ

 (Тема: «Устойчивость сжатых стержней».)

Стальной стержень (рис. 9) длиной ℓ сжимается силой F и имеет сложное поперечное сечение, изображенное справа на рис. 6.  

Требуется:

1) найти размеры поперечного сечения при допускаемом напряжении [σ]. Расчет производить методом последовательных приближений, предварительно задавшись коэффициентом уменьшения допускаемых напряжений    φ = 0,5;

2) найти критическую силу F_K и коэффициент запаса устойчивости n_У.

Принять: ℓ = 0,7ℓ₁; F = F₂. 

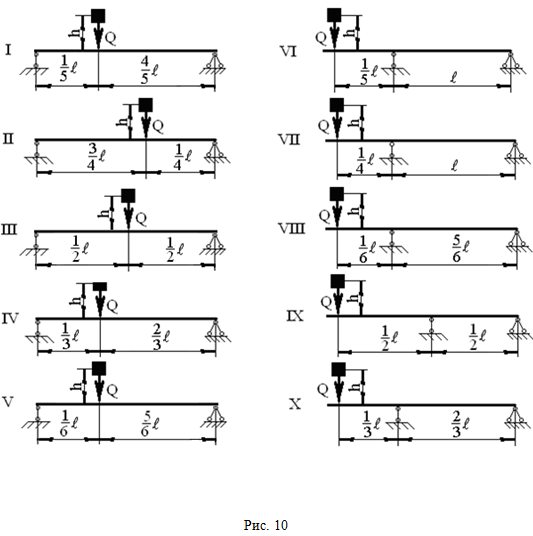
РАСЧЕТ НА УДАР

 (Тема: «Динамическое действие нагрузок». Раздел: «Удар».)

На двутавровую балку, свободно лежащую на двух жестких опорах (рис. 10), с высоты h падает груз весом Q.

Требуется:

1) найти наибольшее нормальное напряжение в балке;

2) решить аналогичную задачу при условии, что левая опора заменена пружиной, податливость которой (т. е. осадка от груза весом 1 кН) равна α =0,02 м/кН;

3) сравнить полученные результаты.

Принять: Q = 0,01F₂; h = 0,1ℓ₁; ℓ = ℓ₁.

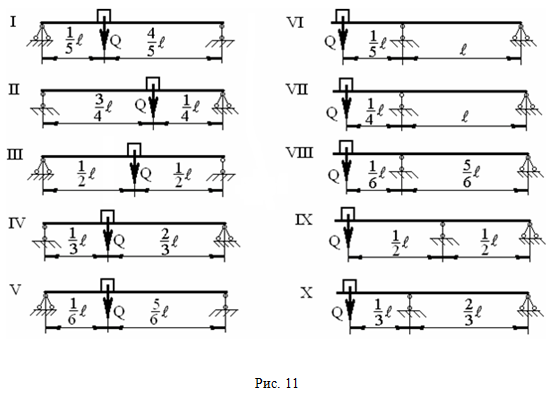
РАСЧЕТ НА КОЛЕБАНИЯ

(Тема: «Динамическое действие нагрузок». Раздел: «Колебания».)

На двух балках двутаврового сечения установлен двигатель ве­сом Q (рис. 11), делающий n оборотов в минуту. Центробежная сила инерции, возникающая вследствие неуравновешенности вращающихся частей двигателя, равна Н. Собственный вес балок и силы сопротивления можно не учитывать.

Требуется найти:

1) частоту собственных колебаний ω₀;

2) частоту изменения возмущающей силы ω;

3) коэффициент нарастания колебаний (если коэффициент β, определяемый по этой формуле, окажется отрицательным, то в даль­нейшем расчете следует учитывать его абсолютную величину);

4) дина­мический коэффициент;

5) наибольшее нормальное напряжение в балках σ_Д = К_Д · σ_СТ .

Принять:   Q = 0,1F₂; H = 0,1F₁; ℓ = ℓ₁.

Приложение 1

Таблица 1

Таблица 1 (Продолжение)

Значения некоторых величин, используемых при решении задач.

Модуль Юнга стали  E = 2×10⁵ MПа. 

Модуль сдвига стали   G = 0,8·10⁵ МПа.

Предел текучести стали марки Ст. 3  σ_Т = 240 МПа.

Допускаемое нормальное напряжение   [σ] = 160 МПа.

Допускаемое касательное напряжение   [τ] = 80 МПа.