Исходные данные для решения задач выбираются из таблиц, приведенных в разделе № 3 учебного пособия, в соответствии с личным шифром студента и первыми шестью буквами русского алфавита, которые следует расположить под шифром. Личный шифр студента соответствует номеру, указанному в зачетной книжке, например:

Из каждого вертикального столбца таблицы данных, обозначенного внизу определенной буквой, следует взять число в той горизонтальной строке, номер которой совпадает с номером буквы в личном шифре студента.

Предлагаемые для решения задачи объединены в четыре контрольные работы.

Количество контрольных работ, выполняемых в семестре, определяется согласно графику учебного процесса.

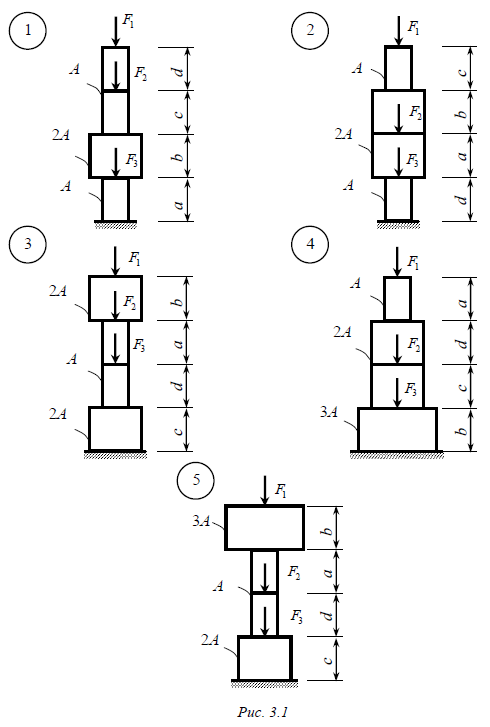
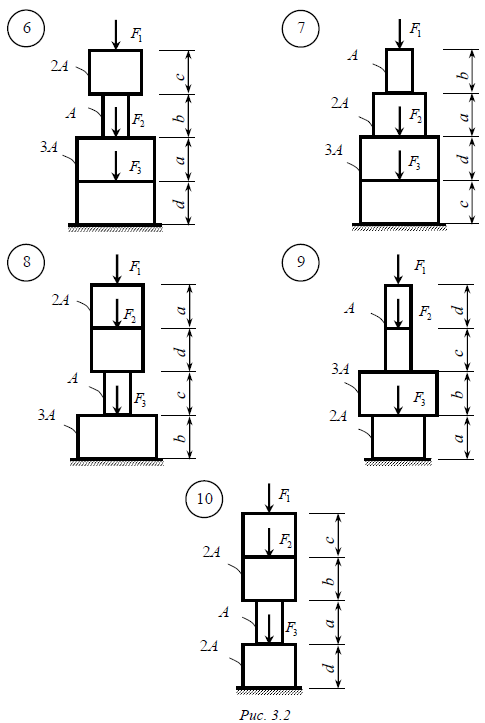
ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ РАБОТ

Задача № 1

Ступенчатая колонна квадратного поперечного сечения (рис.  3.1,  3.2)  выполнена из  бетона с модулем  упругости E = 2,0 ×10⁴ МПа и загружена сосредоточенными силами F₁, F₂ , F₃. Требуется:

1. Построить эпюру продольных сил.

2. Определить площади поперечных сечений колонны, учитывая, что материал, из которого она изготовлена, неодинаково работает на растяжение и сжатие (расчетное сопротивление материала сжатию Rсж = 10 МПа; растяжению Rр = 1,2 МПа ).

3. Построить эпюру нормальных напряжений.

4. Построить эпюру вертикальных перемещений сечений колонны.

Исходные данные для решения задачи определить согласно шифру по табл. 3.1.

Таблица 3.1

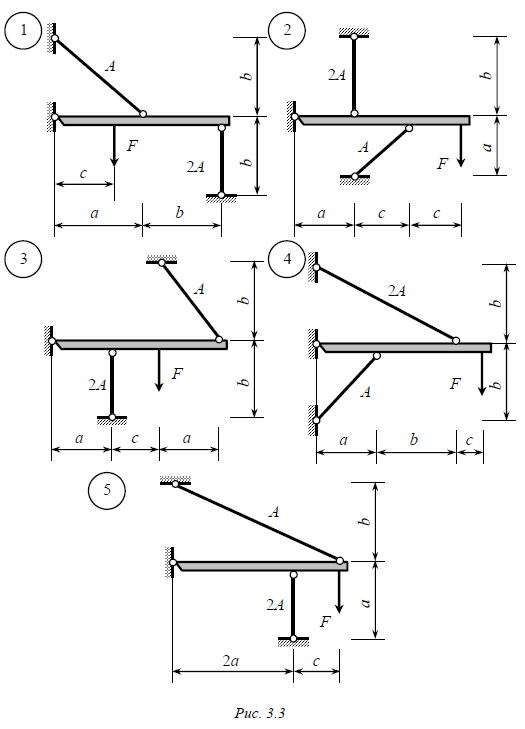
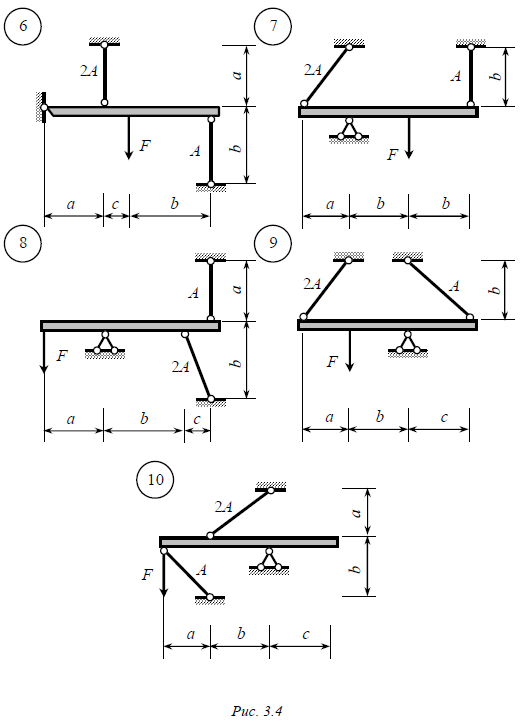
Задача № 2

Абсолютно жесткий брус опирается на шарнирно-неподвижную опору и прикреплен к двум стальным стержням (рис. 3.3, 3.4).

Требуется:

1. Найти усилия и напряжения в стержнях, выразив их через силу F.

2. Определить  допускаемую  нагрузку  Fдоп , приравняв наибольшее из напряжений, возникающих в стержнях, расчетному сопротивлению R = 210 МПа .

3. Определить предельную нагрузку Fпред , если предел текучести материала стержней sТ = 240 МПа .

Данные взять из табл. 3.2.

Таблица 3.2

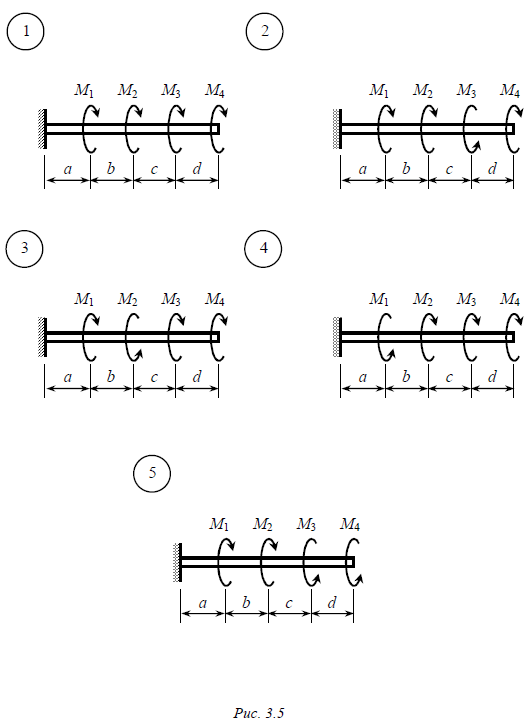
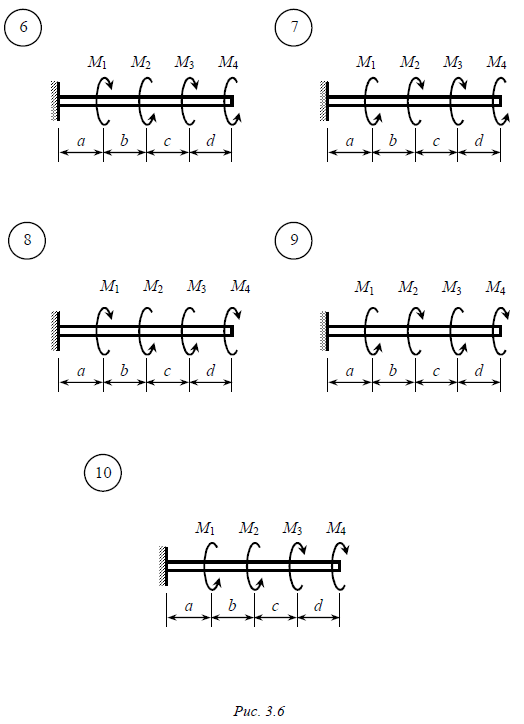
Задача № 3

К стальному валу круглого поперечного сечения приложены внешние скручивающие моменты М₁, М₂, М₃, М₄ (рис. 3.5, 3.6).

Требуется:

1. Построить эпюру крутящих моментов.

2. Определить из условия прочности диаметр вала (расчетное сопротивление материала на срез Rср ).

3. Построить эпюру углов закручивания поперечных сечений вала.

4. Найти наибольший относительный угол закручивания и проверить жесткость вала, если задано допускаемое значение относительного угла закручивания [q] .

Модуль сдвига принять G = 0,8×10⁵ МПа . Данные взять из табл. 3.3.

Таблица 3.3

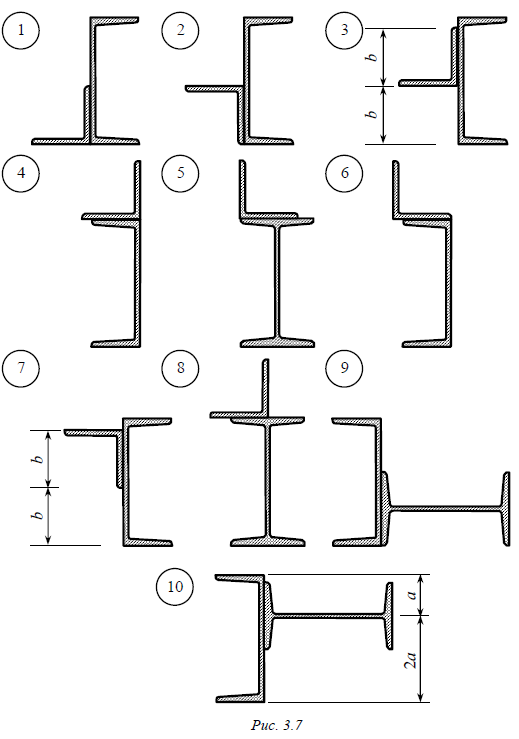
Задача № 4

Поперечное сечение элемента строительной конструкции состоит из двух прокатных профилей (рис. 3.7).

Требуется:

1. Определить положение центра тяжести сечения.

2. Вычислить осевые и центробежный моменты инерции относительно осей zC сечения. и yC , проходящих через центр тяжести

3. Определить положение главных центральных осей инерции u и v .

4. Найти значения главных центральных моментов инерции сечения.

5. Вычертить поперечное сечение в масштабе и указать все размеры и все оси координат, в том числе и главные центральные оси.

Данные взять из табл. 3.4.

Таблица 3.4

Примечание. Размеры равнополочного уголка приведены в мм.

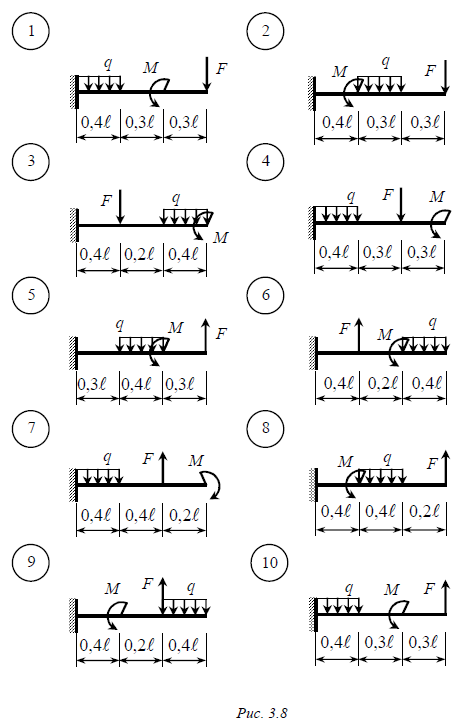
Задача № 5

Для балки-консоли (рис. 3.8) требуется:

1. Определить опорные реакции.

2. Записать в аналитическом виде выражения для внутренних усилий Qy и M z на каждом участке балки.

3. Построить эпюры внутренних усилий Qy и M z .

4. Определить размеры поперечного сечения при условии, что балка выполнена из дерева ( R = 8 МПа ) и имеет круглое поперечное сечение.

Данные взять из табл. 3.5.

Таблица 3.5

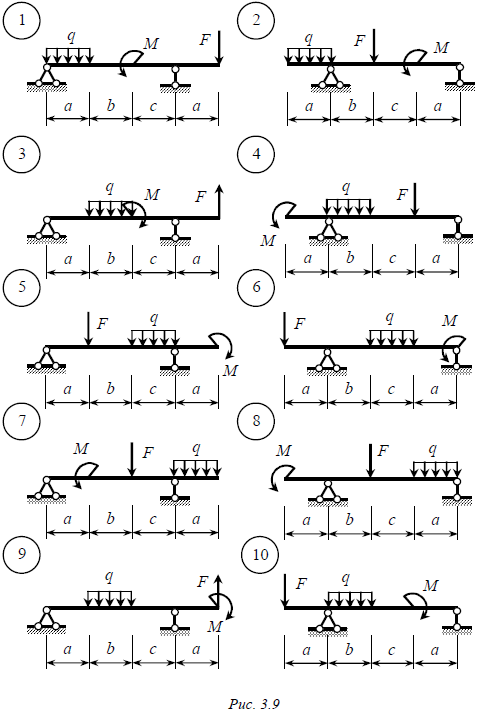
Задача № 6

Для шарнирно-опертой балки с консолью (рис. 3.9) требуется:

1. Определить опорные реакции.

2. Записать в аналитическом виде выражения для внутренних усилий Qy и M z на каждом участке балки.

3. Построить эпюры внутренних усилий Qy и M z .

4. Подобрать номер прокатного профиля двутавра из условия прочности при расчетном сопротивлении R = 210 МПа.

Данные взять из табл. 3.6.

Таблица 3.6

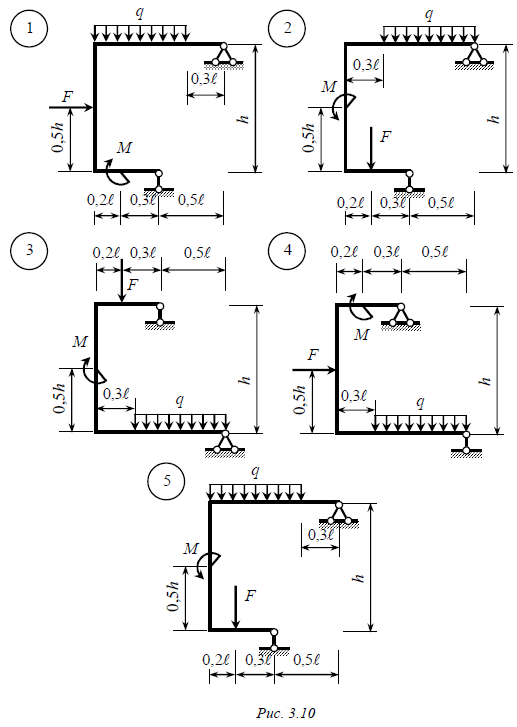
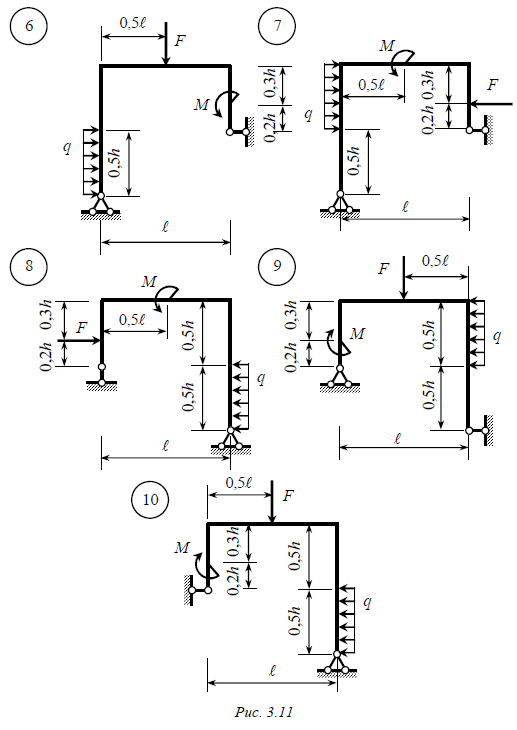
Задача № 7

Статически определимая рама, расчетная схема которой показана на рис. 3.10, 3.11, загружена внешней нагрузкой.

Требуется:

1. Определить опорные реакции.

2. Записать выражения для внутренних усилий M z , Qy и N на каждом из участков рамы.

3. Построить эпюры внутренних усилий M z , Q_y и N.

4. Выполнить проверку равновесия узлов рамы. Данные взять из табл. 3.7.

Таблица 3.7

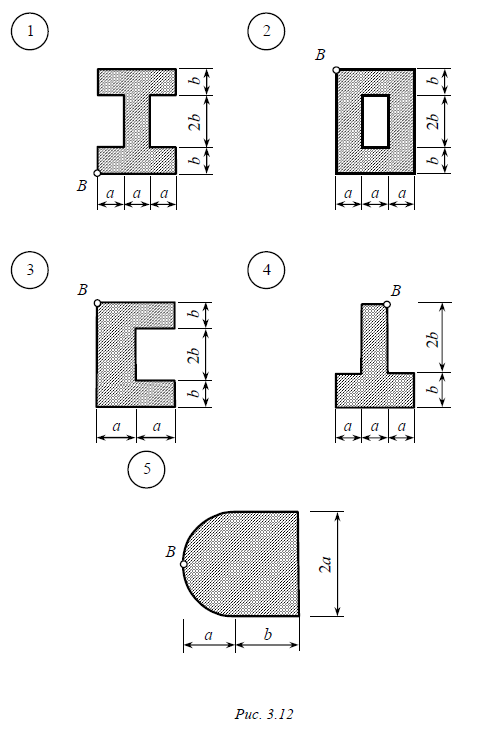
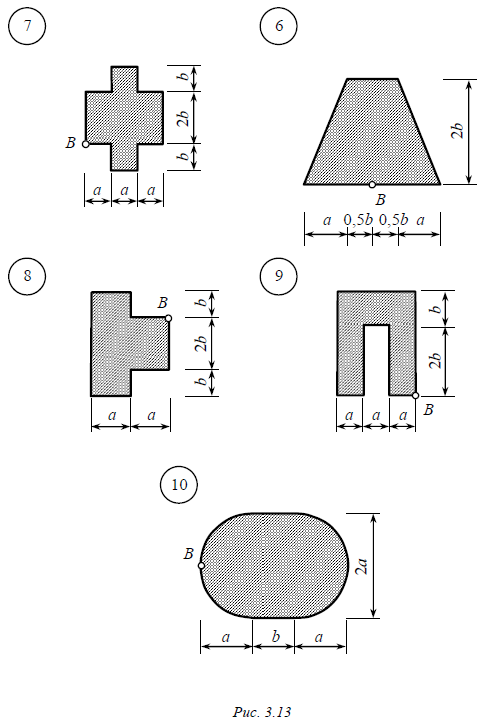
Задача № 8

Короткий стержень, поперечное сечение которого показано на рис. 3.12, 3.13, сжат продольной силой F , приложенной в точке B.

Требуется:

1. Определить положение нейтральной линии.

2. Определить в общем виде наибольшее растягивающее и наибольшее сжимающее напряжения, возникающие в поперечном сечении, выразив их через силу F.

3. Найти величину допускаемой нагрузки Fдоп при заданных размерах поперечного сечения и расчетных сопротивлений материала на сжатие Rсж и растяжение Rр.

Данные взять из табл. 3.8.

Таблица 3.8

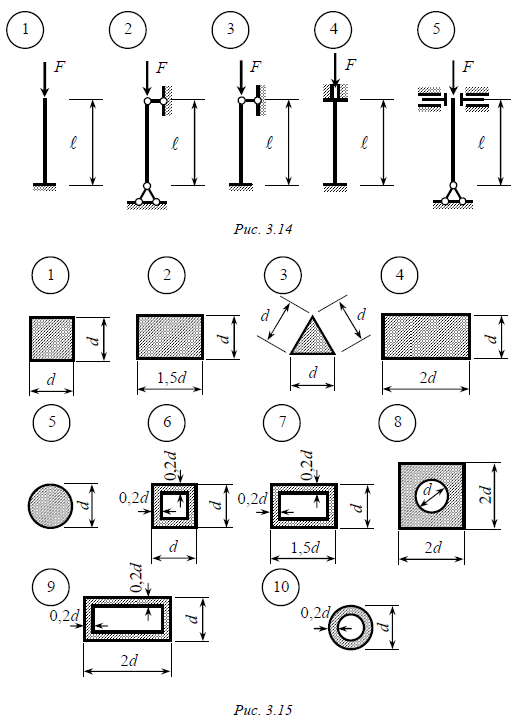
Задача № 9

Стальной стержень длиной ℓ загружен продольной силой F (рис. 3.14). Форма поперечного сечения стержня показана на рис. 3.15. При выполнении расчетов принять R = 210 МПа, E = 2 ×10⁵ МПа.

Требуется:

1. Методом последовательных приближений определить размеры поперечного сечения стержня.

2. Определить величину критической силы и коэффициент запаса по устойчивости.

Данные взять из табл. 3.9.

Таблица 3.9

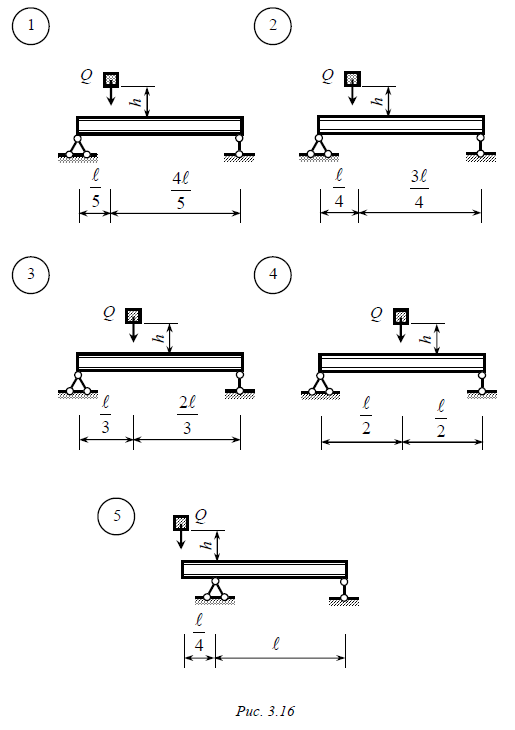
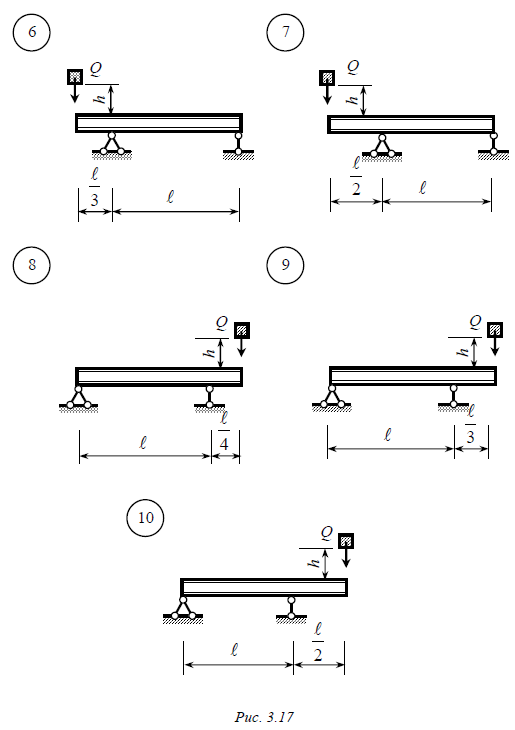
Задача № 10

На стальную двутавровую балку (рис. 3.16, 3.17) с высоты

h падает груз весом Q.

Требуется:

1. Найти наибольшие нормальные напряжения, возникающие в балке в момент удара.

2. Решить аналогичную задачу при условии, что правая опора заменена упругой с коэффициентом податливости a.

3. Сравнить полученные результаты.

Модуль упругости Е = 2 ×10⁵ МПа.

Данные взять из табл. 3.10.

Таблица 3.10