| Общая информация » Каталог студенческих работ » ТЕХНИЧЕСКИЕ ДИСЦИПЛИНЫ » Сопротивление материалов |
| 10.11.2025, 12:13 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
СОДЕРЖАНИЕ КОНТРОЛЬНЫХ ЗАДАНИЙ Расчетно-графические, контрольные и домашние работы состоят из решения практических задач по всем разделам дисциплины «Сопротивление материалов». Номера задач, которые необходимо решить студентам различных институтов, приведены в таблице 1. Таблица 1
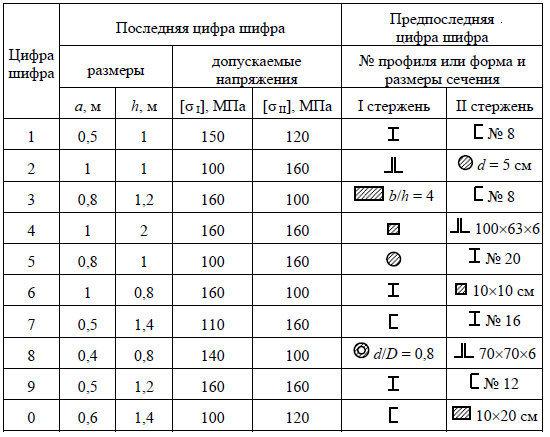
ПОРЯДОК ВЫБОРА ИСХОДНЫХ ДАННЫХ ДЛЯ ЗАДАЧ 1. Выписывается личный шифр студента (номер студенческого билета) и из всего номера берутся только 2 цифры (предпоследняя и последняя); 2. По этим цифрам шифра из таблиц выбираются числовые величины исходных данных задачи. 3. Для определения номера схемы задачи последняя и предпоследняя цифры складываются. Если сумма цифр равна 10 или более, то берется только последняя цифра суммы и по ней определяется номер схемы по таблице 2. 4. В случае, когда на схеме отсутствует какой-либо фактор (сила, момент, размер и пр.), численное значение которого имеется в таблице, то это табличное значение не принимается во внимание. Таблица 2
ЗАДАЧА № 1 Растяжение – сжатие. Расчет ступенчатого стержня Для данного стержня требуется: 1. построить эпюру продольных сил – N; 2. построить эпюру нормальных напряжений – σ; 3. построить эпюру перемещений точек, лежащих на оси стержня – Δ. Таблица к задаче № 1
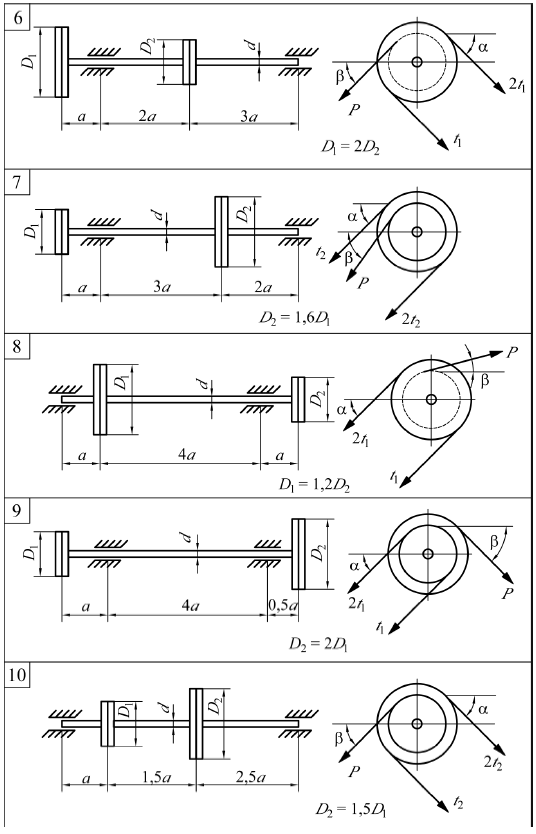
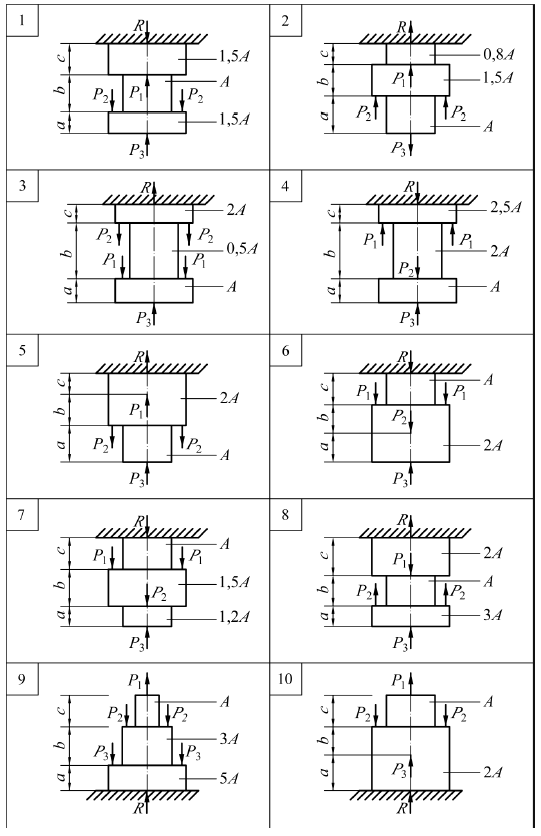
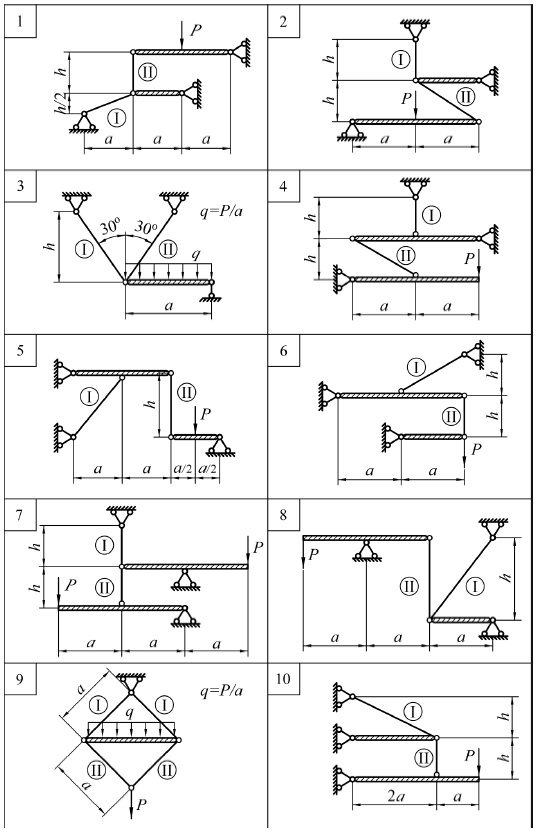
ЗАДАЧА № 2 Растяжение – сжатие. Расчет шарнирно-стержневой системы Для заданной шарнирно-стержневой системы требуется: 1. определить допускаемую нагрузку Р, исходя из прочности стержня II; 2. определить продольную силу в упругом стержне I; 3. подобрать поперечное сечение стержня I из условия прочности в форме, указанной в таблице. Примечание. Материал упругих стержней – сталь. Стержни показанные двойной линией и заштрихованные, считать абсолютно жесткими, т.е. недеформируемыми. Таблица к задаче № 2
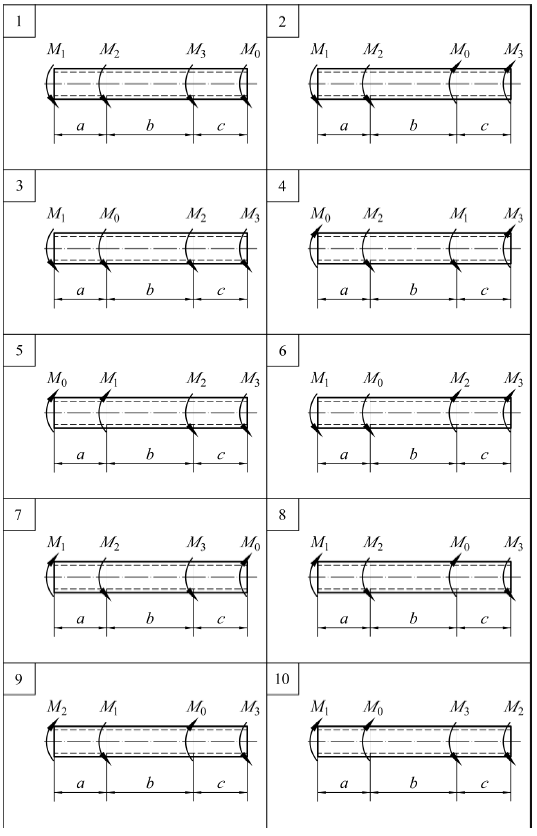
ЗАДАЧА № 3 Кручение. Расчет вала круглого поперечного сечения Стальной вал трубчатого сечения равномерно вращается со скоростью n об/мин и находится под действием четырех скручивающих внешних моментов, соответствующих передаваемым мощностям N0, N1, N2, N3. Требуется: 1. определить скручивающие моменты M0, M1, M2, M3; 2. построить эпюру крутящих моментов MK; 3. определить наружный D и внутренний d диаметры полого вала ( a = d/D ) из условия прочности по заданному допускаемому напряжению [τ] и из условия жесткости, если допускаемый относительный уровень закручивания 4. построить эпюру углов закручивания, приняв левый торец вала за неподвижный; 5. исследовать напряженное состояние элемента, расположенного на поверхности вала в окрестности точек первого участка. Таблица к задаче № 3
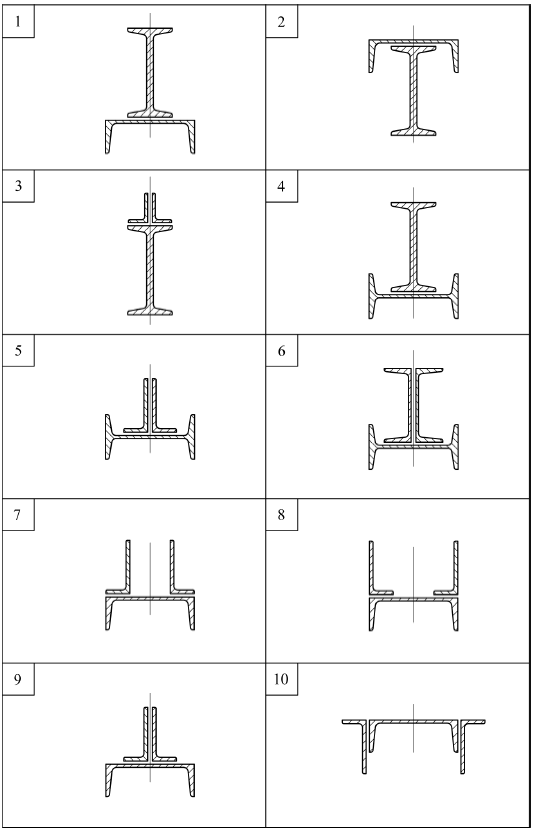
ЗАДАЧА № 4 Геометрические характеристики поперечных сечений стержней Для заданного поперечного сечения стержня, составленного из прокатных профилей, определить величины главных центральных моментов инерции. При решении использовать таблицы сортамента проката. Методические указания к решению задачи № 4 1. Вычертить сечение в масштабе 1:2 с указанием на чертеже всех заданных и необходимых для расчета размеров в числах. 2. Определить положение центра тяжести сечения, его координаты показать на чертеже. 3. Провести центральные оси, параллельные сторонам элементов прокатных профилей. 4. Пояснить, почему эти оси являются не просто центральными, а главными центральными осями. 5. Вычислить моменты инерции относительно главных центральных осей. Таблица к задаче № 4
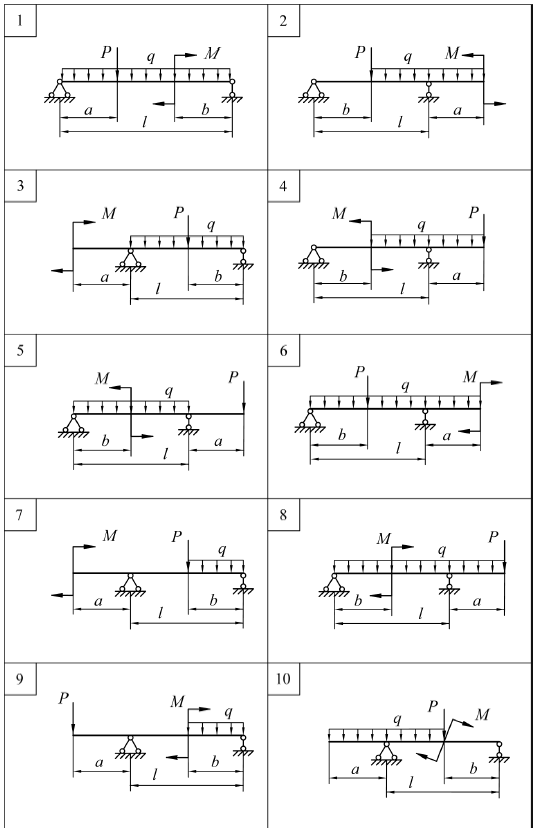
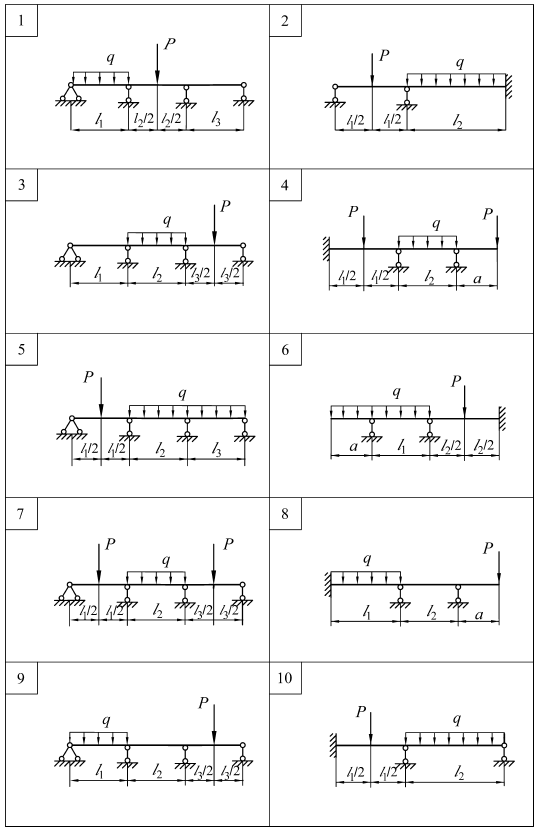
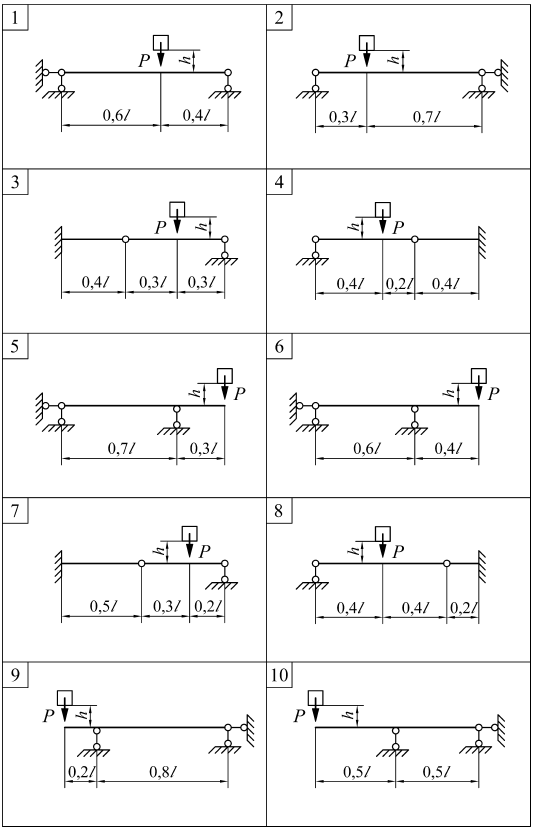
ЗАДАЧА № 5 Прямой изгиб. Построение эпюр М и Q для балки Для заданной балки требуется: 1. вычертить расчетную схему балки с соблюдением масштаба по ее длине, указать все нагрузки и размеры в цифрах; 2. определить опорные реакции; 3. отметить на схеме участки балки; 4. записать уравнения для поперечной силы Q(x) и изгибающего момента М(x) для произвольного сечения на каждом участке; 5. вычислить значения Q и М в характерных сечениях балки и построить эпюры Q и М. Таблица к задаче № 5
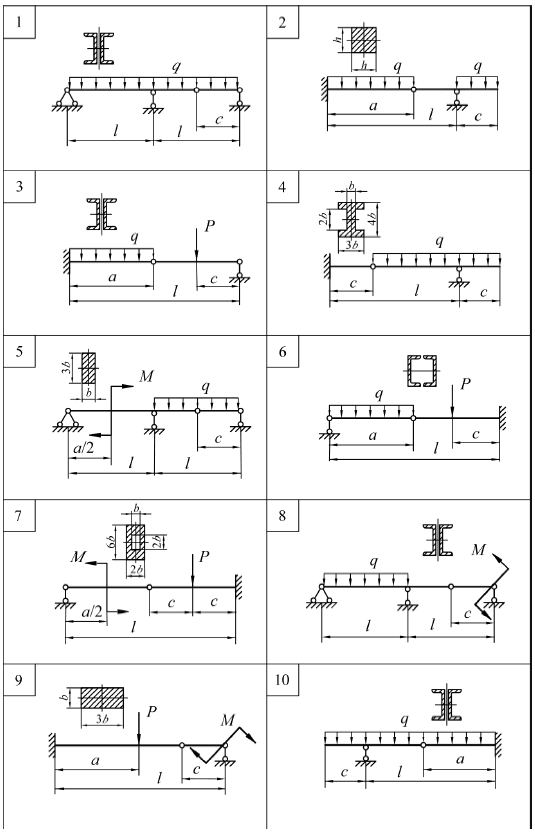
ЗАДАЧА № 6 Прямой изгиб. Расчет балки на прочность Для заданной балки требуется: 1. построить эпюры поперечных сил и изгибающих моментов; 2. подобрать из расчета на прочность по нормальным напряжениям поперечное сечение заданного прокатного или геометрического профиля, если [σ] = 160 МПа; 3. определить максимальные касательные напряжения, возникающие в балке; 4. для сечения балки, в котором поперечная сила и изгибающий момент одновременно достигают максимальных или близких к ним значений, в точке на расстоянии ¼ высоты сечения от верхнего края определить главные напряжения. Таблица к задаче № 6
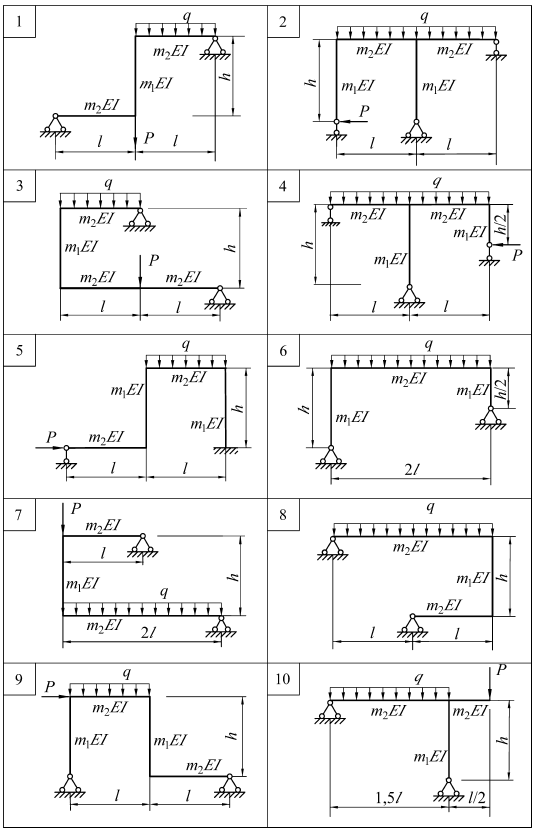
ЗАДАЧА № 7 Расчет статически неопределимой балки методом сил Для заданной балки требуется: 1. изобразить расчетную схему в масштабе, с указанием всех размеров и нагрузок в числах; 2. определить степень статической неопределимости; 3. выбрать основную и эквивалентную системы метода сил; 4. записать систему канонических уравнений метода сил; 5. построить единичные и грузовую эпюры изгибающих моментов; 6. вычислить коэффициенты при неизвестных δij и свободные члены Δip канонических уравнений; 7. решить систему канонических уравнений; 8. построить окончательную эпюру изгибающих моментов М; 9. выполнить деформационную проверку расчета; 10. построить эпюру поперечных сил Q; 11. выполнить статическую проверку расчета; 12. подобрать поперечное сечение балки из условия прочности по нормальным напряжениям в виде прокатного двутавра; 13. определить прогиб в середине первого пролета и проверить жесткость балки (для строителей); 14. определить угол поворота опорного сечения на крайней шарнирной опоре (для механиков). Таблица к задаче № 7
ЗАДАЧА № 8 Расчет статически неопределимой рамы методом сил Для заданной рамы требуется: 1. изобразить расчетную схему в масштабе и с указанием всех размеров и нагрузок в числах; 2. определить степень статической неопределимости; 3. выбрать основную и эквивалентную системы метода сил; 4. записать каноническое уравнение метода сил; 5. построить единичную и грузовую эпюры изгибающих моментов; 6. вычислить коэффициент при неизвестном δ11 и свободный член Δ1p канонического уравнения; 7. решить каноническое уравнение; 8. определить значения изгибающих моментов в характерных сечениях рамы и построить результирующую эпюру М; 9. выполнить деформационную проверку расчета; 10. построить эпюры поперечных Q и продольных N сил; 11. выполнить статическую проверку расчета. Таблица к задаче № 8
ЗАДАЧА № 9 Расчет балки на косой изгиб Для балки, работающей в условиях косого изгиба, необходимо вычислить наибольшие нормальные напряжения в опасном сечении. Примечание. Опасное сечение по длине балки может быть выражено неявно. В этом случае опасное сечение определится в результате численного исследования нормальных напряжений в предполагаемых опасных сечениях. Таблица к задаче № 9
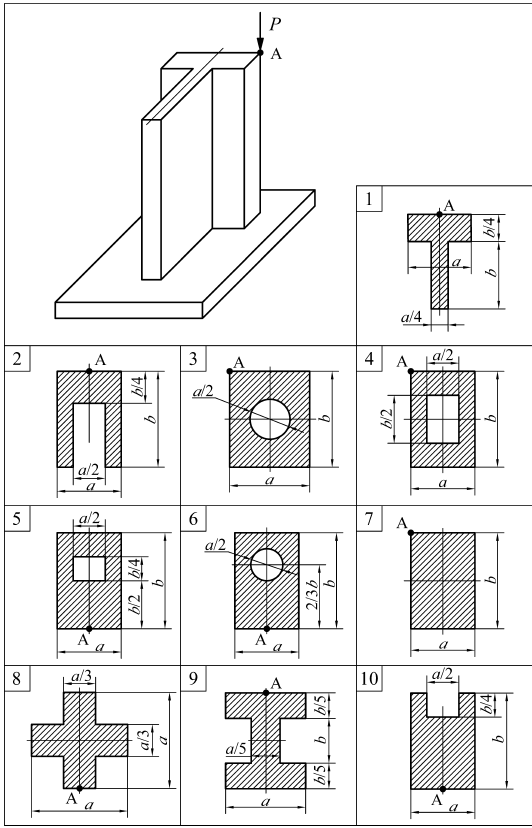
ЗАДАЧА № 10 Расчет колонны на внецентренное сжатие Колонна, поперечное сечение которой задано, нагружена сжимающей силой Р, приложенной в точке А. Требуется: 1. определить положение нейтральной линии; 2. определить наибольшие сжимающие и растягивающие напряжения; 3. построить плоскую эпюру напряжений. Таблица к задаче № 10
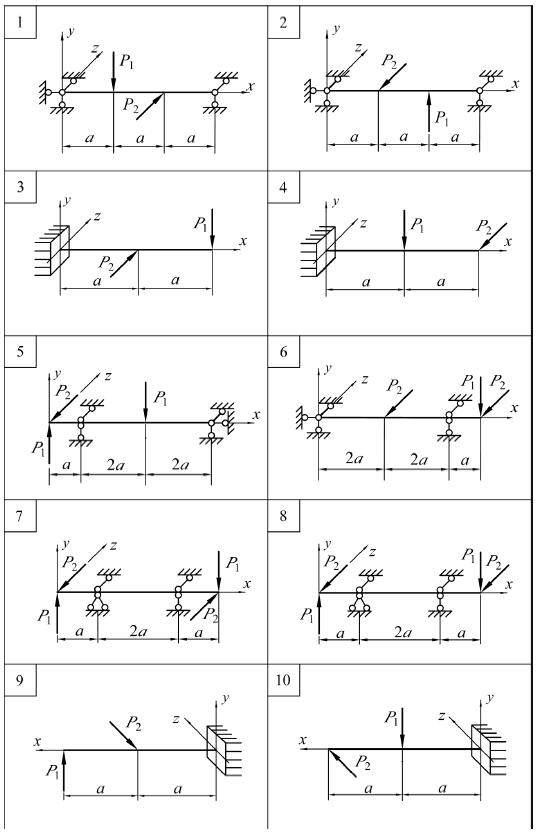
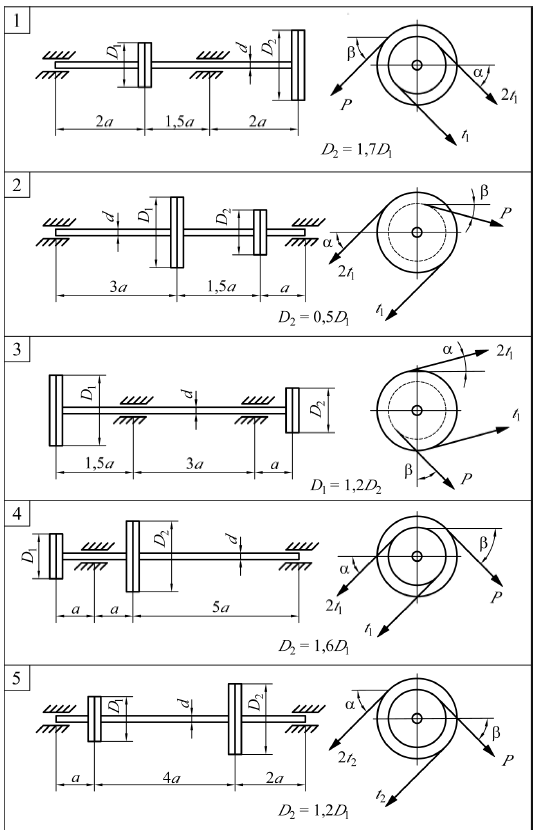
ЗАДАЧА № 11 Расчет вала на изгиб с кручением Стальной вал круглого поперечного сечения вращается со скоростью n об/мин и передает мощность N посредством зубчатого колеса с окружным усилием P и шкива, усилия в ведущей и ведомой ветвях которого соответственно равны 2t и t. Ветви ремня параллельны друг другу и наклонены к горизонту под углом α, а окружное усилие действует под углом β. Требуется: 1. изобразить расчетную схему вала и перенести на нее все внешние силы и моменты (включая реакции опор); 2. разложить окружное усилие и усилия в ветвях ремня на составляющие в вертикальной и горизонтальной плоскостях; 3. построить эпюры изгибающих и крутящих моментов; 4. установить опасное сечение вала и определить его диаметр d, используя четвертую теорию прочности. Таблица к задаче № 11
ЗАДАЧА № 12 Расчет прямолинейного сжатого стержня на устойчивость Для стойки заданного сечения, нагруженной продольной силой Р требуется определить: 1. критическую силу Ркр по формуле Эйлера или формуле Ясинского; 2. допускаемую нагрузку Рдоп, используя метод расчета с коэффициентом продольного изгиба φ. 3. коэффициент запаса устойчивости. Таблица к задаче № 12
ЗАДАЧА № 13 Расчет балки на удар На двутавровую балку падает груз весом P с высоты h. Определить наибольшее нормальное напряжение, возникающее в балке. Таблица к задаче № 13
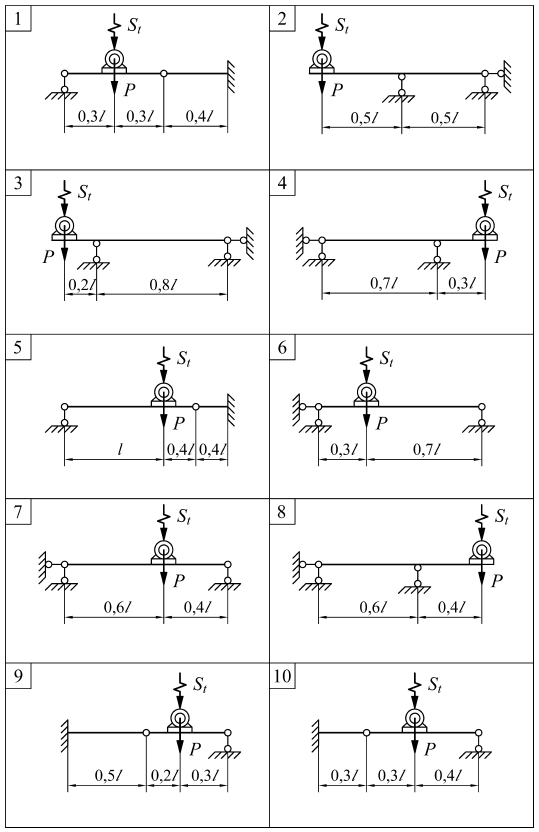
ЗАДАЧА № 14 Расчет балки на свободные и вынужденные колебания На балке, состоящей из двух двутавров, установлен двигатель весом P, делающий n оборотов в минуту. При работе двигателя возникает возмущающая периодическая сила St = S sin qt . Собственный вес балки и силы сопротивления среды не учитываются. Требуется определить: 1. частоты собственных и вынужденных колебаний ω и θ; 2. коэффициент нарастания колебаний β; 3. наибольшее полное нормальное напряжение в балке sполн. = sст.( P) + b×sст.(S ) . Примечание. Если наибольшее полное напряжение получится больше допускаемого [σ] = 160 МПа, то необходимо подобрать другой номер двутавра. Таблица к задаче № 14
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

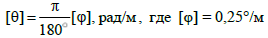 (из двух полученных значений принять наибольший диаметр);
(из двух полученных значений принять наибольший диаметр);