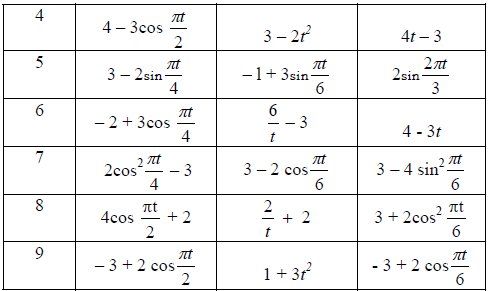Каждый вариант курсовой работы охватывает учебный материал разделов «Статика», «Кинематика» и «Динамика».

Номера условий представлены в таблицах. Студент во всех заданиях выбирает номер рисунка по предпоследней цифре своего варианта (номер варианта – две последние цифры номера зачетной книжки), а номер условия в таблице – по последней. Например, если номер зачетной книжки заканчивается цифрами 38, то во всех заданиях берутся рисунки 3 и условия 8 из таблиц.

Структура пояснительной записки

Пояснительная записка должна включать в себя следующие структурные части в указанной последовательности:

− титульный лист;

− задание на курсовую работу;

− содержание;

− введение;

− основную часть;

− заключение;

− перечень условных обозначений, символов, единиц и терминов (при необходимости);

− список использованных источников;

− приложения (при необходимости).

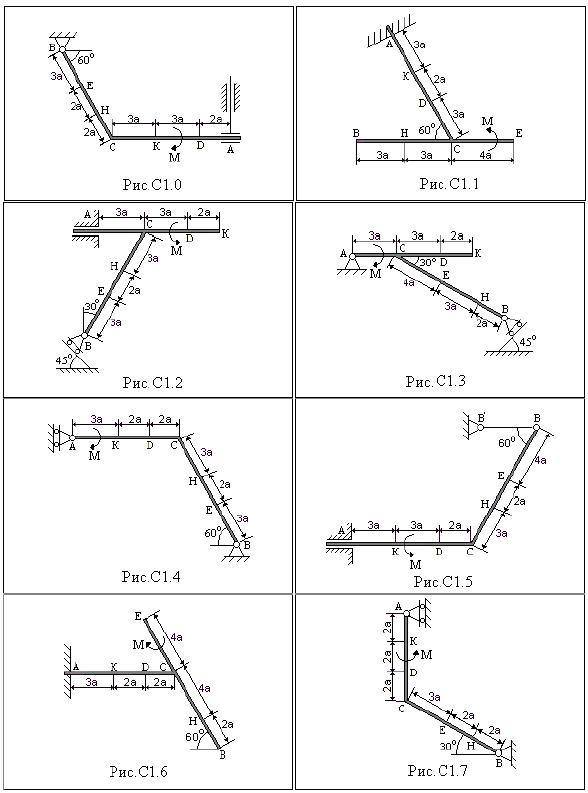
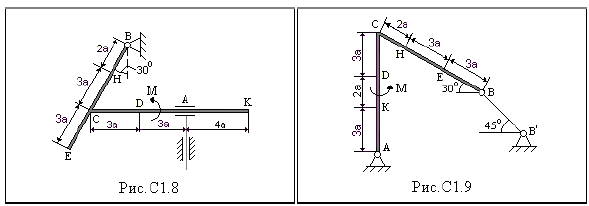
ЗАДАНИЕ на курсовую работу

СТАТИКА

Задание С1 Определение реакций опор балки

Конструкция, состоящая из двух прямолинейных стержней, жестко скрепленных между собой в точке С, расположена в вертикальной плоскости. На конструкцию действует пара сил с моментом М = 50 кН∙м, распределенная нагрузка интенсивности q = 10 кН/м и одна сосредоточенная сила. Величина этой силы, ее направление и точка приложения указаны в табл. С1. Там же в столбце «Нагруженный участок» указано, на каком участке действует распределенная нагрузка. Направление распределенной нагрузки на различных по расположению участках указано в табл. С1 А. При расчетах заданный на рисунках размер «а» принять равным 0,5 м.

Для данной конструкции

1. определить реакции связей конструкции для приведенных в условии данных;

2. выяснить:

− присутствует ли среди всех реакций связей конструкции реакция в виде момента пары сил, и, если такая реакция имеется, то выполнить пункт 3,

− если указанная реакция связи (в виде момента пары сил) отсутствует, то выяснить, в какой точке конструкции известно точное направление полной реакции связи в виде силы и для этой реакции выполнить пункт 4;

3. определить, при каком значении угла α_i (образуемого указанной в варианте задания сосредоточенной силой F_i с координатной осью) реакция в виде момента пары сил будет иметь по модулю минимальное или равное нулю значение, и для этого значения угла вычислить все реакции связей изучаемой конструкции;

4. определить, при каком значении угла α_i (образуемого указанной в варианте задания сосредоточенной силой F_i с координатной осью) выбранная полная реакции связи будет иметь по модулю минимальное или равное нулю значение, и для этого значения угла вычислить все реакции связей изучаемой конструкции.

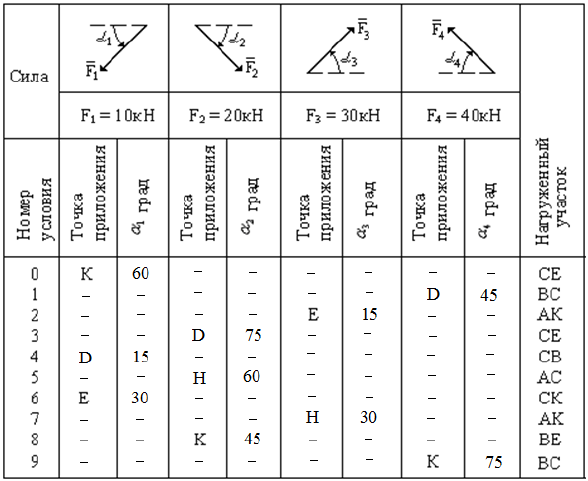
Таблица С1

Действующие нагрузки

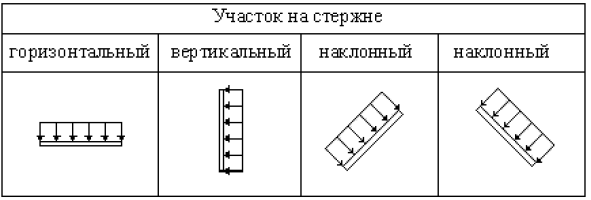
Таблица С1 А

Направление распределенной нагрузки

Указания. В задании С1рассматривается равновесие тела, находящегося под действием плоской произвольной системы сил. Составляя уравнения равновесия, следует учесть, что уравнение моментов сил будет более простым (содержать меньше неизвестных), если вычислять моменты относительно точки, в которой пересекаются  линии  действия  двух  неизвестных  реакций  связей. При вычислении моментов сил F часто удобно разложить их на составляющие F ' и F ", для которых плечи можно легко вычислить (эти составляющие могут быть, в частности, параллельны осям координат), и воспользоваться теоремой Вариньона, согласно которой М_О ( F ) = M_О ( F' ) + M_О ( F ").

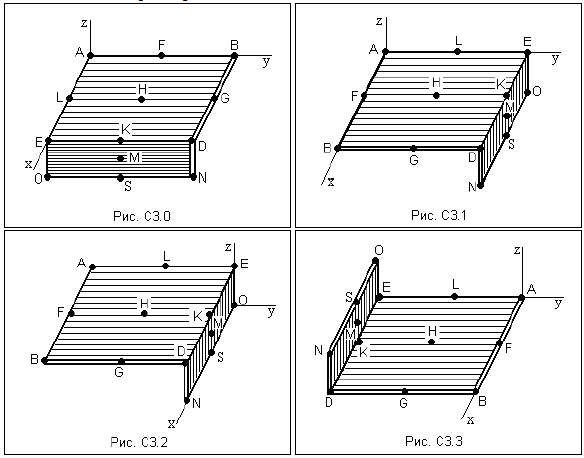
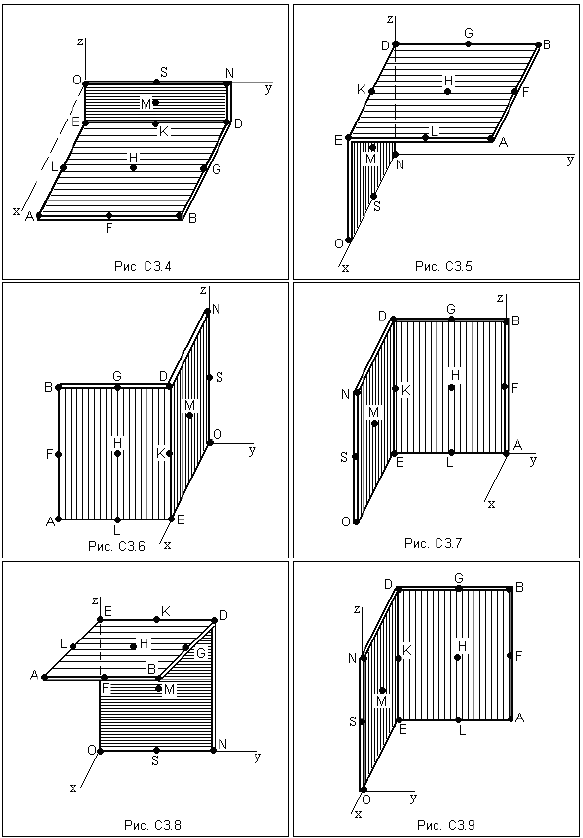
Задание С2 Определение координат центра тяжести тела

Две однородные прямоугольные пластины, приваренные под прямым углом друг к другу, образуют угольник. Размеры пластин в направлениях, параллельных координатным осям х, у, z, равны соответственно или 2ℓ , 3ℓ и ℓ на рис. С3.0 ÷ С3.4), или 2ℓ , 3ℓ и 4ℓ на рис. С3.5 ÷ С3.9. Силы тяжести большей и меньшей пластин на рис. С3.0 ÷ С3.4 соответственно равны 10 кН и 4 кН, для рис. С3.5 ÷ С3.9 силы тяжести пластин одинаковы и равны 8 кН. Каждая из пластин расположена параллельно одной из координатных плоскостей (плоскость хАу горизонтальна).

Из одной из пластин угольника вырезана фигура, расположение и вид которой указаны в таблице С2. Точки, обозначенные на рисунках, находятся по краям или в серединах сторон пластин.

Вычислить координаты центра тяжести угольника с вырезом для указанных на рисунках систем координат. При расчетах принять ℓ = 0,5 м. Толщиной пластин пренебречь.

Таблица С2

Указания

Решение задач на определение центра тяжести фигуры состоящей из плоских тел рекомендуется проводить в следующем порядке:

− исследуемую конструкцию разбить на части, для которых положение центра тяжести известно или его можно легко определить, например, на простейшие геометрические фигуры, при этом считать, что вырезанные из конструкции части (фигуры) обладают отрицательной площадью;

− определить площадь каждой части конструкции;

− найти координаты центров тяжести частей конструкции в выбранной системе координат;

− найденные значения подставить в формулы.

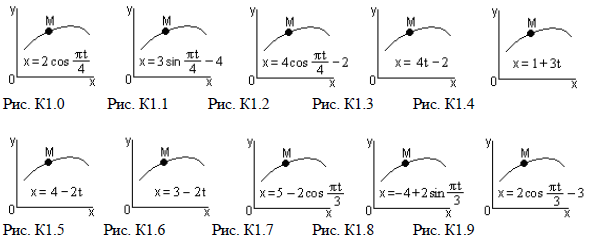
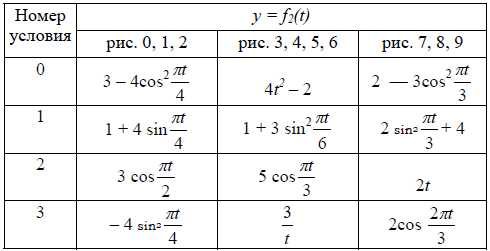
КИНЕМАТИКА

Задание К1. Определение кинематических характеристик движения материальной точки

По заданным уравнениям движения точки x = f₁(t), y = f₂(t) найти уравнение траектории ее движения, и для момента времени t₁ = 1с вычислить ее скорость, нормальное, касательное и полное ускорения, а также радиус кривизны траектории. На рисунке в масштабе изобразить траекторию движения точки и для заданного момента времени t₁ = 1с построить векторы скорости и ускорения.

Уравнения движения точки x = f₁(t) указаны на соответствующих рисунках, а уравнения движения y = f₂(t) приведены в табл. К1 (для рис. 0 –2 – в столбце 2, для рис. 3 − 6 − в столбце 3, для рис. 7 − 9 – в столбце 4); величины х и у измеряются в см, время в секундах (с).

Таблица К1

Уравнения движения точки y = f₂(t)

Указания. Перед выполнением задания К1 необходимо изучить темы:

−способы задания движения материальной точки;

−определение скорости и ускорения точки при различных способах задания движения,

а также познакомиться с порядком действий по определению  уравнения траектории точки и кинематических характеристик ее движения.

При решении задания целесообразно придерживаться следующего порядка действий:

− по возможности исключить из уравнений движения точки время и получить уравнение траектории движения точки (если это не удается сделать, то перейти ко второму пункту);

− построить траекторию движения точки;

− по уравнениям движения точки найти ее координаты для заданного момента времени t₁, проекции скорости и ускорения на оси координат, показать на чертеже положение точки и построить в соответствующих масштабах векторы скорости и ускорения;

− определить касательное и нормальное ускорения точки в данный момент времени и показать на чертеже разложение вектора полного ускорения точки на указанные составляющие;

− определить по направлениям векторов скорости и касательного ускорения точки, является ли ее движение в данный момент времени ускоренным или замедленным;

− найти радиус кривизны в соответствующей точке траектории.

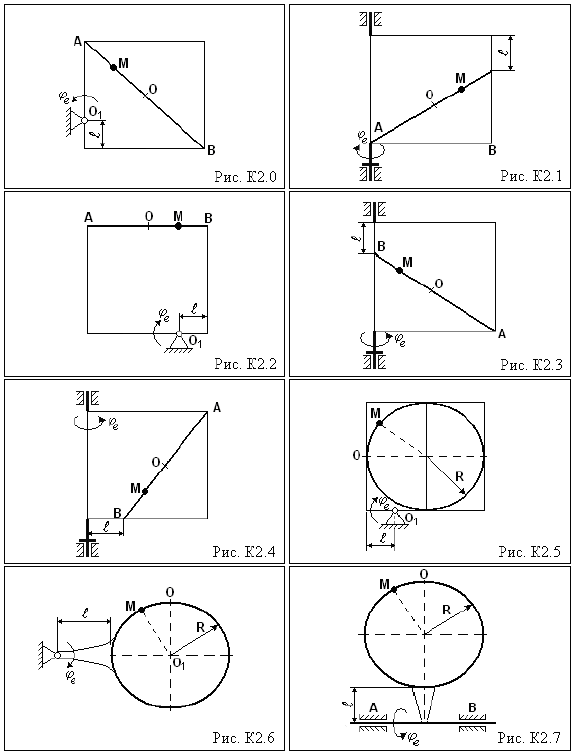
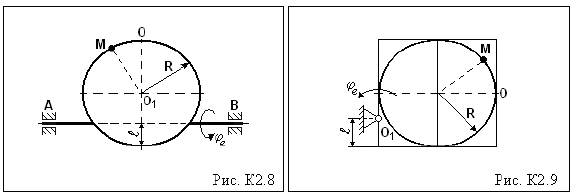
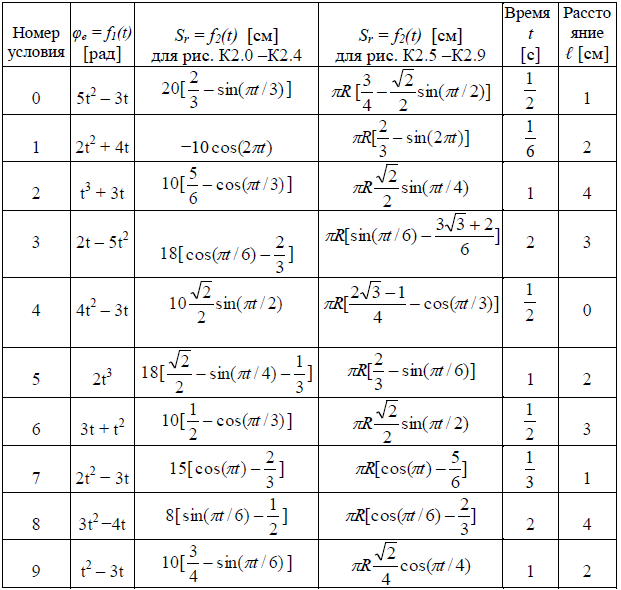
КИНЕМАТИКА

Задание К2 Изучение сложного движения материальной точки

Тело (квадрат со сторонами 10 см или диск радиуса R = 5 см) вращается вокруг неподвижной оси по закону φ_e = f₁(t). По желобу, имеющему прямолинейную форму или форму дуги окружности (на рисунках желоб выделен жирной линией), движется материальная точка М по закону ОМ = S_r = f₂(t).

На рисунках К2.0 – К2.4 точка О находится посередине прямой АВ, точка М показана в положении, при котором S_r > 0; положительное направление отсчета угла φ_e указано круговой стрелкой, расстояние ℓ задано в таблице в сантиметрах. Найти абсолютную скорость и абсолютное ускорение точки М для заданного момента времени   t = t₁. Данные для расчетов приведены в таблице К2.

Таблица К2

Исходные данные

Указания. Перед решением задания К2 необходимо изучить темы:

− кинематика материальной точки,

− простейшие виды движения твердых тел (поступательное движение и вращение вокруг неподвижной оси),

− сложное движение материальной точки,

а также овладеть методикой решения задач на сложное движение точки.

При решении задачи целесообразно придерживаться следующего порядка: – Разложить сложное движение точки на составляющие: относительное и

переносное движения.

–     Определить положение точки на движущемся теле в заданный момент времени (координаты точки в относительном движении); в случае, если траекторией относительного движения является окружность, положение точки определяется центральным углом φ = S_r/ R.

–  Движущуюся точку изобразить на рисунке в найденном положении.

–  Записать формулу для вычисления абсолютной скорости точки.

–   Записать формулы для вычисления относительной и переносной скоростей точки; вычислить их величины (модули) для заданного момента времени и показать векторы этих скоростей на рисунке.

–   Применяя теорему сложения скоростей, определить величину абсолютной скорости точки (при вычислениях использовать метод проекций векторов или теорему косинусов).

–  Записать формулу для вычисления абсолютного ускорения точки.

–     Записать формулы для вычисления составляющих относительного и переносного ускорений точки; вычислить их величины (модули) в данный момент времени и показать векторы составляющих ускорений на рисунке.

–    Вычислить величину ускорения Кориолиса в данный момент времени и показать направление вектора ускорения на рисунке.

–     Выбрать прямоугольную систему координат с началом в точке М, вычислить проекции на эти оси вектора абсолютного ускорения точки.

–   Применяя теорему сложения ускорений, определить величину абсолютного ускорения точки, используя метод проекций.

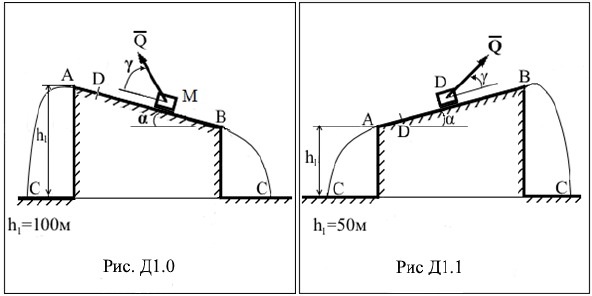
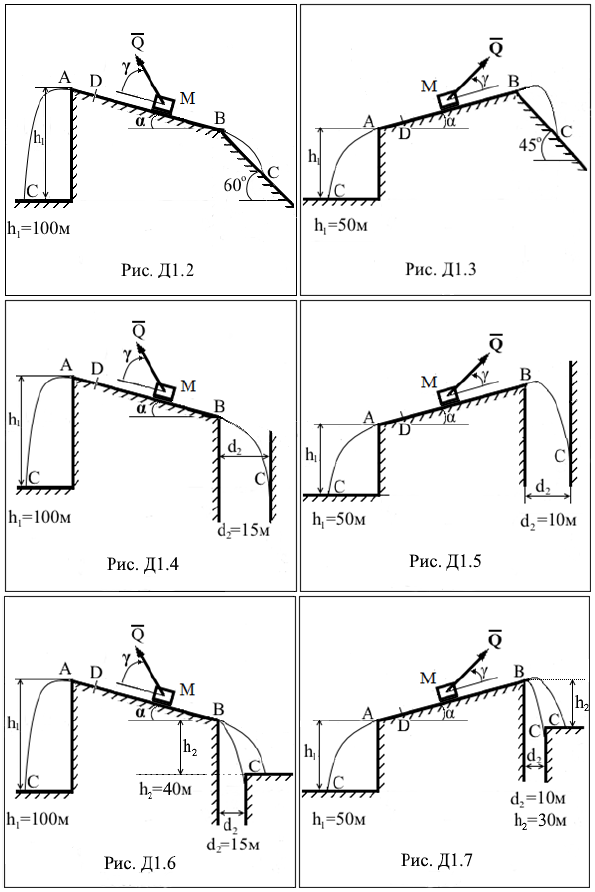
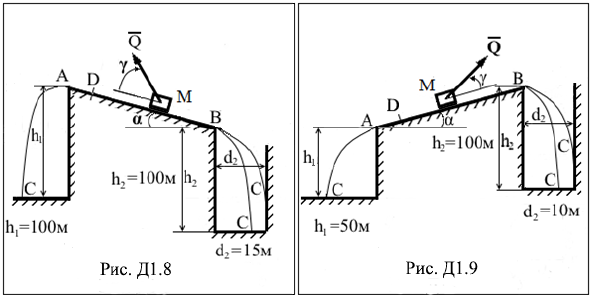
ДИНАМИКА

Задание Д1. Исследование движения материальной точки, находящейся под действием постоянных сил

Груз М массой m начинает движение из точки D с начальной скоростью V₀. Его движение происходит по наклонной плоскости длины ℓ, составляющей угол α с горизонтом вдоль линии АВ наибольшего ската. Положение точки D задается величиной AD = s₀, вектор V₀ направлен параллельно прямой АВ к точке В. При движении по плоскости на груз действует постоянная сила Q, направление которой задается углом γ, коэффициент трения скольжения между грузом и наклонной плоскостью равен f = 0,1. Через τ сек груз покидает плоскость или в точке А, или в точке В и, двигаясь далее в вертикальной плоскости под действием одной только силы тяжести, через T секунд после отделения от плоскости попадает в точку С. Все возможные варианты траекторий попадания груза в точку C показаны на рисунках.

Считая груз материальной точкой

1. определить:

– в какой точке (А или В) произойдет отрыв груза от плоскости,

– время τ движения груза по наклонной плоскости,

– скорость груза в момент отрыва,

– координаты точки С приземления груза,

– время T движения груза в воздухе,

– скорость груза в точке падения;

2. Построить (в масштабе):

− график траектории движения точки от точки D до точки С,

− график зависимости скорости точки от времени на участке АВ,

3. выяснить, существует ли возможность за счет изменения только величины начальной скорости добиться того, что груз покинет плоскость АВ в точке противоположной полученной по результатам расчетов в основном задании, если такая возможность существует, то привести условие, накладываемое на величину начальной скорости.

Необходимые данные приведены в табл. Д1 и на рисунках.

Таблица Д1

Указания. Задание Д1 ‒ на интегрирование дифференциальных уравнений движения точки (решение обратной задачи динамики материальной точки). Решение задачи разбивается на две части. Сначала следует рассмотреть движение груза на участке АВ, для чего составить и проинтегрировать дифференциальное уравнение движения точки. При этом необходимо определить, в какой из точек (А или В) груз оторвется от наклонной плоскости, и вычислить скорость отрыва. Затем следует рассмотреть криволинейное движение груза в зависимости от точки отрыва на участке ВС или АС, для чего составить и проинтегрировать дифференциальные уравнения движения точки в вертикальной плоскости. Полученные уравнения движения и уравнения скоростей используются для определения неизвестных характеристик криволинейного движения груза.

Примеры решения задач по этой теме можно найти в литературе [1], [5], [6].

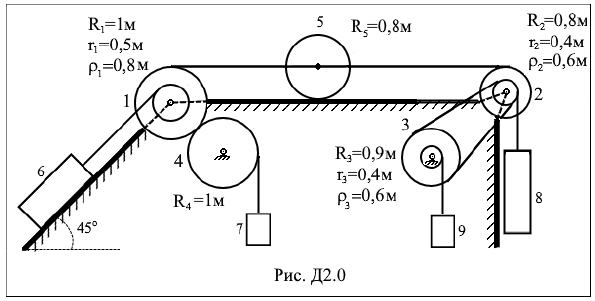
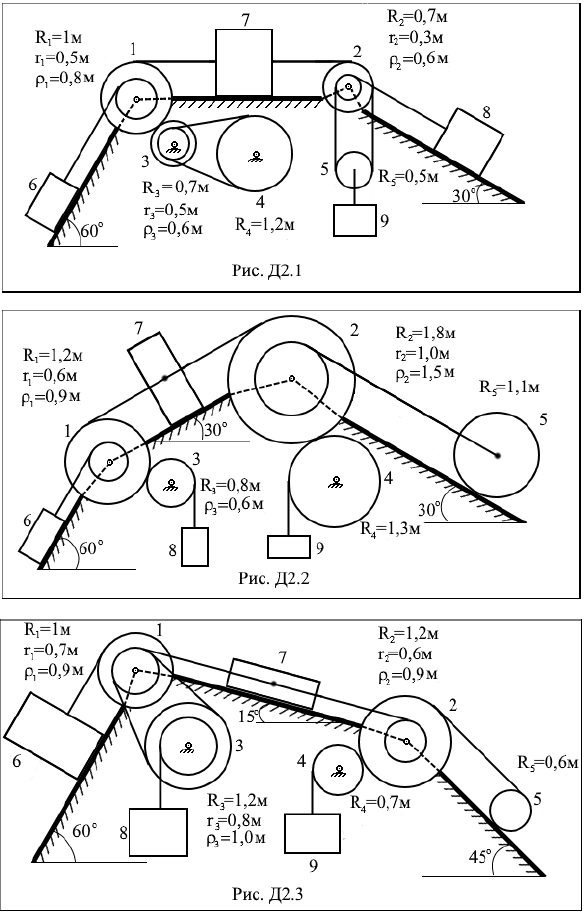
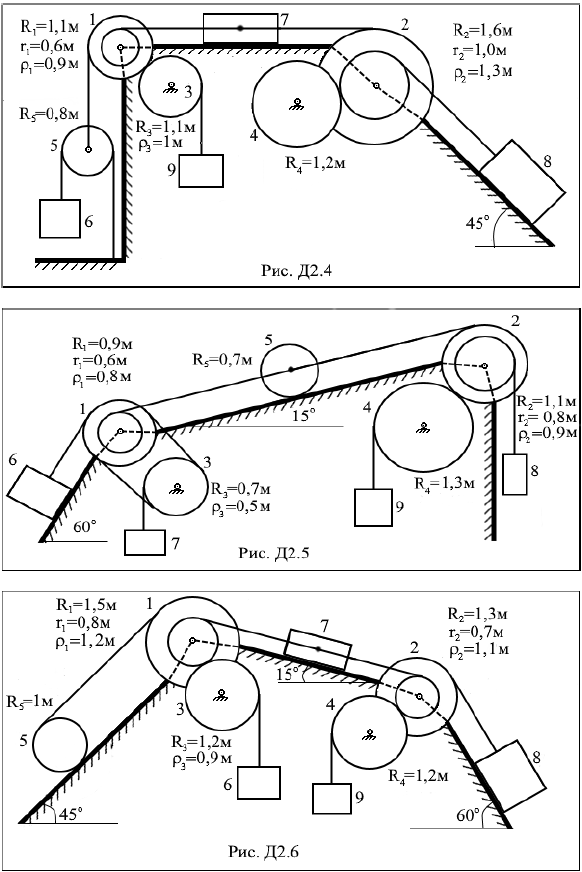
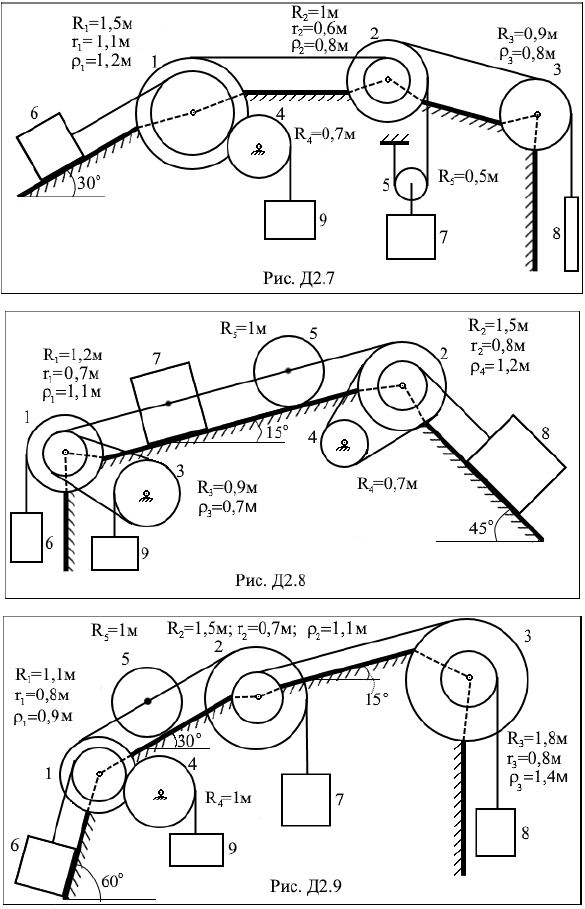
Задание Д2.  Применение теоремы об изменении кинетической энергии к изучению движения механической системы

Механическая система состоит из ступенчатых шкивов, колес, блоков 1÷5 и грузов 6 ÷ 9 (рис. Д2.0 ÷ Д2.9). На рисунках приняты обозначения: R_k – радиус внешней ступени шкива или радиус тела, r_k – радиус внутренней ступени шкива, ρ_k – радиус инерции тела относительно оси вращения. Для тел 1,2,3 заданы радиусы инерции ρ₁, ρ₂, ρ₃ относительно оси вращения, масса тела 4 равномерно распределена по внешнему ободу, тело 5 считать однородным цилиндром. Тела системы соединены друг с другом гибкими невесомыми нерастяжимыми нитями, которые или перекинуты через блоки, или намотаны на шкивы; участки нитей параллельны соответствующим плоскостям. Некоторые тела соединены ременными или фрикционными передачами.

Радиусы тел и радиусы инерции указаны на рис. Д2.0 ÷ Д2.9. Массы тел приведены в табл. Д2. Прочерк в таблице означает, что тело отсутствует и изображать его не надо. Если масса тела равна нулю, то данное тело показывается на рисунке, но его массой при расчетах следует пренебречь.

В некоторый момент времени под действием сил тяжести система приходит в движение из состояния покоя.

При скольжении по плоскостям на грузы действуют силы трения, коэффициент трения скольжения f равен 0,01. Качение всех тел происходит без скольжения; при этом для случая качения тел по неподвижным плоскостям следует учитывать трение качения, коэффициент трения качения δ = 1 см. Трением в осях вращения пренебречь. Длины нитей и длины участков достаточны для того, чтобы тела при движении не сталкивались друг с другом.

Определить скорость, указанную в табл. Д2 в столбце «Найти», после того как этот груз переместится на расстояние s = 10 м. При этом нужно указать, в какую сторону этот груз движется.

Таблица Д2

Исходные данные

Указания. Задача Д2 на применение теоремы об изменении кинетической энергии системы. При решении задачи учесть, что кинетическая энергия T системы равна сумме кинетических энергий всех входящих в систему тел; эту энергию нужно выразить через ту скорость, которую в задаче надо определить. При вычислении T для установления зависимости между скоростями точек тела, движущегося плоскопараллельно, или между его угловой скоростью и скоростью центра масс воспользоваться мгновенным центром скоростей. При вычислении работы сил надо все перемещения выразить через заданное перемещение s, учтя, что зависимость между перемещениями точек здесь будет такой же, как между соответствующими скоростями.