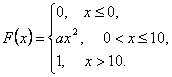Задание 1

В урне 30 шаров, из них 5 черных и остальные белые. Вынимаются один за другим 3 шара подряд. Какова вероятность того, что будет вынуто два белых и один черный шар?

Задание 11

На двух автоматах изготавливаются одинаковые детали. Производительность первого автомата в 2 раза больше, чем второго. Вероятность изготовления детали высшего качества на первом автомате – 0,95, а на втором – 0,97. Детали с обоих автоматов поступают вместе на склад. Определить вероятность того, что наудачу взятая со склада деталь окажется высшего качества.

Задание 21

Производится 3 независимых выстрела с вероятностью попадания 0,6 при каждом выстреле. X – число попаданий в мишень. Для случайной величины X построить ряд распределения, многоугольник распределения, функцию распределения. Найти математическое ожидание, среднее квадратичное отклонение.

Задание 31

Непрерывная случайная величина задана интегральной функцией распределения F(x):

Для этой случайной величины определить:

1) коэффициент a;

2) дифференциальную функцию f(x);

3) математическое ожидание, дисперсию, среднее квадратичное отклонение.

Построить графики f(x) и F(x).

Задание 41

Вычислить M(Z), если заданы законы распределения независимых случайных величин X и Y:

Z = 2X × 3Y.

Задание 51

Изделия, выпускаемые цехом, по своим линейным размерам распределяются по нормальному закону с математическим ожиданием a = 6 см и средним квадратичным отклонением s = 0,08 см. Какова вероятность того, что наудачу взятое изделие будет иметь размеры в пределах от 5,95 до 6,05 см?