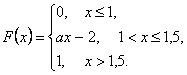Задание 3

Из десяти билетов лотереи выигрышными являются два. Определить вероятность того, что среди наудачу взятых пяти билетов хотя бы один выигрышный.

Задание 13

Имеются три одинаковые на вид урны: в первой урне – 3 белых и 4 черных, во второй – 2 белых и 2 черных, в третьей – 3 белых и 1 черный. Некто выбирает наугад одну из урн и вынимает из нее шар. Найти вероятность того, что извлеченный шар оказался белым.

Задание 23

Три стрелка стреляют по мишени. Вероятность попадания в мишень для первого стрелка равна 0,4; для второго – 0,45; для третьего – 0,6. каждый стрелок делает по одному выстрелу. X – число попаданий в мишень. Для случайной величины X построить ряд распределения, многоугольник распределения, функцию распределения. Найти математическое ожидание, среднее квадратичное отклонение.

Задание 33

Непрерывная случайная величина задана интегральной функцией распределения F(x):

Для этой случайной величины определить:

1) коэффициент a;

2) дифференциальную функцию f(x);

3) математическое ожидание, дисперсию, среднее квадратичное отклонение.

Построить графики f(x) и F(x).

Задание 43

Вычислить M(Z), если заданы законы распределения независимых случайных величин X и Y:

Z = X × 2Y – 1

Задание 53

Среднее число вызовов, поступающих на АТС за 1 мин., равно двум. Найти вероятность того, что за 3 мин. поступит 3 вызова, если число вызовов распределено по закону Пуассона.