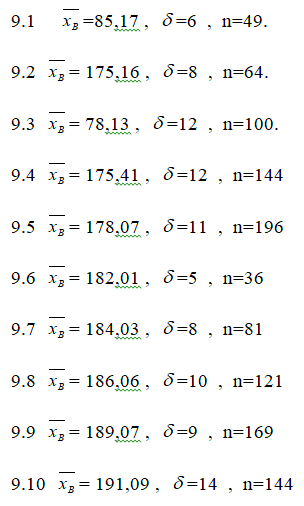Номер варианта – последняя цифра в номере зачётной книжки.

Задание 1

1.1 В коробке 6 одинаковых занумерованных шаров. Наудачу по одному извлекают все шары. Найти вероятность того, что номера извлечённых шаров появляются в возрастающем порядке.

1.2 В ящике 20 белых и 30 чёрных шаров. Наудачу взяли 10 шаров. Какова вероятность того, что среди них 6 белых шаров.

1.3 В ящике 10 белых и 10 чёрных шаров. Наудачу взяли 5 шаров. Какова вероятность того, что среди них 3 белых шаров.

1.4 В ящике 50 деталей, из которых 10 бракованных. Наудачу взяли 8 деталей. Какова вероятность того, что среди них 2 детали бракованные.

1.5 В ящике 20 деталей, из которых 12 стандартных. Из ящика взяли 6 деталей. Найти вероятность того, что из них 4 детали стандартные.

1.6 В урне 4 белых и 6 чёрных шаров. Из урны вынимают 2 шара. Найти вероятность того, что вынутые шары: а) одного цвета; б) разных цветов.

1.7 В урне 3 белых и 7 чёрных шаров. Из урны наудачу вынимают 2 шара. Какое событие более вероятно: а) шары одного цвета; б) шары разных цветов ?

1.8 В лотерее 10 билетов, из них 5 билетов выигрышных. Наудачу берётся 2 билета. Найти вероятность того, что среди них: а) оба билета выигрышные; б) хотя бы один билет выигрышный.

1.9 В ящике 10 деталей, среди которых 6 стандартных. Сборщик наудачу извлекает 3 детали. Найти вероятность того, что среди них: а) все 3 детали стандартные; б) хотя бы одна деталь стандартная.

1.10 Студент знает 40 из 50 вопросов программы. Найти вероятность того, что из двух содержащихся в экзаменационном билете вопросов студент знает: а) оба вопроса; б) хотя бы один вопрос.

Задание 2

2.1 Три станка работают независимо. Вероятность того, что в течении смены 1, 2, и 3-й станок выйдут из строя равны соответственно 0,05;  0,1;  0,15. Найти вероятность того, что за смену выйдет из строя только один станок.

2.2 В партии товаров товаровед отбирает бракованные изделия. Вероятность того, что наудачу взятое изделие окажется бракованным, равна 0,1. найти вероятность того, что из трёх взятых на проверку изделий одно бракованное.

2.3 Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого и 0,9 для второго сигнализатора. Найти вероятность того, что при аварии сработает: а) только один сигнализатор; б) хотя бы один сигнализатор.

2.4 Вероятность хотя бы одного попадания в цель при залпе из двух орудий равна 0,92. найти вероятность попадания в цель первым орудием, если вероятность попадания вторым орудием равна 0,8.

2.5 Два стрелка производят по одному выстрелу в мишень. Вероятность попадания в мишень первым стрелком равна 0,9; а вторым – 0,8. Найти вероятность того, что мишень поразит: а)только один стрелок; б) хотя бы один из стрелков.

2.6 В ящике 10 деталей, из которых 4 окрашенных. Сборщик наудачу взял 3 детали. Найти вероятность того, что среди них хотя бы одна деталь окрашена.

2.7 Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,6. Найти вероятность того, что из трёх взятых изделий два высшего сорта.

2.8 В ящике 40 деталей, из них 10 высшего сорта. Наудачу извлечены 2 детали. Найти вероятность того, что среди них высшего сорта: а) одна деталь; б) хотя бы одна деталь.

2.9 Вероятность того, что стандартная деталь находится в первом и втором ящиках, равна соответственно 0,6 и 0,8. Сборщик взял из  каждого ящика по одной детали. Какова вероятность того, что из них: а) одна деталь стандартная; б) хотя бы одна деталь стандартная.

2.10 В ящике 10 деталей, из них 6 высшего сорта. Сборщик наудачу взял 3 детали. Найти вероятность того, что среди них две детали высшего сорта.

Задание 3

3.1 В первой урне 3 белых и 5 чёрных шаров; во второй урне 6 белых и 4 чёрных шара. Из первой урны во вторую переложили один шар, а затем из второй урны взяли один   шар, который оказался белым. Найти вероятность того, что был переложен белый шар.

3.2 В двух ящиках содержится по 20 деталей, причём стандартных деталей в первом ящике 13, а во втором 18. из второго ящика извлечена одна деталь и переложена в первый ящик. После этого из первого ящика извлечена деталь, оказавшаяся стандартной. Найти вероятность того, что из второго ящика в первый была переложена стандартная деталь.

3.3 В ящике 50 деталей, из них 40 высшего сорта. Наудачу извлекается одна, а затем вторая деталь, оказавшаяся высшего сорта. Определить вероятность того, что и первая деталь была высшего сорта.

3.4 Сборщик получил две коробки одинаковых деталей, изготовленных заводом N1, и три коробки таких же деталей, изготовленных заводом N2. вероятность того, что деталь заводов N1 и N2 стандартная, равна соответственно 0,9 и 0,8. из наудачу взятой коробки сборщик взял деталь, которая оказалась стандартной. Определить вероятность того, что взятая деталь изготовлена заводом N1.

3.5 Два автомата производят детали, которые поступают на общий конвейер. Вероятность получения стандартной детали на первом автомате равна 0,95 ,  а на втором 0,8. Производительность  второго автомата вдвое больше, чем первого. Наудачу взятая с конвейера деталь оказалась стандартной. Найти вероятность того, что эта деталь изготовлена на первом автомате.

3.6 Сборщик получил 3 ящика деталей. В первом ящике 40 деталей, из них 20 высшего сорта, во втором 50 деталей из них 10 высшего сорта, в третьем 30 деталей из них 12 высшего сорта. Из наудачу взятого ящика извлечена деталь высшего сорта. Определить вероятность того, что эта деталь извлечена из 1-го ящика.

3.7 Имеется три ящика деталей, причём бракованных в 1-ом, 2-ом и 3-ем ящиках содержится соответственно 25%, 20%, 15%. Наудачу взятая деталь из наудачу взятого ящика оказалась бракованной. Найти вероятность того, что эта деталь извлечена из первого ящика.

3.8 Из ста деталей 60 первого, 30 второго и 10 третьего сорта. Вероятность брака среди деталей первого, второго и третьего сорта соответственно равна 0,01; 0,03 и 0,05. Наудачу взятая деталь оказалась небракованной. Найти вероятность того, что взятая деталь первого сорта.

3.9 Сборщик получил 100 деталей, из них 50 деталей изготовлено заводом N1, 30 деталей – заводом N2, 20 деталей – заводом N3.  Заводы N1, N2, N3 выпускают деталей отличного качества соответственно 70%, 80%, 90%. Наудачу взятая сборщиком деталь оказалась отличного качества. Найти вероятность того, что эта деталь изготовлена заводом N1.

3.10 По шоссе в среднем проезжает легковых машин вдвое больше, чем грузовых. Вероятность того, что легковая машина будет заправляться, равна 0,1; для грузовой машины эта вероятность равна 0,2. к бензоколонке подъехала для заправки машина. Найти вероятность того, что это легковая машина.

Задание 4

В задачах 4.1 – 4.10 требуется найти вероятность того, что в n  независимых испытаний событие появится не менее k раз, зная, что в каждом испытании вероятность появления события равна p.

4.1 n=4 ; k=2 ; p=0,1 .

4.2 n=5 ; k=2 ; p=0,2 .

4.3 n=6 ; k=2 ; p=0,3 .

4.4 n=5 ; k=2 ; p=0,4 .

4.5 n=6 ; k=3 ; p=0,5 .

4.6 n=4 ; k=3 ; p=0,6 .

4.7 n=5 ; k=3 ; p=0,7 .

4.8 n=6 ; k=4 ; p=0,8 .

4.9 n=5 ; k=4 ; p=0,9 .

4.10 n=5 ; k=3 ; p=0,1 .

Задание 5

В заданиях 5.1 – 5.10 требуется найти: а) математическое ожидание; б) дисперсию; в) среднее квадратическое отклонение дискретной случайной величины Х по закону её распределения, заданному рядом распределения ( в первой строке таблицы указаны возможные значения, во второй строке – вероятности возможных значений).

5.1

5.2

5.3

5.4

5.5

5.6

5.7

5.8

5.9

5.10

Задание 6

В задачах 6.1 – 6.10 случайна величина Х задана функций распределения F(x). Найти плотность распределения вероятностей, математическое ожидание, дисперсию случайной величины и построить графики f(x) и F(x).

Задача 7

Заданы математическое ожидание m и среднее квадратическое отклонение б нормально распределённой случайной величины.

Требуется найти: а) вероятность того, что X примет значение, принадлежащее интервалу (a, b);

б)  вероятность того, что абсолютная величина отклонения |X-m| окажется меньше положительного числа n.

7.1 m=10 ; б=4;  а=8; b=20;  n=8.

7.2 m=7 ; б=3;  а=3;  b=13;  n=6.

7.3 m=8 ; б=2;  а=4;  b=14;  n=6.

7.4 m=9 ; б=5;  а=5;  b=15;  n=8.

7.5 m=10 ; б=4;  а=6;  b=16;  n=10.

7.6 m=11 ; б=3;  а=7;  b=17;  n=6.

7.7 m=12 ; б=5;  а=8;  b=17;  n=10.

7.8 m=13 ; б=3;  а=9;  b=19;  n=4.

7.9 m=14 ; б=4;  а=10;  b=20;  n=10.

7.10 m=15 ; б=5;  а=11;  b=21;  n=6.

Задача 8

Дано статистическое распределение выборки (в первой строке указаны выборочные варианты x_i  , а во второй строке – соответствующие частоты ).

Требуется:

1) Построить полигон частот.

2) Найти выборочную среднюю x_в (несмещённую оценку средней)

3) Найти выборочную дисперсию (смещённую оценку).

4) «Исправленную» выборочную дисперсию S² (несмещённую оценку) и «исправленное» среднее квадратическое  отклонение S.

Задача 9

Найти доверительные интервалы для оценки математического ожидания с надёжностью y=0,95, зная выборочную среднюю, объём выборки n и среднее квадратическое отклонение нормально распределённой величины X.