| Общая информация » Каталог студенческих работ » ВЫСШАЯ МАТЕМАТИКА » ТюмГАСУ, высшая математика |
| 08.12.2010, 12:17 | |||||||||||||||||
Контрольная работа №4 Интегрирование функций Задача 157 Требуется найти интегралы. В пунктах а) и б) сделать проверку.
Задача 167 Требуется вычислить площадь области, ограниченной линиями. Сделать чертеж.
Задача 177 Вычислить
длину дуги кривой Задача 187 Требуется вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и чертеж его проекции на плоскость xOy.
Задача 197 Найти момент
инерции однородного тела, ограниченного параболоидом вращения Контрольная работа №5 Дифференциальные уравнения Задача 207 Требуется найти общее решение дифференциального уравнения первого порядка:
Задача 217 Требуется
найти частное решение дифференциального уравнения второго порядка Задача 227 Требуется найти общее решение линейного дифференциального уравнения второго порядка с постоянными коэффициентами:
Задача 237 Требуется найти общее решение системы дифференциальных уравнений методом исключения:
Задача 247 Найти уравнение кривой, проходящей через точку (1, 0) и обладающей тем свойством, что отрезок, отсекаемый касательной на оси Oy, равен полярному радиусу точки касания. Контрольная работа №6 Теория вероятностей и элементы
математической статистики Задача 257 Два студента вместе выполняют работу по черчению. Студент А при выполнении работы допускает 3% ошибок, студент В – 6%. Студент А выполнил 4 чертежа, студент В – 3 чертежа. Наудачу взятый чертеж выполнен с ошибкой. Что вероятнее: чертеж выполнен студентом А или В? Задача 267 В мастерской работают 6 механизмов. Для каждого механизма вероятность перегрева мотора к обеденному перерыву равна 0,8. Найти вероятность того, что к обеденному перерыву а) перегреются моторы у четырех механизмов; б) перегреются моторы не более, чем у двух механизмов; в) ни у одного механизма мотор не перегреется. Задача 277 Непрерывная случайная величина задана интегральной функцией
распределения F(x):
Требуется найти: 1) дифференциальную функцию f(x) (плотность вероятности); 2) математическое ожидание M(X); 3) дисперсию D(X) и среднее квадратическое отклонение s(X); 4) вероятность попадания заданной случайной величины X в интервал P(2<x<2,5). Задача 287 Требуется найти вероятность попадания в интервал (3, 7)
нормально распределенной случайно величины X, если известны ее математическое ожидание a = 4 и среднее
квадратическое отклонение s
= 3. Задача 297 Требуется найти доверительный интервал для оценки
математического ожидания a нормального распределения с надежностью g = 0,99, зная выборочную среднюю xв = 188,07, среднее квадратическое отклонение s = 11 и объем выборки n = 121. Задача 307 Из генеральной совокупности произведена выборка. Данные
наблюдений сведены в группы и представлены в виде таблицы: первая строка –
середины частичных интервалов xi, вторая строка – соответствующие им частоты ni.
Требуется провести статистическую обработку экспериментальных данных по следующей схеме: 1. Построить выборочную (эмпирическую) функцию распределения. 2. Построить гистограмму относительных частот. 3. Вычислить
числовые характеристики выборки: выборочную среднюю xв,
выборочное среднее квадратическое отклонение sв, исправленное
среднее квадратическое отклонение Sв. 4. Считая, что данная выборка принадлежит нормальной
совокупности, записать уравнение выравнивающей (теоретической) кривой и,
вычислив теоретические частоты, построить ее на одном чертеже с полигоном
частот (эмпирической кривой). 5. Проверить для заданного уровня значимости a = 0,05 по критерию согласия Пирсона гипотезу о нормальном
распределении генеральной совокупности. 6. В случае принятия гипотезы найти с надежностью
(доверительной вероятностью) g
= 0,95 интервальные оценки параметров генеральной совокупности, т.е.
доверительные интервалы математического ожидания a и среднего квадратического отклонения s, применяя распределение Стьюдента и c2(«хи квадрат»). | |||||||||||||||||

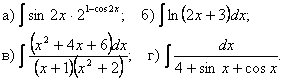
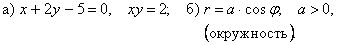
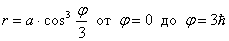 .
.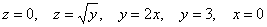 .
.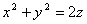
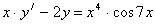 .
.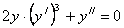 , удовлетворяющее условиям
, удовлетворяющее условиям 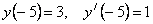 .
.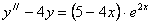 .
.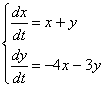 .
.