1. Элементы линейной алгебры

Задание 9

Даны матрицы:

.

Найти матрицу  и вычислить ее определитель.

Задание 19

Найти матрицу, обратную данной. Сделать проверку.

.

Задание 29

Решить систему линейных уравнений тремя способами: по формулам Крамера, матричным методом и методом последовательного исключения неизвестных (методом Гаусса).

2. Аналитическая геометрия на плоскости

Задание 39

Через точку М(2,2) провести прямые: параллельно, перпендикулярно и под углом 45⁰ к прямой L: x + 4y + 4 = 0. Сделать чертеж.

Задание 49

В треугольнике ABC известны координаты его вершин: A(3;8), B(4;1), C(-6;-4). Найти уравнения стороны AC; высоты и медианы, проведенных из вершины B; длину этой высоты; угол A. Сделать чертеж.

Задание 59

Построить на плоскости область решений системы линейных неравенств:

Задание 69

Определить тип кривой, привести уравнение к каноническому виду, кривую построить.

а) x² – 4y² – 16 = 0,

б) x² + y² – 6x – 7 = 0.

3. Векторная алгебра. Аналитическая геометрия в пространстве

Задание 79

Убедиться, что векторы  не лежат в одной плоскости, написать разложение вектора  по векторам .

Задание 89

Точки A₁(0;0;0), A₂(-3;0;-4), A₃(4;0;-3), A₄(1;5;-3) являются вершинами пирамиды. Вычислить: 1) длину ребра А₁А₂; 2) угол между ребрами А₁А₂ и А₃А₂; 3) площадь грани А₂А₃А₄; 4) объем пирамиды; 5) уравнение прямой А₁А₃; 6) уравнение плоскости А₂А₃А₄; 7) уравнение высоты, опущенной из вершины А₁ на грань А₂А₃А₄; 8) длину этой высоты. Сделать чертеж.

4. Комплексные числа

Задание 99

Даны комплексные числа  в алгебраической форме.

1. Записать их в тригонометрической и показательной формах, изобразить на комплексной плоскости.

2. Выполнить указанные действия: z₁ + z₂, z₁ ∙ z₂, z₂ : z₁; .

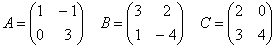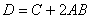
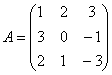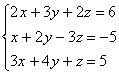
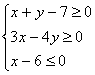
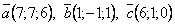
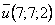
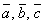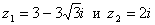
3. Найти все корни уравнения 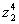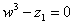, изобразить их на плоскости.