| Общая информация » Каталог студенческих работ » ВЫСШАЯ МАТЕМАТИКА » ТюмГСХА, высшая математика |
| 05.12.2010, 22:39 | |
Контрольная работа №1 Задание 2 Решить заданную систему уравнений, пользуясь формулами Крамера. Сделать проверку полученного решения.
Задание 12 Даны координаты вершин треугольника АВС. А(0; -1), В(3; 3), С(4; 1). Найти: 1) Длину стороны АВ; 2) уравнения сторон АВ и ВС и их угловые коэффициенты; 3) внутренний угол В в радианах с точностью до 0,01; 4) уравнение медианы АЕ; 5) уравнение и длину высоты CD: 6) уравнение прямой, проходящей через точку Е параллельно стороне АВ. Задание 22 Даны координаты вершин пирамиды ABCD. А(2; 3; 2), В(0; 6; 2), С(0; 3; 8), D(2; 6; 10). Требуется: 1. записать
векторы 2. найти угол
между векторами 3. найти
проекцию вектора 4. найти площадь грани АВС; 5. найти объем пирамиды ABCD. Задание 32 Найти указанные пределы: 1) 2) Задание 42 Найти
производные а) в) Задание 52 а) б) 1) Исследовать данные функции методами дифференциального исчисления и начертить их графики. 2) Для функции из пункта а) найти дополнительно наибольшее и наименьшее значения на отрезке [a; b]. Задание 62 Проволока длиной 40 см согнута в прямоугольник. Каковы должны быть размеры этого прямоугольника, чтобы площадь его была наибольшей? Задание 72 Найти
приближенное значение функции Задание 82 Для кривой Контрольная работа №2 Задание 92 Найти неопределенный интеграл способом подстановки (методом замены переменной):
Задание 102 Найти неопределенный интеграл, применяя метод интегрирования по частям:
Задание 112 Найти неопределенный интеграл, пользуясь разложением рациональной дроби на простейшие:
Задание 122 Вычислить определенный интеграл:
Задание 132 Вычислить площадь, ограниченную заданными параболами:
Задание 142 Найти длину дуги кривой:
Задание 152 Вычислить несобственный интеграл или установить его расходимость:
Задание 162 Вычислить частные производные первого и второго порядка заданной функции:
Задание 172 Задана функция z = f(x, y). Найти градиент и производную этой функции в заданной точке M(x0, y0) в направлении вектора l, составляющего угол a с положительным направлением оси OX.
Задание 182 Найти экстремум заданной функции:
Задание 192 С помощью двойного интеграла вычислить координаты центра тяжести фигуры, ограниченной заданными линиями (поверхностную плотность считать равной единице):
Задание 202 Вычислить
работу, совершаемую переменной силой | |

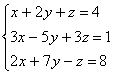
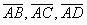
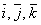
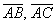 ;
;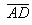
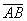 ;
;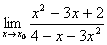
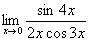 .
.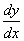 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.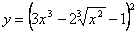 ,
,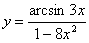 ,
,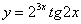 ,
,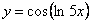 .
.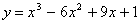 ;
; 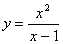 .
.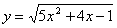 ,
, 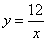
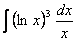 .
.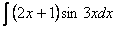 .
.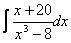 .
.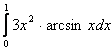 .
.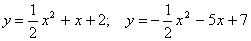 .
.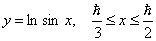 .
.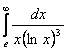 .
.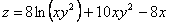 .
.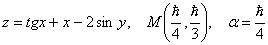 .
.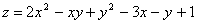 .
.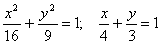 .
.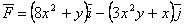
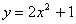 , соединяющем точки
, соединяющем точки 